基于生本理念的初中数学概念教学探索

自“生本理念”推行以来，笔者反复开展了实践研究，对数学概念课的教学模式进行了反复试验与矫正，取得了一定的进展.下面以“随机事件与概率”的教学为例给出基于“生本理念”的概念教学实践.

1 教学环节1：复习旧知，感知新知

问题1一次国际乒乓球单打比赛中，甲、乙两名选手进入最终决赛，值得欣喜的是这两名选手都是中国选手.现在有几个问题想考考大家，第一个问题是，这项比赛中冠军会是中国选手吗？

生（积极回答）：是.

师（继续提问）：冠军会是外国选手吗？

生（积极回答）：不会.

师（继续提问）：冠军是选手甲吗？

学生（思考后回答）：不确定，有可能是选手甲，也有可能是选手乙.

说明：旧知是新知的基础，新知又是旧知的引申.在课堂导入环节，笔者引导学生在回顾旧知的同时自然而然地进入到新知的探索中去.教师总结这三个问题的回答过程，强调逻辑推理和分析能力在数学学习和实际问题解决中的重要性.

2 教学环节2：自主探究，获取概念

问题2想一想，填一填：

（1）问题1中“冠军是中国选手”，属于什么事件？

（2）问题1中“冠军是外国选手”，属于什么事件？

（3）问题1中“冠军是中国选手甲”，属于什么事件？

师（学生分组讨论后）：第一组同学，请分享你们对第（1）问的推理过程.

生1：因为甲和乙都是中国选手，所以无论谁赢，冠军一定是中国选手.我们认为这属于必然事件.

师：很好，你们确实理解了这个逻辑.那么谁能告诉我为什么这是必然事件？

生2：因为所有可能的冠军（甲或乙）都是中国人，所以冠军必然是中国的.

师：完全正确.这就是必然事件的定义——在一定条件下一定会发生的事件.接下来，第二组同学，你们对等（2）问的推理是怎样的？

生3：因为决赛选手都是中国选手，所以冠军不可能是外国选手.我们认为这属于不可能事件.

师：很好.你们准确地识别出了这是一个不可能事件.谁能解释一下为什么？

生4：因为没有外国选手参与比赛，所以冠军不可能是外国选手.

师：完全正确.不可能事件是指在一定条件下一定不会发生的事件.现在，第三组同学，你们是如何推理第（3）问的？

生5：比赛结果不确定，冠军可能是甲，也可能是乙.我们认为这是随机事件.

师：很棒.你们正确地识别出了这是一个随机事件.谁能解释一下随机事件的特点？

生6：随机事件是指在一定条件下，可能发生也可能不发生的事件.它的结果是不确定的.

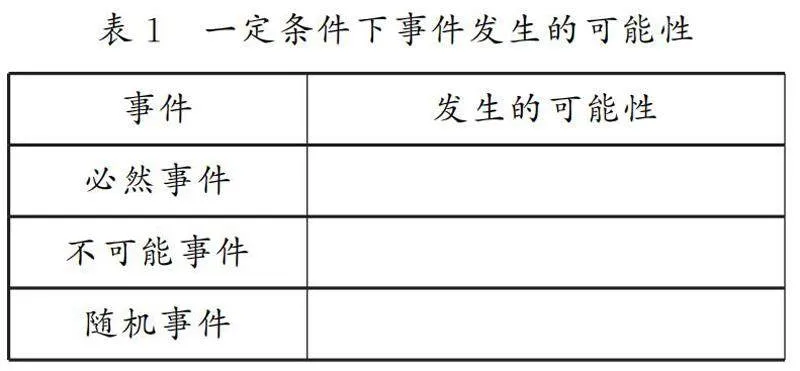
师：非常好！随机事件的特点就是它的结果是不确定的.通过今天的讨论，我们加深了对必然事件、不可能事件和随机事件的理解.请大家根据刚才讨论的内容，试着填写表1.

学生根据所学内容完成表1后，教师进行总结并展示答案.

问题3先独立思考并尝试列举必然事件、不可能事件和随机事件的例子，然后小组合作讨论，最终以小组为单位各派一名代表进行全班交流.

说明：笔者抓住学生对“可能性”的认识逐步延展开去，理解概念、归纳概念、分类和识别事件、举例强化，一步步地让模糊的概念变得清晰起来，最终在识别和例举中强化认识，形成清晰的概念框架.

3 教学环节3：适切追问，无痕建构

问题4一个不透明纸箱内放有4个除颜色外完全相同的小球，其中3个红色，1个白色.那么，从纸箱内任意摸出1个球，它可能是什么颜色？任意摸出1个球时，红球与白球的可能性是否相同？若不相同，你觉得哪种事件发生的可能性更大？为什么？

师：任意摸出1个球，可能是什么颜色呢？

生：红色或白色.

师：那摸出红球的可能性与摸出白球的可能性一样吗？

生：应该不一样吧，红球3个，白球1个，红球比白球多，摸到红球的可能性大.

师：有道理.该怎么证明呢？

生：可以做实验.

师：很好，请大家分组做实验并记录摸出红球和白球的次数.

学生开始分组做实验.

师：大家观察下自己的实验结果，是不是摸出红球的次数比白球多呢？

生：是的.

师：该怎么用数值表示这个可能性呢？

学生思考并讨论，但没有新结果.

师：如果是红、黄、蓝、绿4个不同颜色的小球，那么摸到红色小球的可能性用数值怎么表示呢？

生：1/4.

师：非常好！摸到红球的可能性是1/4.

说明：在学生思维的最近发展区追问“可能性的大小及如何用数值表示”，让学生通过深度思考与探究切实理解每个球被摸到的可能性，从而无痕引出概率的概念，为后续的深度探究打基础.

问题5想一想，说一说：

（1）我们发现，问题4的探究中得到红球的可能性可以用数值来表示，这就是概率，请试着描述概率的定义；

（2）还是从问题4中不透明纸箱中任意摸出1个球，摸到白球的概率是多少？

（3）还有一个不透明纸箱，其中装有4个完全一样的白球，那摸到白球的概率是多少？摸到红球的概率呢？

（4）基于以上研究，你认为三类事件发生的概率取值范围是多少？

教师依次引导学生回答第（1）（2）（3）（4）问，从概率的定义到概率的计算逐步深入，进一步明晰本节课所学内容和深化理解本节课知识.具体过程略.

说明：先让学生用数值去描述可能性的大小，再抛出问题不断设问，其目的就是让学生循着之前的探究路径感知和体验知识间的联系，从而深化对概念本质的理解和认识.

4 环节4：变式探究，有效提升

问题6有一枚质地均匀的骰子，小红随意将其掷出，求以下各种事件的概率：

（1）向上一面的点数是2；

（2）向上一面的点数是奇数；

（3）向上一面的点数比2大且比5小.

变式以小组为单位试着为问题6设计一个概率问题.

学生分组讨论并根据实际情境设计概率问题.

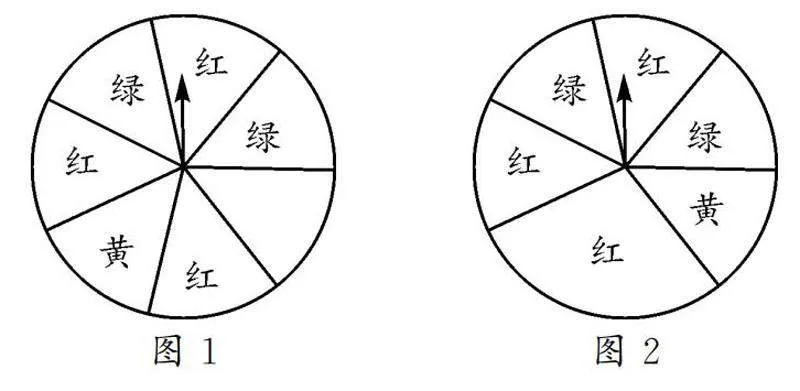
问题7图1是一个分为7个相同扇形、可自由转动且指针固定的转盘，共有红、黄、绿三种颜色，转动转盘后待它自由停止，指针会指向某个扇形所在区域（当指针指向交线则默认指向右边扇形）.

（1）指向红色的概率是多少？

（2）指向红色或黄色的概率是多少？

（3）不指向红色的概率又是多少？

变式将问题7中的转盘换成图2所示的转盘，其他条件和问题均不改变，请回答上述问题.

学生根据所学知识思考后回答问题.

说明：笔者通过改编教材例题并设计变式，深化学生的理解与认识，同时促进学生对概念的深刻理解.

5 环节5：整合梳理，深化认识

教师带领学生梳理单元知识并在黑板上书写本课知识结构图（图略）.

说明：在梳理知识结构图的过程中，每个学生都能积极参与，使得不同的学生得到不同的发展，真正落实了“以生为本”的教学理念.

总之，“生本理念”为我们的课堂教学提供了“取之不尽用之不竭”的教学资源.教学时应充分发挥引导作用，用巧妙的提问引导学生思考和探究，进而提升学生的数学核心素养，让“生本课堂”成为数学课堂的常态.