初中数学“深度学习”教学探索

摘要：“深度”是数学教学的应然追求，更是数学学习的自然选择.“深度学习”呼唤知识与学习层面上的双重深度，注重提升学生学习的主动性、创新能力和学科素养.数学深度学习，要从深度思考开始、从深度合作出发、从深度体验展开，数学深度学习呼唤教师的深度探索，培养和发展学生的数学核心素养.

关键词：深度学习；深度思考；深度合作；深度体验

在数学教学领域，“深度学习”不仅是一种教学理念，更是一种教学方式，就是关注到学习者深入思考、自主学习及问题内在意义的发掘，它主要倡导通过深度挖掘教学内容本身，以趣味性、挑战性、创造性的教学方式激发学习者的学习潜能，建构知识体系，促成全面而深入的理解，进而培养学生的数学思维、创新能力及关键性能力[1].毋庸置疑，深度学习确实能让学生深入理解和掌握、深入思考和反思、长期记忆和迁移.但在实际教学实践中，笔者发现仍旧存在一些仅仅是知识层面上的深度，而并无学习层面上的，使得学生的学习被动化、虚浮化.基于此，“深度学习”呼唤知识与学习层面上的双重深度，注重提升学生学习的主动性、创新能力和学科素养.

1 深度学习，从深度思考开始

对于深度学习而言，深度思考是出发点，也是根本所在.大量教学实践表明，优化问题设计，可以极好地诱发学生的深度思考，达成对知识的深层次理解，促成深度学习，在提高教学效率的同时培养数学核心素养.那么教师就需精巧设计问题，以问题引领学生主动思考、积极探究，以经历深度思考，促成深度学习.

案例1以分式教学中“分式无意义条件”的探索为例

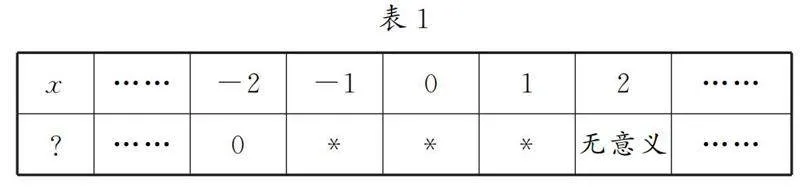
问题1细致观察表格（表略）中的数据，并说说你的发现.

教师给足学生填写与思考的时空，学生自主自发地展开了讨论，很快有学生提出“其中有一空不能填”的质疑，并逐渐发散开去，大部分学生开始质疑题目出错.

点拨1：为什么不能填？具体分析一下！（当a=1时就出现了分母为0的情形，那就“无意义”了.）

点拨2：那我们何不填上无意义呢？

评析：此处的填表，教师没有反复强调，也没有让学生逐一阐述，而是展示算出的答案，即将活生生的数据展示出来，让学生经历活生生的数学思考过程.在这个过程中，学生产生质疑，并主动说出“无意义”的想法，学生的思考淋漓尽致，这样的深度学习是实实在在的，从而流畅而快速地实现了自然建构.

问题2如表1所示，这里的“？”所表示的代数式是什么？（问题抛出后，学生陷入沉思，很快有了如下发现：当x=－2时，代数式的值是0，因此其分子是x+2.）

追问1：那该代数式的分母呢？（有学生不假思索地说出“任意数或任意整式”，大部分学生表示赞同，但也有少数学生默不作声，陷入沉思.）

追问2：有没有不同想法？（当x=2时代数式的值无意义，由此可见该代数式的分母应是x－2.）

追问3：只能是x－2？（学生又思考片刻，又有学生给出结论“还可以是2－x”.）

…………

优化的问题引领可以自主诱发学生的深度思考，这一点在上述案例中体现得淋漓尽致.教师层层递进地抛出问题，有效打破了学生的思维定式，促使思考不断深入，从而使学生对知识本质有了全面而深入的理解，使学生的批判性思维和创新思维得以形成.当然，除去优化问题设计，还需给予学生充足的思考时空，让学生去深度思考、深度探究、深度交流，如此，才能促成真正意义上的深度学习.否则，我们在数学学习中就会只获得深度学习的“形”，而没有获得深度学习的“神”.

2 深度学习，从深度合作出发

深度合作助推深度学习走向深处，数学深度学习必须从学生的深度合作出发.在教学中，笔者发现，许多教师也研究教材、学生和教学来设计合作性学习活动，但由于研究的深度不够或方向有所偏颇，从而导致合作学习缺乏实效性和针对性.笔者认为，深度合作应当从具体学情出发，研究学生、教学内容和数学本身，科学组建合作小组，让学生对核心问题进行深入探讨，加深思考深度，从而提高深度合作的有效性.只有这样，教师才能用深度合作引导学生的数学发现，促成深度学习，培养学生的数学核心素养.

案例2以“全等三角形的判断”教学为例

核心问题：一个三角形有几个元素？完全确定一个三角形的形状及大小，需要确定其中的几个元素？

数学探究1：只给出2个元素，所画的三角形的形状、大小确定吗？

（1）△ABC的两边长分别为3 cm，4 cm；

（2）△ABC的两个内角分别为45°，60°；

（3）△ABC的一边长是4 cm，一个内角是45°.

数学探究2：给出如下条件，你能画出确定大小与形状的三角形吗？

（1）试画出△ABC，其中AB=3 cm，AC=2 cm，BC=4 cm；

（2）试画出△ABC，其中BC=4 cm，∠B=50°，∠C=70°；

（3）试画出△ABC，其中AB=3 cm，∠B=50°，∠C=70°；

（4）试画出△ABC，其中∠A=45°，AB=3 cm，AC=2 cm；

（5）试画出△ABC，其中∠A=45°，AB=3 cm，BC=2.5 cm.

数学探究3：通过对上述探究的观察与讨论，你觉得完全确定一个三角形的关键是什么？

数学探究4：经过合作探讨，我们清楚知道3个元素不一定可以确定一个三角形，那4个元素呢？

为了培养有智慧、有素养的学生，深度合作具有广阔的前景.深度合作的成功常常源于教师在课前能设计良好的合作环境和精准的探究问题，给学生以智慧的熏陶，在课中能做好现场调适，推动学生思考的深入，让学生在深度合作中有效体验、自主建构、发展思维[2].以上案例中，教师的巧妙设计引导学生人人参与、深度思考、自主探究、合作交流、数学分类、数学表达，实现沟通交流、数学能力、推理论证等素养上的不断飞跃，让数学深度学习事半功倍.

3 深度学习，从深度体验展开

体验是数学学习的常态，深度体验是深度学习的常态.可以这样说，没有深度体验的深度学习是无效或者低效的.只有学生真正意义上感知了、经历了、体验了，数学学习才能达到一定深度；只有经历了深度体验的过程，一切外在学习因素才能共同协作，形成具有生命力的深度学习.因此，数学深度学习，必须从学生的深度体验展开.

案例3以“反比例函数的图象与性质”教学为例

数学探究：你能类比正比例函数y=6x图象的作图步骤，试着作出反比例函数的图象吗？在作图过程中，体会列表、描点、连线等过程.

上述探究活动的开展主要是为了让学生在列表、描点、连线的过程中深度体验，形成对反比例函数性质的深刻理解与认识，从而为后续重点、难点的突破做足铺垫.在学生深度探究的过程中，教师发挥教学机智适时引导.例如，在列表时启发学生自主思考“自变量该如何取值”.又如，为了让学生切实体会“折线并非反比例函数图象”，教师利用几何画板制作了一个折线形状的图象，将其巧妙融入坐标系中，使学生自然生成“反比例函数图象必须是平滑曲线”的认识.这样的探究过程中，学生的体验是深刻的，有了这样深刻的体验，学生建构反比例函数的性质也就水到渠成了.

总之，数学深度学习从本质上来说并非仅仅是学生学习的深度，更在于教师教学的深度，唯有深入钻研、细致设计、巧妙安排，才能让学生的深度学习真正具有深度.在数学教学中，当教师巧妙创设情境引发学生的深度思考时，当教师直面研究课题和具体学生设计探究活动来引导学生深度合作时，当教师意识到“以学生的学”为根本来安排活动促进学生的深度体验时，数学深度学习过程才真正发生，才能真正意义上培养和发展学生的数学核心素养[3].

参考文献：

[1]郭华.深度学习及其意义[J].课程·教材·教法，2016（11）：25-32.

[2]潘津.基于核心素养的高中数学小组合作学习设计研究[J].高考，2020（8）：29-30.

[3]韩俊元.创新课堂教学，培育核心素养——“一次函数的图像（第一课时）”教学及反思[J].中学数学教学参考，2017（29）：6-8.