遵循认知规律，注重过程体验，提升数学素养

摘要：文章记述了“矩形的性质”一课的教学预设及教学过程.教师在设计教学时，通过让学生类比平行四边形性质的探究路径展开探索，在过程体验中感受数学思想，积累活动经验，提升数学素养.通过教学实践，提出理解学生、理解教材、理解教学可以让教学更具适应性、针对性和有效性.

关键词：认知规律；数学素养；矩形的性质

教学规律是通过大量教学实践探索得出的，是随着教学实践的发展变化而发展的.新课改风向标下，数学课堂发生了翻天覆地的变化，不管是情境的创设还是活动的设计，都指向了对教学规律的研究.教师唯有从理解学生、理解教材、理解教学的角度设计教学，才能提高教学的针对性、有效性和适应性[1].据此，笔者结合“矩形的性质”一课的教学，谈谈如何遵循认知规律优化教学设计，提高学生的数学素养.

1 课前思考

基于生长数学的视角，可以发现“矩形”一课有着明显的生成路径，原因在于学习该内容时学生已然具备了研究平行四边形的探究经验，类比平行四边形的探究路径来探究矩形不仅利于新知的建构，而且对后续菱形、正方形性质的学习可以起到促进作用.进一步分析教材可知，本节课是矩形第一课时，且探究的是矩形概念及相关性质，因此不能仅仅停留在知识的传输层面，还需注重过程体验，引领学生经历图形基本性质的探究过程，以发展基本推理能力.

2 教学过程

教学目标：（1）知识与技能.掌握矩形的基本性质，包括对角线相等、对角线互相平分、内角为直角等；（2）过程与方法.通过类比探究，掌握矩形性质的推导过程，培养有效推理能力；（3）情感态度与价值观.激发对几何的学习兴趣，增强逻辑思维能力.

环节1情境导入，引发兴趣

师：同学们，请你们仔细观察老师手中的书本，它有什么特别的地方吗？

生1：它有四条边，而且它的角都是直角.

师：很好，观察得很仔细.我们可以更精确地描述它的特征，它的几个角是直角呢？

生2：它的四个角都是直角.

师：非常好！那么，今天我们就来研究一下矩形这种常见的几何图形，看看它到底有哪些性质.

环节2类比探究，有所感悟

师：（展示不同的四边形：平行四边形、菱形、矩形、正方形）请同学们观察这些图形，你们发现它们有哪些共同点和不同点？

生1：它们都有四条边.

生2：它们的对边都平行.

生3：正方形和矩形的四个角都是直角，其他图形不是.

…………

师：很好，观察得很仔细.让我们用数学的语言来总结一下矩形和正方形的区别.①边长：矩形对边相等，即相对的两条边长度相等，但四条边的长度不一定相等，正方形四条边长度都相等；②对角线：矩形的对角线相等且互相平分，正方形的对角线相等且互相平分，并且对角线互相垂直；③内角：矩形的四个内角都是直角（90°），正方形的四个内角也是直角（90°）；④特殊性质：矩形没有所有边相等的限制，只要求对边相等和四个直角.正方形既具备矩形的所有性质（对边相等且平行、四个直角），又具备所有边相等和对角线互相垂直的特性.正方形是特殊的矩形，也是特殊的菱形.

环节3有效推理，获取认识

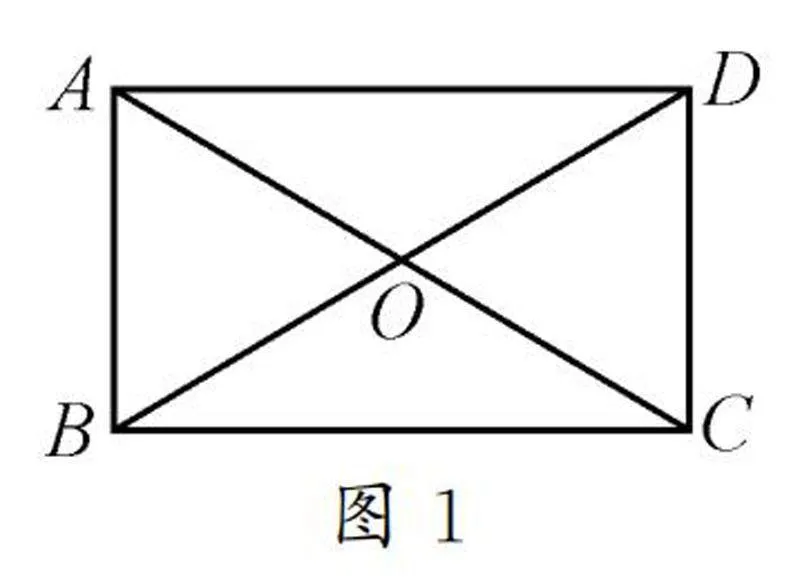
师：请同学们观察图1，除了前面总结的矩形性质，我们还可以得到哪些信息呢？

生1：可以发现OA=OB=OC=OD.

生2：对角线将该矩形分为四个面积相等的等腰三角形.

师：非常好！还有其他发现吗？

生3：发现这个矩形中有四个特殊三角形是四个全等的直角三角形.

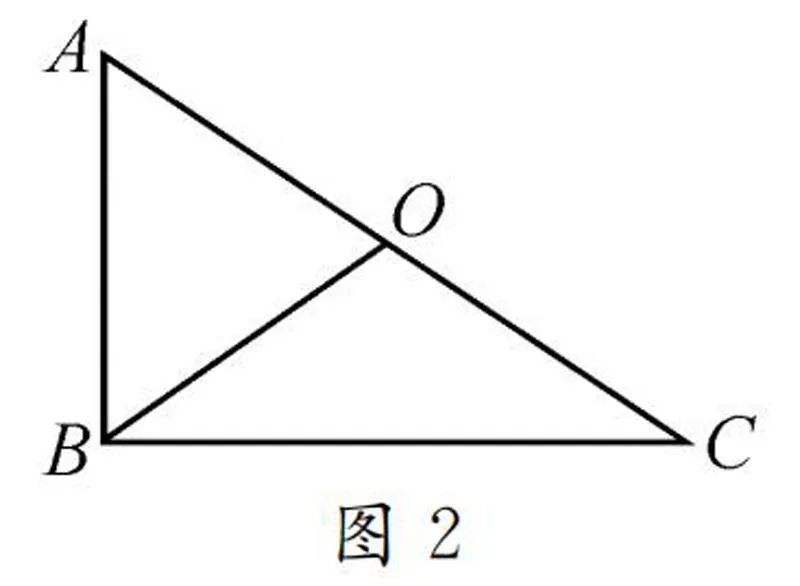
师：很好.观察图2所示的直角三角形，你们有没有什么新发现？

生4：OA=OB=OC，即直角三角形中，斜边中线等于斜边的一半.

师：非常好！你们通过观察和推理，不仅发现了矩形的一些基本性质，还推导出了直角三角形的一个重要性质.这说明你们已经很好地掌握了这些几何知识，并且能够灵活运用.

环节4课堂小结，深化认识

师：请同学们总结一下，矩形有哪些主要的性质？

生（齐）：矩形有四个直角.

师：很好，这是矩形的一个重要性质.还有其他的性质吗？

生1：矩形的对角线相等且互相平分.

师：非常好，总结得很全面.那么，同学们知道矩形在我们生活中有哪些应用吗？

生2：书本的封面和每一页都是矩形.

师（继续引导）：非常正确！书本是一个很好的例子.为什么书本会设计成矩形的形状呢？

生3（尝试回答）：可能是因为矩形有四个直角，便于印刷和装订，而且每一页内容都可以对齐.

师：说得很好.除了这些，矩形的设计还有什么好处呢？

生4（思考后回答）：矩形的书本还容易叠放和携带，这样可以节省空间.

师：完全正确.矩形的设计确实具有实用性和美学价值.它在我们的生活中无处不在，不仅方便了我们的生活，还为我们带来了美的享受.希望同学们能够在学习和生活中多加留意，发现更多关于矩形的应用.

环节5深化认识，拓展应用

师：通过本节课的学习，我们已经了解了矩形的许多性质.那么，老师想给大家一个拓展任务，你们在生活中能发现哪些矩形的应用实例呢？

生1：家里装修时，我发现师傅们都会用矩形瓷砖来铺地，这样可以确保地面平整，容易对齐.

师：这个例子也很好.矩形瓷砖确实利用了矩形的性质，确保地面铺设得美观和稳固.那么，矩形的哪个性质在这里特别重要呢？

生2：我觉得可能是矩形对角线相等和互相平分的性质，这样可以确保每块瓷砖都能对齐.

师：非常棒！这个性质在实际应用中确实非常重要.比如，在制作和检测桌子、书柜等家具时，这个性质就尤为关键.谁能详细解释一下呢？

生3：通过测量对角线长度来确保每个角度都是90°，从而保证家具的平整和稳定.

师：很好.如果对角线长度相等且中点重合，就能确认家具的形状是标准的矩形，这样制作出来的家具不仅美观，还能保证其稳固性和功能性.通过这节课的学习，希望大家不仅掌握了矩形的性质，还能在生活中应用这些知识.

3 教学反思

3.1 理解学生，让教学更具适应性

培养学生的数学核心素养，提升学生分析和解决问题的能力，单纯地依靠解题是难以实现的，而需让学生参与数学探究，经历知识生成过程，才能积累一定的活动经验[2].为此，本节课中教师能遵循学生认知规律，通过问题引领探究，帮助学生初步感受矩形性质的特殊之处在于“对平行四边形的一个内角条件的强化”，体验研究路径的类似，从而轻车熟路地展开对矩形性质的探究.就这样，经历知识生成的过程，在类比和对比的过程中深化认识，实现对数学知识和方法的深刻理解，有效发展数学素养.

3.2 理解教材，让教学更具针对性

四边形概念、要素、性质等的教学是类比三角形展开的，通过回顾三角形的探究过程，逐步形成了几何图形研究的一般性思路，实现了知识和方法的共同生长，同时明确了几何图形的研究路径，即“定义—性质—判定—应用”，如需深入，则是探讨图形的特例.因此，在设计本节课的教学活动时，笔者充分尊重教材，并挖掘教材内涵进行提问，让所有问题围绕类比和对比展开，让学生体会几何图形的一般研究范式，从而有效渗透类比思想，促进知识体系的建构.

3.3 理解教学，让教学更具有效性

提高基于具体学情和教学内容的探究活动的有效性，教学的着力点不仅在于知识的获取，更在于学习过程中的体验和感悟、数学思想的体验及活动经验的积累[3].本课中，教师注重引导学生观察平行四边形动态变化的过程，让学生切实体验变化的性质、不变的性质及变化的规律，从而在变与不变中丰富学生的世界观.教是为了不教，在课堂中注重引导学生经历和体验，让学生自主发现和建构，不仅有助于知识网络的构建，还有利于后续菱形等的学习，更重要的是帮助学生掌握研究的方法和思路.

总之，培养学生的数学素养并非一蹴而就的，需要渗透在每一节课中，并一以贯之地把握课堂教学中各个环节的设计，做到遵循学生认知规律，关注学生已有知识水平、数学思维和已有经验，真正意义上注重过程体验，才能提高学生探究的参与度，让学生真正进入深度学习，有效提高数学核心素养.

参考文献：

[1]徐淮源.基于教材理解下的高中数学概念教学设计——以“三角函数的周期性”为例[J].教育研究与评论（中学教育教学），2010（2）：73-78.

[2]陈明钟.实施过程性教学模式 构建初中数学高效课堂[J].中学数学，2016（8）：68-70.

[3]夏炳文.强化“三个理解” 打造活力课堂——以一节试卷讲评课为例[J].中国数学教育，2016（10）：42-44，56.