初中数学“以自主学习为中心”课堂教学的探究

摘要：高效优质的初中数学课堂教学是指向学生发展的教学，是学生在数学学习过程中主动探究的教学.本文中以“三角形全等的判定（SSS）”为例，着眼于学生的“学”，以问题导向的自主学习为中心，通过布置预习任务、设计问题串、展开小组合作探究、优化练习设计，引导学生自主合作进行探究学习，使学生主动参与到数学学习中，创新课堂教学模式，实现高质量数学课堂教学，改变以往课堂教学指向知识落实的情况，转变为促进学生思维力、学习力的全面提升.

关键词：初中数学；自主学习；优质教学；课堂探究

高效优质的数学教学不是以教师讲得精彩为标准，而是要看学生在学习过程中能否主动融入自己的思考，根据已有知识对新知识进行建构［1］.换言之，要判断数学教学是否高效，关键看学生的“学”.“自主学习”以“以学为本”为基本原则，以自主、合作、探究为基本途径，以问题导向为核心要素，以创造学习、对话学习、选择学习为主要方式，是一种促进学生思维力、学习力全面提升的课堂教学方式［2］.采用这种方式教学时，需要教师在课前布置自学任务，学生自主解决能够自己解决的问题，在课堂上通过合作学习及教师引导提高学习力，提升学习效果，培养核心素养.

1 布置任务，提前预习

1.1 “自主预习”教学策略

“凡事预则立”，预习的目的是让学生提前自主感知新知识，在阅读教材中获得对新知识的初步认知，为课堂探究活动打下基础.在预习过程中以任务的形式引导学生预习，以明确的任务让学生了解什么、知道什么、该做什么，要真正做到心中有数.“三角形全等的判定（SSS）”教学中的预习任务如下：

（1）阅读教材（人教版）第35-37页，结合“图12.2-1”思考教材中的问题；

（2）结合“探究1”和“探究2”，知道三角形全等的“边边边”判定定理；

（3）自主阅读“例1”，尝试写出证明过程；

（4）自主尝试完成练习第1题.

第（1）个任务是让学生在阅读教材中，结合之前所学，思考如何判定两个三角形全等；第（2）个任务是让学生结合探究活动，初步了解三角形全等的“边边边”判定定理；阅读例1则是让学生根据判定定理学习证明过程；练习则是引导学生尝试应用.

1.2 设计问题串

为更好地帮助学生完成预习任务，在课堂中采用提问的方式对学生的预习情况进行检查.问题如下：

（1）只给一个条件（一条边或一个角）画三角形时，所画三角形一定全等吗？

（2）给两个条件画三角形时，有几种情况？每种情况下画出的三角形一定全等吗？

具体设问为：①三角形的一个内角与一条边.②三角形的两个内角.③三角形的两条边.

（3）如果给出三个条件画三角形，你能说出有哪几种可能的情况？

先引导学生探讨问题，增强学生的自主性，教师适时对学生的预习进行评价，激励学生.

2 合作探究，生生互动

预习的目的是让学生学会自主学习.学生在预习中遇到的问题，进入课堂后，以小组形式展开探究，学生互帮互学.一是通过互帮互学增强学生间的信息交流，培养学生的思考和语言交流能力，促进学生理解和巩固新知识.二是要利用合作的方式，让学生共同解决问题，并在合作中构建新知.尤其是要注重引导学生展开交流活动，以问题启发学生观察、思考，在活动中获得对数学知识的理解.结合三角形全等的判定（SSS）的重点和难点，本次教学中的探究活动如下.

2.1 质疑引思

利用课件展示教材中的“图12.2-1”，我们知道，如果△ABC≌△A′B′C′，那么它们的对应边和对应角都相等.要证明两个三角形全等，是不是要满足三条边和三个角分别对应相等？如果不是，可以选择哪些条件来判定两个三角形全等？

2.2 画图求证

（1）任意画出一个△ABC.（学生自主操作.）

（2）满足六个条件中的一个或两个，再画出一个三角形△A′B′C′，两个三角形是否全等？（学生画出图形后进行交流.）

（3）任意画出一个△ABC，再画出另外一个三角形A′B′C′，使AB=A′B′，BC=B′C′，CA=C′A′，将△A′B′C′剪下，看其是否能与△ABC完全重合？（作图时，根据教材第36页引导学生作图，个别指导.学生按要求作图后剪下观察.）

2.3 交流与展示

（1）你发现了什么？（学生在小组交流的基础上到讲台上展示.）

（2）结论：三条边分别相等的两个三角形全等.（结合学生的表达，教师板书或呈现课件.）

（3）结合图形表达：因为AB=A′B′，BC=B′C′，CA=C′A′，所以△ABC≌△A′B′C′.（教师先出示图形，展示的学生用数学语言在黑板上边讲边书写，最后教师点评并规范书写.）

2.4 标杆题探究

课本例1：在三角形ABC钢架中，AB=AC，AD是连接点A与BC中点D的支架，求证△ABD≌△ACD.

阅读例1，交流已知条件是什么？（关键抓住“AD是连接点A与BC中点D的支架”）题干中只给出了AB=AC这一条件，要求证△ABD≌△ACD，还需要哪些条件？

小组合作交流：欲证△ABD≌△ACD，只需判定这两个三角形三条边分别相等即可，题干中已知AB=AC，又AD是两个三角形的“公共边”，那么只要再求证BD=DC即可.而题干中告诉我们“AD是连接点A与BC中点D的支架”，所以BD=DC，由此可知两个三角形三条边分别相等.

引导学生写出证明过程，并抽小组上讲台展示：

∵D是BC的中点，

∴BD=DC.

在△ABD和△ACD中，

AB=AC，

BD=CD，

AD=AD.

∴△ABD≌△ACD（SSS）.

2.5 技能培养

由三边分别相等判定三角形全等的结论，还可以得到利用直尺和圆规作一个角等于已知角的方法.（该环节中，学生相互交流完成作图，教师利用课件或板书演示.）

新课标中指出，数学教学是让学生经历数学知识的形成过程.以讲授的方式将知识告诉学生，学生只是被动的记忆，很容易遗忘，难以理解掌握；让学生在探究中学习，更多的是让学生自主探索发现问题，互帮互学，加深对知识的理解，巩固知识，形成知识体系.在本次教学中，以问题激发学生的探究兴趣，利用画图求证的方式引发讨论，得到结论后再过渡到标杆题，学习论证的表达.

3 课堂检查与延伸

在数学教学中常出现“为了练而练”的现象，且练习的形式较为单一，更多的就是让学生用作业本抄写书本上的练习，完成后交由教师批阅.练习是一种检查的方式，目的是检查学生对所学数学知识的掌握情况，引导学生运用课堂中所学的知识解决问题.在练习中，不仅要考虑学生的实际情况，且要注重合作.结合本次课堂教学，设计练习如下：

3.1 课堂检查

完成课后练习（教材第37页）第1题和第2题.

对于第1题，先小组交流，写出论证过程并相互对照检查.

对于第2题，自主观察，找出OM=ON，OC是公共边，交流CM=CN，再求证.

3.2 拓展延伸

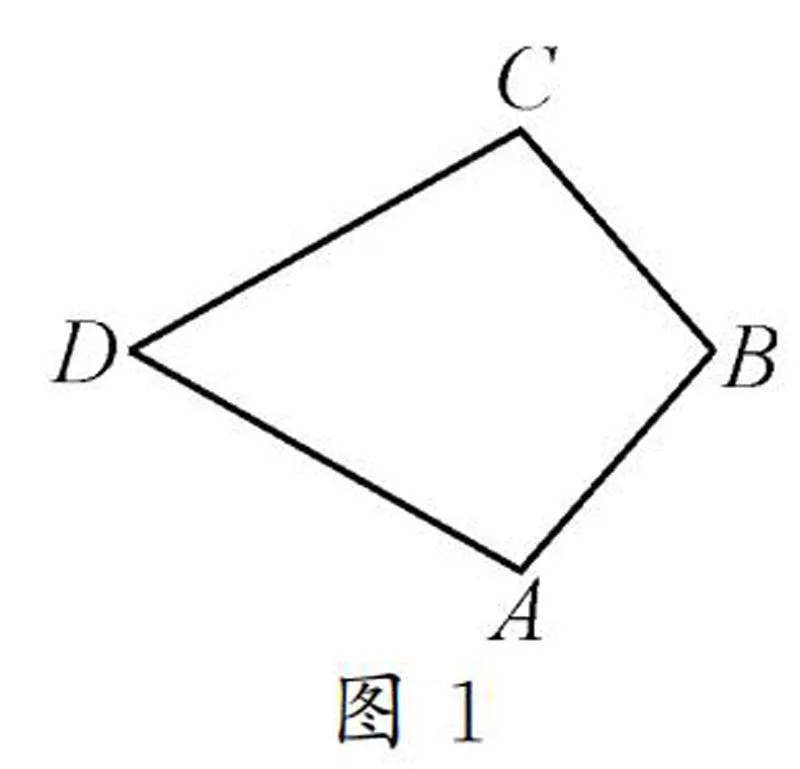
如图1，已知四边形ABCD中，AB=CB，AD=CD.

求证：∠C=∠A.

该题要求学生进行图形构造，连接BD构造△BCD和△BAD，利用“边边边”判定定理证明△ABD≌△CBD后，求证∠C=∠A.

4 总结

从本次课堂教学实践情况来看，学生对三角形的判定定理（SSS）的掌握情况优秀，达到了预期的教学目的.高效优质的数学教学并不是以教师讲得精彩为标准的，更多的是要看学生在学习过程中的表现及对知识的掌握情况.换言之，要判断数学教学是否高效优质，关键是看学生的“学”.为让学生能更好地融入到数学学习过程中，需从以下几方面加强教学设计：首先，要结合学生的认知情况和教学目标，精心设计预习任务.在设计预习任务时，要明确让学生做什么，怎么做，以及达到什么目的.其次，要精心设计探究活动，明确探究活动的目的、问题设计、学生应该做什么及教师应该做什么等.最后，优化练习设计，通过练习达到巩固的目的.

总之，在初中数学教学中，着眼于学生的“学”，充分体现学生的自主性，结合学生实际设计好预习任务，组织学生展开小组合作探究，优化练习设计，促使学生主动参与数学学习，点燃学生的探究欲望，同时提高学生创新思维能力.这样的教育是以素养为核心的教育，让数学教学变得更加高效优质.

参考文献：

[1] 陈梅珍.建构“学为中心”的初中数学课堂[J].中学数学，2019（18）：73-74.

[2] 秦莉.基于初中数学文本阅读促进自主学习的策略[J].中国教师，2018（6）：76-79.