回归教材重探究，问题寻“多”显素养

摘要：在初中数学解题教学过程中，我们往往忽视了教材中“典型问题”的探究，靠题海战术进行强化训练.本文中则针对教材中的典例，进行回归探究，在探究一题多解、一题多变、一题多思的过程中，探索数学知识点的巧妙运用，体验数学方法与思想的指导与融合，从而更好地提高学生解题能力，提升学生数学核心素养，真正落实“双减”.

关键词：初中数学；回归教材；一题多解；一题多思；核心素养

《义务教育数学课程标准（2022年版）》中已经明确指出：确立核心素养为导向，以学生发展为本，进一步强调学生获得数学“四基”，运用数学知识与方法发展“四能”，形成正确的情感、态度和价值观，考查的问题必须以教材为基准点，立足教材，根据学生能力发展适度拓展，以信度、效度和区分度为基础，以教师有效教学指导为导向，让教材问题成为评价学生核心素养达成的重要载体.

1 教材原型试题呈现

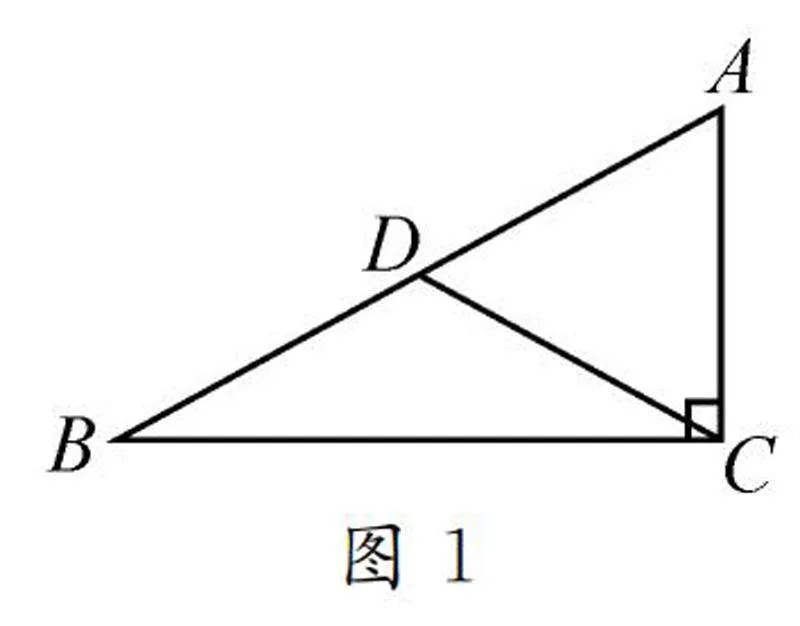
课本原型问题如图1，画Rt△ABC，并画出斜边AB上的中线CD，然后量一量，比较一下看看CD与AB的长度关系是怎么样的.

通过测量，相信你会发现：CD恰好是AB的一半.下面让我们用演绎推理证明这一猜想.

已知：在Rt△ABC中，CD是斜边AB上的中线.

求证：CD＝1／2AB.

2 回归教材探究本质

多解多题归一是培养学生数学思维聚合性的好方法、好思路，这就需要我们教师在教学过程中要抓住任何机会让学生体现创造过程，从而感受发散思维和聚合思维完美融合的成功感与成就感.多解多题归一就是针对这方面的专题训练，虽然遇到的问题不会完全相同，但是却能从“异”中探“同”，从“同”中寻“异”.面对我们所遇到的“型异质同”或“型近质同”等问题的探究分析，可从中提炼问题的本质特征，从而探寻问题存在的内在规律，做到解题举一反三、触类旁通、事半功倍.这既能体现“数学核心素养”培养目的，更能深入落实“双减”政策，真正摆脱“题海”的累赘，做到轻松学习.

3 一题寻“多”提素养

3.1 一题多解提升素养

针对课本原型问题我们可以思考得到如下解法：

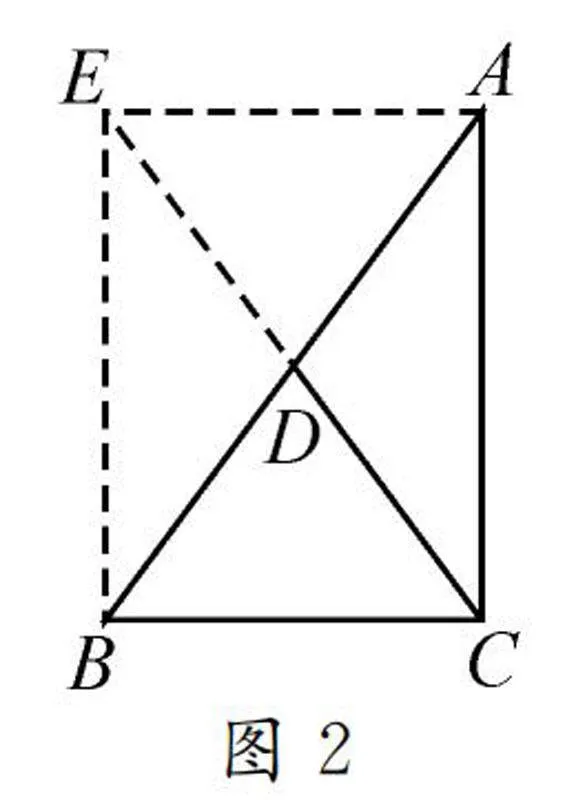
解法一：构造法.

如图2，延长CD到点E，使DE＝CD，连接AE，BE，这样可以得到CD＝1／2CE.又CD是直角三角形斜边AB上的中线，从而可得AD＝BD，因此可以得到四边形ACBE是平行四边形.再结合∠ACB＝90°，判断得到平行四边形ACBE是矩形.故CE＝AB，即CD＝1／2AB.

解法二：相似法.

如图3，过点D作AC的垂线，垂足为E.因为∠ACB=90°，所以DE∥BC，则△ADE∽△ABC.因为D是AB的中点，所以AD∶AB=1／2，从而得到AE∶AC=1／2，即DE是AC的垂直平分线，则有AD=DC.故CD＝1／2AB.

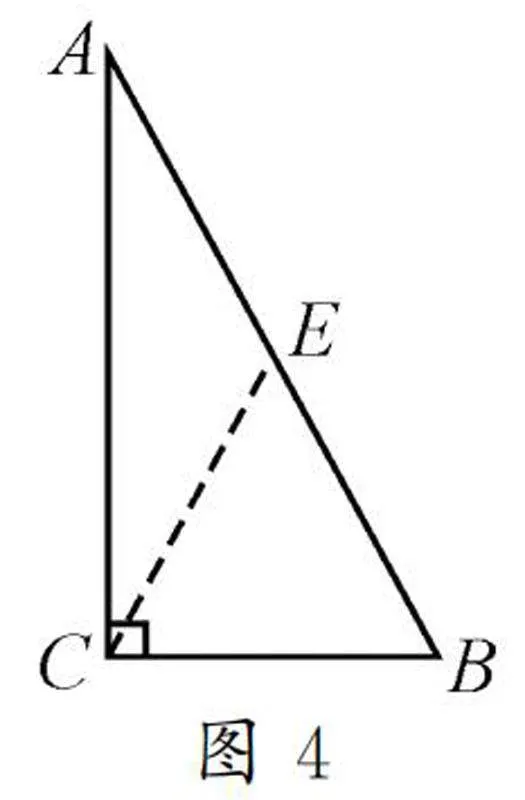
解法三：作角法.

如图4，在∠ACB的内部作∠BCE＝∠B，CD与AB交于点E，则BE=CE.

又根据∠BCE+∠ACE＝90°，∠B+∠A＝90°，可得∠ACE＝∠A，则EA＝EC.故EA＝EB＝EC，即CE与CD重合，且CD=CE＝1／2AB.

从上面的解法中我们可以发现，不同的方法着眼点不同，解题思路不同，所体现的数学基本知识也存在着差异.多种方法的体现也真正考查了学生对基本知识的掌握能力和运用数学知识的能力，从而起到提升数学核心素养的作用.

3.2 一题多变促进发展

例如，张老师指导学校数学兴趣小组进行如下问题探究：

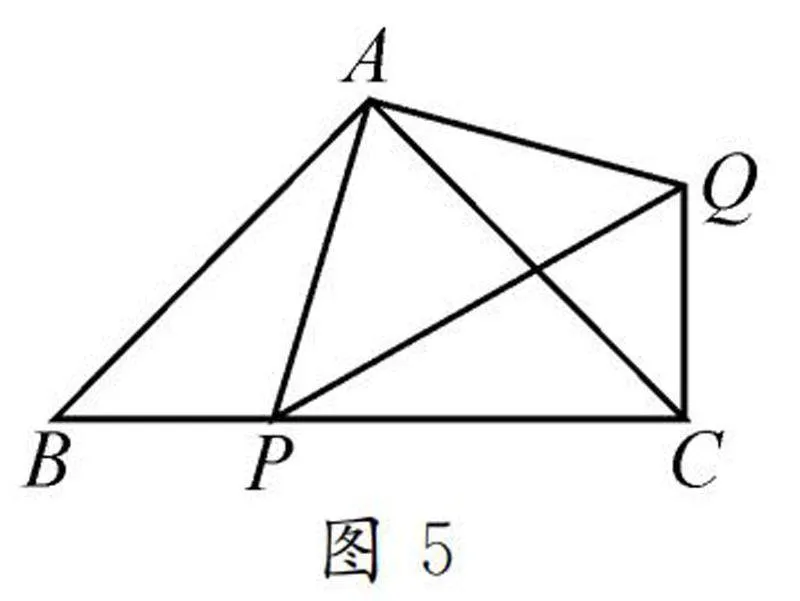
原型问题如图5，在等腰直角三角形ABC中，∠BAC＝90°，P是斜边BC上一点，连接AP，以AP为腰作等腰直角三角形APQ，且∠PAQ＝90°，连接CQ，判断BP和CQ的数量关系.

解题思路：根据题意可以由∠BAC=90°=∠PAQ，得到∠BAP＝∠CAQ，从而得到△ABP≌△ACQ，即可得出结论.

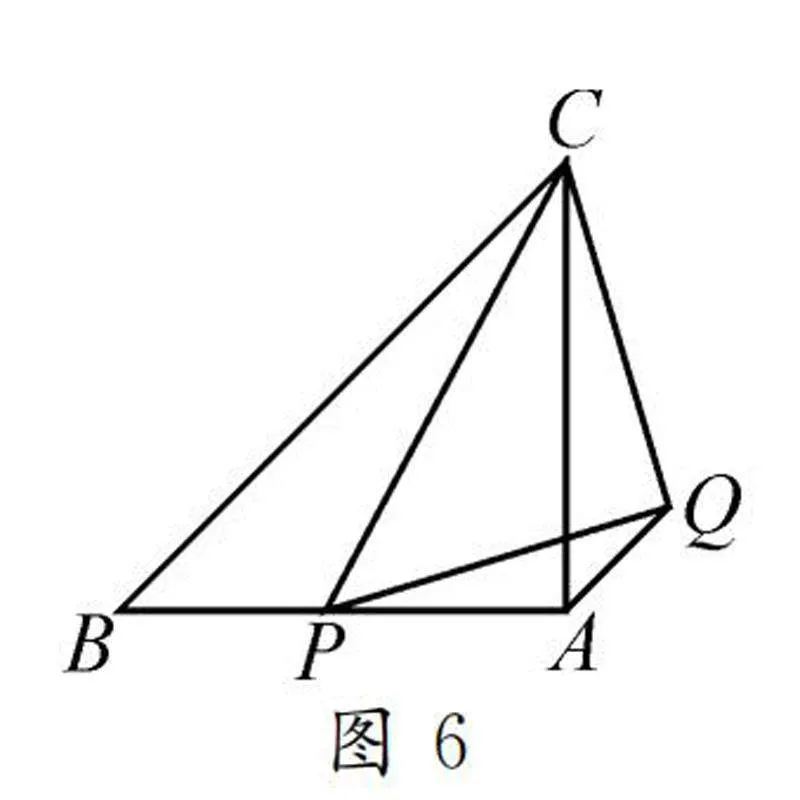
变式1如图6，将原型问题中点P的位置由斜边变化至某条直角边上，连接CP，再以CP为底边作等腰直角三角形CPQ，连接AQ，判断BP和AQ的数量关系.

解题思路：由题意得∠PCQ＝45°=∠BCA，则可判断出∠BCP＝∠ACQ，再判断出BC／AC＝CP／CQ＝2，得到△BCP∽△ACQ，即可得出结论.

变式2如图7，如果将原型问题中的等腰直角三角形转化为正方形ABCD，在边BC上有一点P，再以DP为边作正方形DPEF，其中心为点Q，连接CQ，判断DP，CQ和CD之间的关系.

解题思路：根据图形的特点，易得出BP＝2CQ，从而再根据两个正方形边长与其关系利用勾股定理建立方程求解，即可得到答案.

综合上述变式可知，针对同一个问题，我们可以在位置和图形形状上进行变化，解答过程中涉及的知识点也随之变化，一题多变让学生在解答过程中充分得到思维的发散，问题的求解让知识点充分展示出来，数学核心素养从而得到提高.

3.3 一题多思深挖思想

问题展示如图8，在等腰三角形ABC中，AB=AC，延长CA至点E，延长AB至点D，使得BC=CE=DE=AD，试求∠BAC的度数.

解题思路：由题意发现，相等的四条边形成一个凹形四边形，根据我们所学知识点，很难将这些条件进行巧妙运用.这就需要进行变化，故可思考将BC平移至DF处，如图9，连接CF，自然构成了平行四边形，再根据平行四边的性质可得BD＝CF，DA∥FC，则∠EAD=∠ECF，利用“SAS”判定△ADE≌△CEF，所以ED＝EF，从而可推出△DEF为等边三角形.设∠BAC＝x，则∠ADF＝∠ABC＝180°－x／2，根据三角形内角和定理可分别表示出∠ADE，∠ADF，根据等边三角形的性质不难求得∠BAC的度数.

从上面的问题我们可以思考得到：其一，利用平移变换将相等的边转移在同一个三角形内，构造特殊三角形，便于利用相关条件进行解答；其二，针对相等的边所对应的三角形构造全等形，利用全等三角形的性质进行边、角的转化，形成问题突破点；其三，整个问题条件中没有涉及到角度，但求的是角度，这就需要我们利用角度之间的关系，建立方程，进行解答，特别是出现角度之间的倍数关系时也要注意利用方程思想来突破.

综上所述，不管是一题多解、一题多变，还是一题多思，都是在教学中注意指导学生不断领会数学问题中所体现的思想，训练思维品质，更是借助“多”的思考培养学生的发散性思维，激发学生学习兴趣，培养思维的灵活性，从而更好地促进学生数学核心素养的提升.

4 多解归一激活思维

多题归一的训练，达到使学生巩固与深化所学知识，提高解题技巧及分析问题、解决问题的能力，增强思维的灵活性的目的.通过训练，学生达到对知识认识的全面性.同时，还要重视解题反思，形成系统化认识.通过反思，引导学生回顾概括数学结论的整个思维过程，检查得失，从而加深对数学原理、通性通法的认识;通过系统化，建立新知识与已有认知结构中相关知识的横向联系，井概括出带有普遍性的规律，从而推动同化、顺应的深入.这样的教学方法有利于培养学生思维的灵活性，增强应变能力.

问题探究是解决数学的关键，方法指导是数学突破的手段，思想利用是解决问题的灵魂所在.我们借助教材中的典型例题进行“多元”突破，让数学问题、数学知识、数学方法、数学思想进行巧妙融合，形成相互影响、相互联系和统一发展的辩证统一体，让问题解答过程中所体现的内在关系得到充分的展示，灵活体现问题的“多元化”，让学生能力得到提高、数学核心素养得到提升.