“变”的教育价值

摘要：数学教学重在培养学生的思维，创造性思维的培养是教师创新教法的源动力所在.因此，教师的教学不能一成不变，而应处于不断改革创新中，是为“变”.“变”，教与学中无处不在.尤其是在核心素养理念深刻影响数学课堂教学的当下，“变”正发挥着重要的教育价值.那么，何为“变”？为何“变”？如何“变”？将成为今后一段时间内教师教学中常思考的几个问题.

关键词：“变”；教育价值；正方形；变式

要研究“变”的教育价值，首先要清楚何为“变”？粗略来讲，“变”就是变化.在教育层面，“变”就是教育理念的变化；在教学层面，“变”就是教学方法的变化，即教法的改革与创新；在课堂实践层面，“变”就是利用变式教学拓展学生的思维，让学生的解题能力得到提升.其次，要清楚为何“变”？传统的教学固化了学生的思维，不利于学生的全面发展.素质教育背景下的数学教学要求教师打破传统，勇于创新，因为“变”的教育价值体现在有利于培养学生科学思维能力、有利于提高学生的解决问题能力、有利于增强学生的自主探究能力等方面[1].最后，如何“变”？这才是“变”从理论到实践的关键.

1 课前三思

北师大版九年级上册第一章的最后一节安排了正方形的两个课时内容，分别介绍了正方形的性质和判定.在介绍正方形的性质时，先通过“议一议”引导学生初步感知正方形与菱形、矩形的区别，从而获得正方形的两个性质定理（正方形的四个角都是直角，四条边相等；正方形的对角线相等且互相垂直平分）.然后通过“想一想”激发学生的思维，并引导学生思考正方形的对称性（轴对称性：正方形是轴对称图形，有四条对称轴；中心对称性：正方形是中心对称图形，对称中心是对角线的交点）.不难发现，这些都是进行正方形旋转变式教学的基础.接下来，进行例1的讲解与分析：

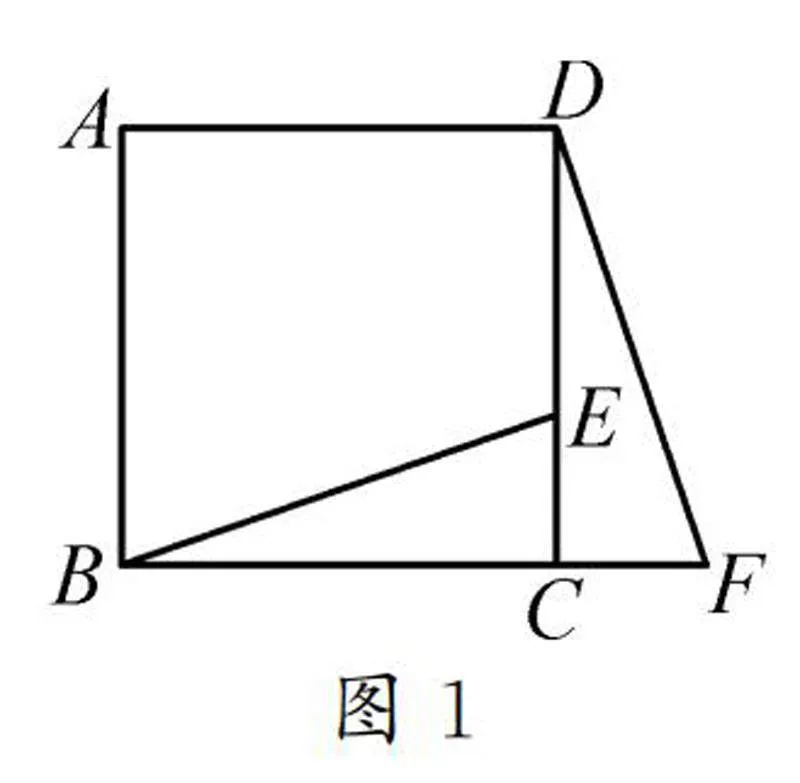
例1如图1，在正方形ABCD中，E为CD边上的一点，F为BC延长线上一点，且CE=CF.BE与DF之间有怎样的关系？请说明理由.

看到该例题，笔者联想到与其融合的旋转问题.考虑到旋转是解决该类问题的重要方法，同时当前很多学生对旋转的应用不够灵活，因此笔者对本节课的内容进行拓展.于是进行了如下思考：

思考1除了借助例1传授基础知识和基本技能外，还可让学生学到什么？

正如上述，本节课须在讲解例1的基础上进行拓展.观察图1不难发现，本题不仅可以用全等三角形解决，还可从旋转这一角度入手.因此，本例题还可以让学生进一步了解旋转在正方形中的应用.

思考2如何引导与衔接？

用旋转解决问题，其思路主要是借助转化思想.因此，在拓展时会面临两个问题：首先，如何引导学生进行变式？即“如何变？”其次，如何让学生的思路在转化前后实现有效衔接？笔者认为，这其实是“变法”与“解法”的问题，可分别从旋转中心和旋转图形、旋转的性质入手（见教学过程）.

思考3如何提炼并应用？

变式拓展教学的目的，不仅是为了激发学生的思维，也是为了让学生提炼出“变”的方法及“变”后的解法.基于这一思考，笔者与学生在小结环节开展积极合作.

2 教学过程

2.1 常规解析

本例题主要是借助正方形的性质判断两条线段间的关系，这种关系包括数量关系和位置关系，即BE=DF，且BE⊥DF.

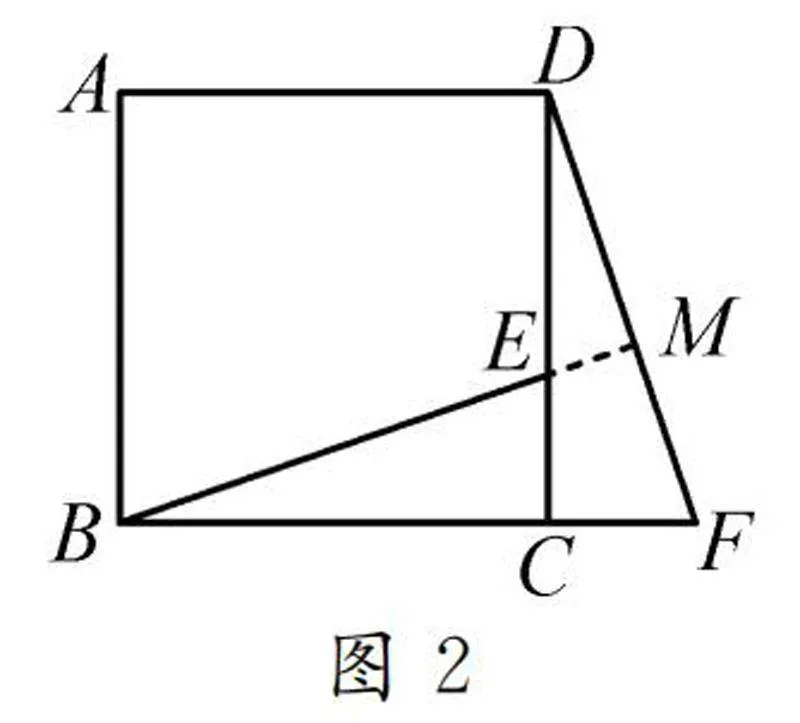
解析：因为四边形ABCD是正方形，所以BC=DC，∠BCE是直角，且易得∠DCF也是直角，故∠BCE=∠DCF.结合CE=CF，易证得△BCE≌△DCF，最终证得BE=DF.对于位置关系的判断，先延长BE交DF于点M（如图2）.因为△BCE≌△DCF，所以∠CBE=∠CDF.由∠DCF是直角，可知∠CDF+∠F=90°，所以∠CBE+∠F=90°，进而证得∠BMF=90°，故BE⊥DF.

2.2 激思变式

2.2.1 一问

师：刚才我们通过三角形全等证明了BE=DF，又通过角与角之间的关系证明了BE⊥DF.那么，有没有其他的方法解决本题呢？

（学生经过思考、讨论，发现△DCF可以看成是△BCE绕着点C顺时针旋转90°形成的.）

生：老师，我发现△DCF和△BCE两个三角形像是一种旋转变化.

师：非常好！那么我们能根据旋转解决本题吗？

（学生发现思维“生长点”，并积极主动探索.）

评析：突破常规思维，引导学生仔细观察，并鼓励学生用自己的方式进行猜想，这正是变式拓展教学的前奏.只有学生突破了常规思维，才会产生不同的审题视角.这对促进学生发散性思维的形成与发展有利，同时也是后续变式拓展的基础.

经过思考和探究，学生利用旋转解决本题的思路大致如下：

首先，由BC=DC，CE=CF和∠BCE=∠DCF结合旋转判断出，△DCF可以看成是△BCE绕着点C顺时针旋转90°形成的.继而，根据图形旋转的性质“对应边相等”证得BE=DF.最后，同样根据图形旋转的性质得到BE与DF在旋转过程中形成的角等于旋转角，即BE⊥DF.

2.2.2 二问

师：既然△DCF是△BCE围绕着正方形的顶点C旋转而形成的，那么在正方形中还可以怎样旋转？

（该问一出，犹如一石激起千层浪，学生马上投入到激烈的讨论中.）

教师选学生代表谈一谈思路.

生1：我觉得是不是可以让三角形旋转后再翻折，得到△DCF关于DC的对称三角形.

生2：我认为可以将△BCE换成一个正方形，让该正方形绕着点C旋转.

生3：我还觉得可以让这样的正方形绕着正方形ABCD的中心旋转.

…………

师：大家的思路都很不错，能不能根据自己的想法画出图形并给出一定的条件呢？

生：可以（画图）.

经过一番操作，学生获得了下面三个变式：

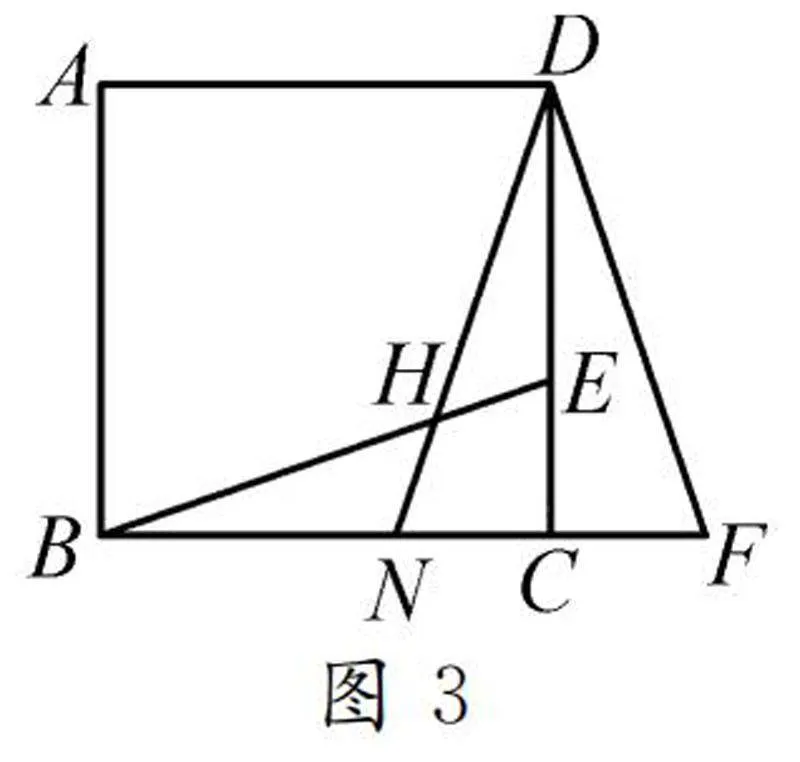
变式1如图3，E是正方形ABCD边DC上的一点，延长BC至点F，使CF=CE，连接DF.以DC为对称轴作出△DCF的轴对称图形△DCN，DN与BE交于点H.你能找出全等三角形吗？选择其中一组给出证明.

变式2如图4，正方形ABCD的边长为4.分别取BC，DC的中点E，N作正方形EFNC，并将其绕着点C按顺时针方向旋转45°得到正方形GMHC，FN交GM于点O，求ON的长.

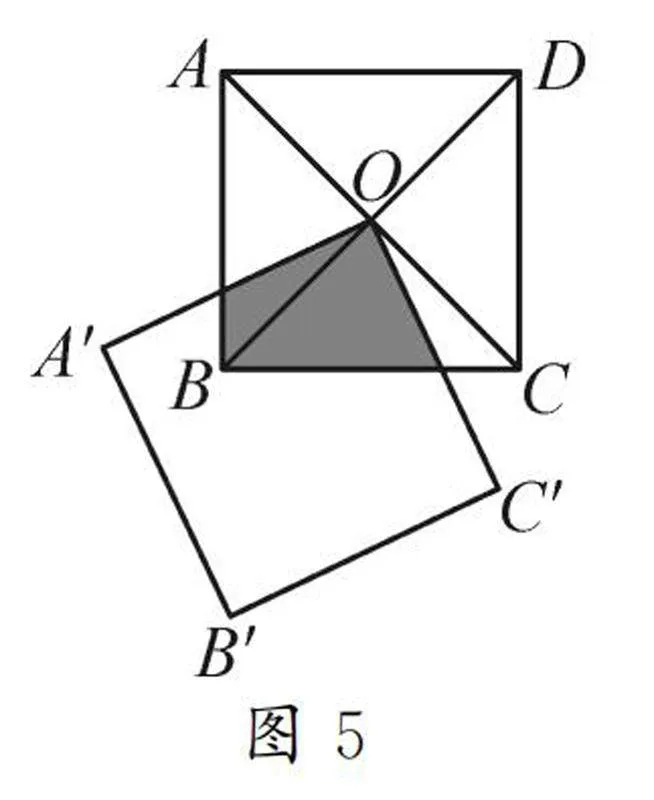
变式3如图5，正方形ABCD的对角线相交于点O，正方形A′B′-C′O与正方形ABCD的边长相等.当正方形A′B′C′O绕着点O旋转，两个正方形重叠部分的面积是否会变化？如果不变，请计算出重叠部分面积与正方形ABCD面积之间的关系;如果有变化，请说明理由.

3 解题小结

在获得变式以后，学生分组完成上述三个变式.这样一来，不仅让学生经历了变式产生的过程，而且通过解决自己设计的变式题，自信心得到提高.

“变”是创造性思维的源泉，让学生“变”，既是解题习惯的“变”，也是解题思维的“变”[2].学生一改以往就题解题的学习方法，深入思考和探究获得变式，不局限于一道题，不断拓展.

总之，教师的教学不能一成不变，要在课堂活动中灵敏捕捉思维的“生长点”，并且激发学生自主探究，让学生参与到变式教学中，不断提高他们的思维能力和解决问题能力.

参考文献：

[1]侯德森.变式教学贵在变之有道——以一道习题教学为例[J].中小学数学：初中版，2018（6）：1-3.

[2]张锋.小题大做的教育价值——以一节正方形复习课的教学为例[J].中国数学教育，2020（19）：10-14.