感悟数学之

摘要：众所周知，培养学生数学学习兴趣是学好数学的关键.在初中数学教学中，教师要摒弃单一的知识讲授，有意识地展示、传播数学之美，并带领学生一起探索、发现数学之美，从而让学生充分体验数学学习的乐趣，激发学生潜能，获得成功的喜悦和美的享受，进而让学生爱上数学.

关键词：兴趣；数学之美；乐趣

通过数学学习，不仅要让学生掌握数学知识，提高数学成绩，还要培养学生数学学习的兴趣，提高学生学习数学的积极性和主动性.在日常教学中，教师应有意识地传播数学之美，并创造机会让学生体验数学之美，从而激发学生对数学的学习兴趣.而数学之美散落于教材的各个角落，教师要去挖掘，并创造机会让学生去欣赏、体验和感悟，以此充分展示数学的魅力.

勾股定理将数与形完美地融合在一起，其中蕴含着丰富的美学资源.教学中，教师应引导学生多视角思考与观察，主动探寻蕴含其中的美妙的数量关系，充分感受美、发现美、验证美，构建高效生本课堂.

1 深入挖掘，凸显本质

在初中数学教学中，若想让学生真正地理解知识，仅将知识讲授给学生并不够，还要关注学生对数学本质的认识，重视引导学生运用所学知识分析问题和解决问题，让学生在学习数学的过程中找到乐趣，提高学生的数学素养和创新能力.在解题过程中，教师要引导学生多思考几个“为什么”，在刨根问底中弄清实质，提高学生的数学能力，让学生感受数学之美.

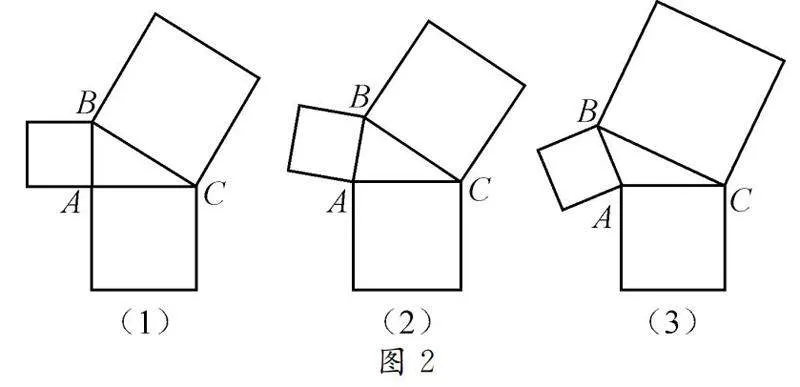
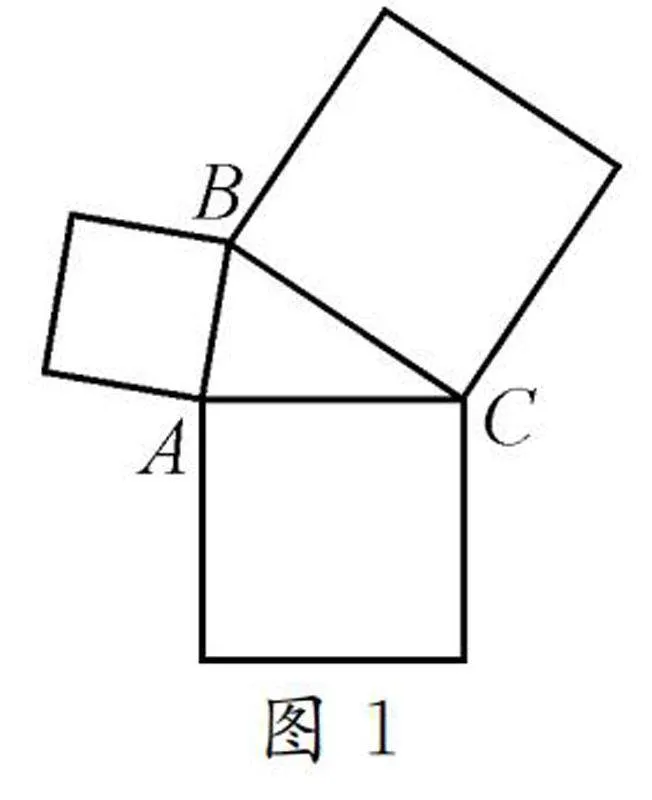
例如图1，已知△ABC是锐角三角形，分别以AB，BC，AC为一边作图1所示的正方形，假设BC边最长，则以BC边为边长的大正方形与另外两个正方形存在怎样的数量关系？如果△ABC是钝角三角形，其中BC边最长，你又能得到怎样的数量关系？

师生活动：问题给出后，教师让学生独立思考，探寻蕴含其中的一般规律.从学生反馈来看，很多学生结合已有知识和经验，利用割补法计算正方形的面积，发现蕴含其中的美妙的数量关系.在此基础上，教师继续追问“是什么原因导致这种现象呢？”在问题的驱动下，学生继续思考，逐渐逼近问题的本质.

探究过程如下：

如图2（1），结合已有知识经验可知，当∠BAC=90°时，AB²+AC²=BC²；如图2（2），保持AC与AB的长度不变，并保证BC边依然为最长边的前提下，调整∠BAC的大小，使得∠BAC<90°，显然此时BC变短了，显然大正方形的面积变小了，而两个小正面形的面积和保持不变，所以AB²+AC²>BC²；同理，如图2（3），在确保BC边为最长边，AC与AB的长度不变的前提下，继续调整∠BAC的大小，使得∠BAC>90°，显然BC变长了，所以大正方形的面积变大了，而两个小正面形的面积和保持不变，所以AB²+AC²<BC².这样以直角三角形为基础，通过调整两个小正方形的夹角大小，引领学生体会面积之间的数量关系，揭示“角变化引起边变化”的实质.

设计意图：在研究勾股定理时，运用“勾股树”证明勾股定理，即以直角三角形的各边为边长向外作正方形，通过割补得到两个小正方形的面积之和等于大正方形面积，从而得到勾股定理.该题将直角三角形转化为锐角三角形和钝角三角形，通过由特殊到一般的转化，点燃学生的探究欲.同时通过由一般到特殊的探究，有利于加深学生对相关知识、方法的理解，摒弃单一的模仿和套用，让学生通过探究感悟数学知识之间的区别与联系，培养思维的深刻性.另外，为了探究产生这一现象的本质原因，教师进行适度引导，让学生在变与不变中认清问题的本质，以此提高学生发现、分析和解决问题的能力，彰显数学探究之美，提高学生数学思维品质.

2 借助问题，引领发现

在传统数学教学中，师生所关注的往往是解题方法和解题技巧，学生眼中的数学往往是枯燥的、乏味的，不利于学生学习兴趣的培养.基于此，在实际教学中，教师要预留时间让学生去探索、去交流，引导学生发现数学之美.

例如，通过对例1的多层次探究，学生得到并验证了一般结论.在此基础上，教师启发学生继续思考这样几个问题：

（1）若其中直角变大和变小的度数一样，那么是不是减少的面积恰好为变大的面积呢？

（2）假如图2（2）和图2（3）中减少和增加的度数一样，先将其合并为图3（1），与图3（2）相比较，是不是图3（1）中正方形FHKJ与正方形BCDE的面积之和等于图3（2）中正方形FHKJ与正面形BCDE的面积之和呢？

师生活动：教师让学生以小组为单位，通过合作学习的方式共同探寻问题的答案.图3（2）中，根据勾股定理易得S+S=2（S+S），于是学生可以将该问题转化为：图3（1）中，S+S=2（S+S）是否成立？为了让学生直观体验其中的一般规律，教师利用几何画板进行动态演示，学生通过直观观察发现以上结论成立.

设计意图：教学中，教师通过创设问题继续引导学生挖掘蕴含其中的一般规律，引导学生用数学的眼光看世界，充分体会数学的和谐美、对称美、简约美，激发学生学习数学的积极性.以上结论是通过猜想、对比、观察得到的，并未进一步验证，所以并不能作为结论，教师还应提供时间让学生利用已学数学知识进一步验证，以此让学生体会数学的严谨美.

3 突破疑难，提升能力

严谨性是数学的独特之美，任何数学结论必须借助严密的逻辑方法进行推理验证，真正做到有理有据.当然，数学公式、定理、结论等是较为抽象的，学生在证明的过程中可能会遇到一定的障碍，面对学生的障碍，教师不要急于灌输，而是要适度地进行启发和点拨，让学生通过独立思考和合作探究等方式自主探寻解决问题的方法，突破疑难，以此增强学生学习的信心，提升学生的数学能力.

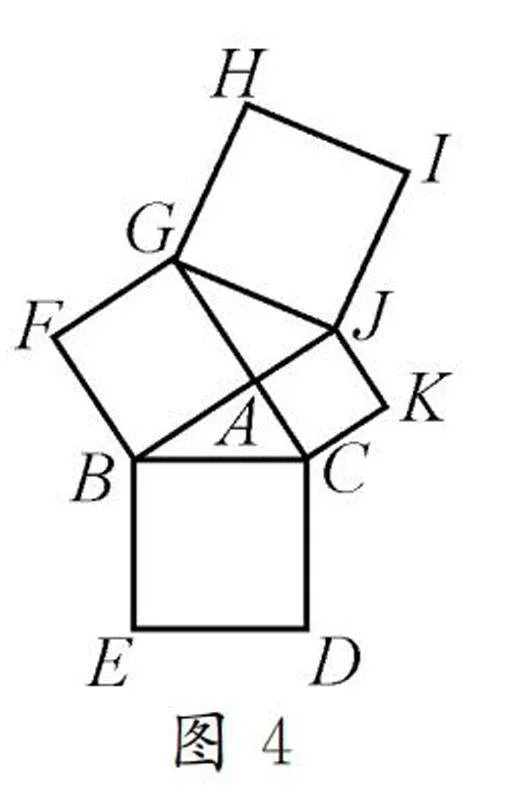
例如，以上环节中，学生通过猜想得到结论后，仅用几何画板进行验证显然是不具说服力的，为此教师要鼓励学生用数学语言来表达它，并用数学思维来思考，用数学知识来探究.在以上探究的基础上，教师继续追问：如图4，若△ABC是钝角三角形，如何证明S+S=2（S+S）？

师生活动：问题给出后，教师让学生独立证明.该问题较为抽象、复杂，很多学生感觉无从下手.为了帮助学生突破疑难，教师引导学生观察图5，并展示欧几里得证明勾股定理的过程.在这一方法的启发下，通过师生、生生互动交流，得到证明过程：

设计意图：教师引导学生利用已有知识、方法进行验证，充分感悟你增我减、我增你减的平衡美，体验数学的严谨美，点燃学生的探究热情，提升学生的数学学习兴趣.

4 结束语

数学知识具有高度的抽象性，若想学好数学，需要学生具有一定的想象力和数学抽象思维能力.教学中，若教师仅关注知识的讲授和题目的训练，很容易增加数学的枯燥感，从而导致学生产生畏难情绪，影响学习效果.因此在数学教学中，教师要善于从引导学生发现、体会数学之美的角度入手，提供时间和空间让学生去发现、体验数学的各种美，如对称之美、简洁之美、严谨之美等，感悟数学的无限魅力，提升学生的探究兴趣，从而让学生在发现美、探究美的过程中消除枯燥情绪和畏难心理，增强学生的学习信心，提高学生分析、发现和解决问题的能力，促进学生核心素养的落实[1].

在本课的教学中，教师将勾股定理相关知识进行拓展延伸，将直角三角形拓展为锐角三角形和钝角三角形，以直角三角形为基础开展一系列的探究活动，让学生用数学眼光看世界，用数学语言表达世界，用数学思维思考世界，充分体会数学的和谐美、对称美、简洁美，充分体验探究的魅力，感悟特殊到一般的思想方法，提升学生的数学能力与素养.

参考文献：

[1]田学宁.感受数学之美 提高学习兴趣[J].科技创新导报，2015，12（9）：116，118.