借助数形结合，实现算理一致性

［摘 要］ 为了借助数形结合，实现算理一致性，文章以“两位数乘两位数笔算乘法”一课为例，在教学中设计了三个环节：开门见山，直接探究计算方法；层层追问，体现乘法算理一致性；提问质疑，深化乘法算理和算法。借助数形结合不仅能帮助学生掌握两位数乘两位数笔算乘法的算理和算法，还能让学生感悟转化思想在乘法计算中的应用。

［关键词］ 算理一致性；笔算乘法；数形结合

学生在学习“两位数乘两位数笔算乘法”之前已经接触了表内乘法、两位数乘一位数的笔算乘法等内容，已经具有探究乘法算理和算法的经验，本单元的学习内容是对两位数乘一位数乘法的知识迁移。课始，教师出示生活情境中的乘法例题，让学生尝试解决两位数乘两位数笔算乘法；然后，全班学生一起交流笔算乘法的计算方法，并比较不同方法之间的相同点和不同点，体现数形结合思想和算理一致性；最后，全班学生一起提问质疑，解决更多与两位数乘两位数笔算乘法相关的问题。

一、开门见山，直接探究计算方法

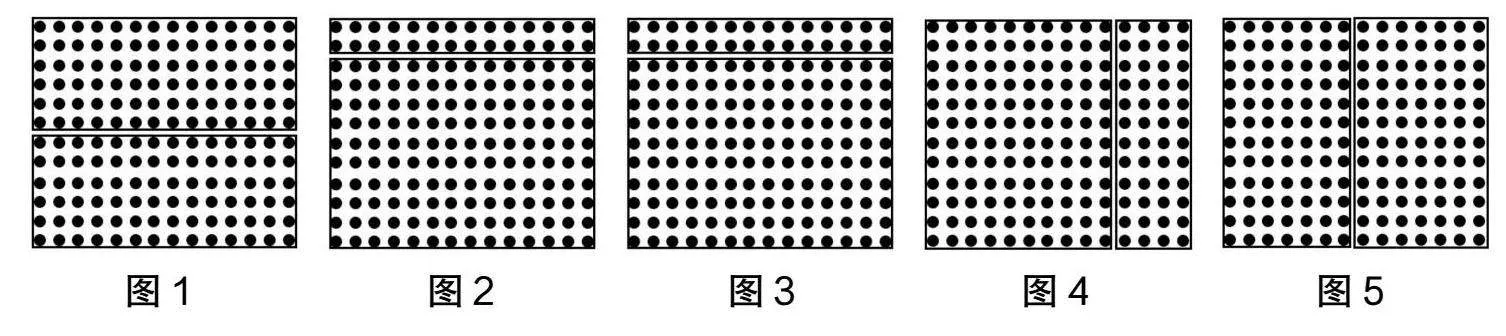
师：（出示例题：学校要在花坛里摆一些盆花，每行14盆，有12行，一共有多少盆花？）同学们，这节课我们来研究“两位数乘两位数笔算乘法”，你们能用不同的方法来探究14×12可以怎么计算吗？请你们先在点子图中圈一圈，再列式算一算。

生1：（边说边指图1）我把12分成6和6，先算上面的6个14，算式是6×14=84；再算下面的6个14，算式是6×14=84；最后把上面和下面加起来，算式是84＋84=168。

生2：（边说边指图2）我把12分成2和10，先算上面的2个14，算式是2×14=28；再算下面的10个14，算式10×14=140；最后把这两部分加起来，算式是28＋140=168。

生3：（边说边指图3）我是用列竖式的方法计算的，先用14乘12个位上的“2”，算式是14×2=28；再用14乘12十位上的“10”，算式是14×10=140；最后把28和140相加，算式是28＋140=168。

生4：（边说边指图4）我把14分成10和4，先算左边的10个12，算式是10×12=120；再算右边的4个12，算式是4×12=48；最后把120和48加起来，算式是120＋48=168。

生5：（边说边指图5）我把14分成7和7，先算左边的7个12，算式是7×12=84；再算右边的7个12，算式是7×12=84；最后把左边和右边两部分加起来，算式是84＋84=168。

评析：在新课导入和探究环节中，教师去除了过多的干扰因素，直接出示例题让学生探究两位数乘两位数笔算乘法的计算方法。从学生“拆数”的角度看，有的学生把14拆成两个相同的数，有的学生把14拆成10和4，有的学生把12拆成两个相同的数，还有的学生把12拆成10和2；从学生探究两位数乘两位数笔算乘法的书写形式看，有的学生用三个算式来表示计算过程，有的学生用列竖式的方式来表示计算过程。

二、层层追问，体现乘法算理一致性

1. 沟通计算方法之间的联系

师：刚才同学们想到这五种方法来计算两位数乘两位数的乘法，我们一起来看这五种计算方法，你们能在点子图中找到算式中的这些数吗？（学生在点子图中分别指出算式中的数）

师：我们通过点子图得到这些算式的方法，在数学上叫作数形结合。这种数学思想方法帮助我们根据直观的点子图写出抽象的算式，而且圈出来的部分和算式是一一对应的。同学们，我们观察这五种计算方法，它们有什么共同点？

生1：这五种计算方法都是把一个数拆成10和几或者两个相同的数。

生2：这五种计算方法都是把两位数乘两位数的乘法转化为两位数乘一位数的乘法，再把两个算式的结果加起来。

师：如果我们把两位数乘两位数的乘法看作新问题，把两位数乘一位数的乘法看作旧知识，就是先把新问题转化成旧知识，再利用推理的方法解决新问题。

2. 沟通不同乘法的计算方法

师：同学们，转化的方法在表内乘法、两位数乘一位数乘法中都有体现，你们找到了吗？

生3：我们在计算表内乘法的时候，是把表内乘法转化为几个相同加数的和来计算。比如5×9，我们就是用加法5＋5＋5＋5＋5＋5＋5＋5＋5=45或者9＋9＋9＋9＋9=45来计算的。

生4：我有补充，我们计算表内乘法的时候可以把要计算的乘法口诀转化为已经知道的乘法口诀。比如要计算5×9，如果我们知道4×9=36，可以利用“4个9加1个9等于5个9”得到5×9=36＋9=45；如果我们知道3×9=27，可以利用“3个9加2个9等于5个9”得到5×9=27＋2×9=45。

生5：我们在计算两位数乘一位数的时候，先拆分一个两位数，然后用表内乘法和整十数乘法来计算。比如14×3，我们可以把14分成10和4，利用表内乘法3×4和整十数乘法10×3来计算。

师：我们在计算乘法的时候，都用到了转化法。我们把表内乘法转化为已经学过的相同加数的加法，把两位数乘一位数的乘法转化为已经学过的表内乘法和整十数乘法，把两位数乘两位数的乘法转化为两位数乘一位数的乘法和整十数乘法。如果要计算三位数乘两位数的乘法，你们会怎么转化呢？

生6：我们可以把三位数乘两位数的乘法转化为三位数乘一位数的乘法和整十数的乘法。

评析：为了帮助学生体会乘法算理的一致性，教师设计了两个任务：第一个任务是沟通计算方法之间的联系，先引导学生比较点子图与算式，渗透数形结合的思想方法；再引导学生比较五种方法之间的联系，引出转化思想；第二个任务是沟通不同乘法的计算方法，引导学生用转化的观点来看待表内除法、两位数乘一位数的乘法和三位数乘一位数的乘法等，促使学生在比较中感受算理一致性。

三、提问质疑，深化乘法算理和算法

师：同学们，我们知道了两位数乘两位数笔算乘法的计算方法，你们还有什么疑问吗？四人小组先交流一下。

师：（投影展示学生的问题）刚才老师收集了同学们的一些问题：第一个问题是交换两个乘数的位置，积是否会变化？第二个问题是加法的计算方法是相同数位相加，乘法的计算方法为什么不能相同数位相乘呢？第三个问题是怎么快速判断两位数乘两位数乘法的积到底是几位数？同学们，请先在小组里想一想这三个问题，你们能解决这些问题吗？

生1：我们小组解决了第一个问题，认为交换两个乘数的位置，积不会变化。比如两位数乘两位数23×12=276，交换两个乘数的位置就是12×23=276，所以它们的积是不变的。

生2：我们小组解决了第二个问题，认为乘法的计算方法是不能用相同数位相乘的。比如两位数乘两位数45×19=855，如果是相同数位相乘就是十位乘十位40×10=400，个位乘个位5×9=45，这样45×19=400＋45=445，计算结果是错误的。

生3：我们小组解决了第三个问题，认为可以通过估算快速判断两位数乘两位数乘法的积。比如，65×53肯定是四位数，我们可以把65估计成60，把53估计成50，两个数都小估后是60×50=3000，所以这个算式的积肯定比3000要大，一定是四位数；28×29的积肯定是三位数，我们可以把28估计成30，把29估计成30，两个数都大估后是30×30=900，所以这个算式的积肯定比900小，一定是三位数；37×29的积不能判断，我们可以把37估计成40，把29估计成30，两个数都大估后是40×30=1200，所以不能判断这个算式的积是三位数还是四位数。

评析：俗话说：“学贵有疑，小疑则小进，大疑则大进。”这句话告诉人们在学习过程中要不断反思学习过程和学习结果，从而不断质疑学习过程并提出新的问题，再寻找新问题的解决方案，促进数学知识的深度学习。本节课中教师巧妙地安排了提问质疑的环节，引导学生围绕“两位数乘两位数笔算乘法”这个主题提出新问题并解决这些问题，帮助学生深刻地理解和掌握笔算乘法。

总之，在运算教学中教师不仅要教学计算方法和算理，还要帮助学生沟通前后相关知识的联系与区别，促进学生认识到算理一致性。比如，乘法计算都可以利用数形结合思想让抽象的竖式与直观的图示进行一一对应，计算过程都是通过拆分一个数把新问题转化为旧知识。