立足“自主视域”，精设小学数学课堂“探究任务”

［摘 要］ 立足“自主视域”，精准设计数学课堂“探究任务”，要求教师从“学标”“学情”“学理”出发，设计结构性任务、层次性任务、表现性任务。精准设计“探究任务”赋予学生充分的自主学习的时空，能引导学生从自身数学学习的“现实水平”提升至“可能水平”。

［关键词］ 小学数学；自主视域；探究任务；精准设计

建构主义学习观认为，学生的数学学习是学生的自主、能动、有意义的建构。在小学数学教学中，教师要立足于促进学生数学“自主性学习”立场、视角，即立足于“自主视域”开展数学学习。实践证明，立足“自主视域”的任务驱动教学法是一种有效的教学方法、策略。“任务驱动教学法”是以“任务”为核心开展的教学。教师要精准设计任务，有效应用任务，充分发挥任务的导学、驱动功能，彰显任务的导学、驱动价值。

一、从“学标”出发，设计“结构性任务”

学习目标（以下简称为“学标”）是学生数学学习的原点和归宿。教师精准设计“探究任务”，应当从学生的“学标”出发。“学标”不仅具有指向性、针对性，还能激发学生数学学习兴趣，调动学生数学学习积极性；“学标”不仅指向学生的认知，而且指向学生的情感、态度等；“学标”往往具有统摄性，能有效指导、规划、设计学生的数学学习。依托“学标”、依据“学标”，可以设计“结构性任务”。

“学标”让学生的任务驱动有了自主的根基。在小学数学教学中，学生可以聚焦“学标”、依托任务开展基于“自主视域”的探究性学习。比如教学“分数的意义”这一部分内容时，笔者引导学生以一个物体、一个计量单位、许多物体组成的整体为对象，引导学生平均分。通过平均分的操作、画图等活动，让学生自主建构“分数的意义”。因此，笔者根据“认识单位‘1’的量”“理解分数的意义”“培育学生的抽象、概括、归纳能力”等学习目标，设计了层次性、结构性的任务。

任务1：将一个苹果、一块月饼平均分给2个人，每人分得多少？

任务2：将一盒饼干、一盒粽子平均分给3个人，每人分得多少？

任务3：抽象、概括出单位“1”，归纳分数的意义。

任务4：认识分数单位，认识分数中有多少个这样的分数单位。

这样的任务设计完全围绕着学生的目标而开展。这样的任务不仅围绕着学生的“学标”而开展，而且具有结构性。在结构性任务中，学生既可以按部就班地按照任务设定的顺序来开展自主性学习，又可以小组为单位分别对“任务1”和“任务2”开展研究。“任务1”和“任务2”既是层次性、阶梯性的任务，又是并列性的任务。“任务1”“任务2”与“任务3”之间形成了一种递进性，即前一个任务往往是后一个任务的基础，后一个任务是前一个任务的延伸、拓展和提升，是前一个任务的升华。当学生完成了“任务1”“任务2”后，自然能概括单位“1”，进而完成对分数的意义的自主性、自能性建构。这样的结构性任务既有明显的分级特点，是递进性的；又是相互补充的，是并列性的。任务都指向分数的意义建构，都指向促进学生对分数的意义的多维理解。

“学标”是探究性任务设计的导航仪，也是探究性任务设计的方向盘。因此，教师在教学中要精准解读教材，把握数学学科知识的本质与关联。只有从“学标”出发来精准设计任务，才能让任务真正地驱动学生的数学学习、导引学生的数学学习，让学生的数学学习有效、高效。

二、从学情出发，设计“层次性任务”

精准设计探究性任务时，教师要了解学生的具体学情，把握学生的认知规律、认知水平，从而让任务能切入学生数学学习的“最近发展区”，让学生能“跳一跳摘到果实”，让学生的认知能从“现实水平”过渡、提升、发展至“可能水平”。从学生的具体学情出发，就是让任务与学生的已有知识经验链接。

从学生的具体学情出发，本身就是立足于学生的“自主视域”。实践证明，从学生的“具体学情”出发，设计“层次性任务”，能有效引导学生的层次性探究，让学生的数学学习能拾级而上、不断进阶。比如在“圆的认识”一课教学中，笔者在课前与学生的访谈中把握了具体学情：有的学生认为图形是直线图形，都是由线段围成的；有的学生知道有曲线图形，比如圆，但对于圆的认识停留在感性的、直观的层面，认为由弯曲的线围成的图形就是圆。笔者在教学中从具体学情出发，设计了层次性任务，引导学生逐步完成对圆的结构性、整体性的建构，将圆的诸多的、零散的知识点集结在一起。

任务1：小红家离学校2千米，小红家的位置可能在哪里呢？

任务2：怎样画圆呢？徒手画，借助实物画，还是用工具画？用圆规为什么能画出圆？

任务3：将画好的圆剪下来对折，折痕有什么特点？在圆内画半径，看谁画的半径多？

这样的“任务”设计，能精准化学生的数学探究，让学生的数学思维、认知逐步得到提升。“任务1”能激发学生的数学学习兴趣、调动学生的数学学习积极性，让学生对小红家的位置可能在哪里形成积极的猜想，从而在学生的头脑中建立“到定点的距离等于定长的点的轨迹的集合”的表象；借助“任务2”，从圆的形成、创造上引导学生认识、理解、感悟圆的特征，引导学生认识圆的半径的特质、直径的特质等；借助“任务3”引导学生探究圆的各部分的特征，探究“圆的半径和直径之间的关系”等。这样的任务设计看似非常简单，却是一个关系性的整体，能有效引导学生进行精准化的数学探究，让学生将相关知识系统化、结构化，帮助学生建构完整的数学知识结构、认知结构等。

三、从学理出发，设计“表现性任务”

“学理”是学生数学学习的内在理由，它不仅决定着学生的数学学习内容、要求、目标等，而且决定着学生的数学学习方式。从“学理”出发，教师要精心设计“表现性任务”，借助“表现性任务”有效引导、驱动、激励学生的数学学习，让学生的学习信息得到及时的、有效的反馈。教师要积极回应学生的数学学习信息反馈，并根据反馈信息对学生的数学学习进行“再评价”。

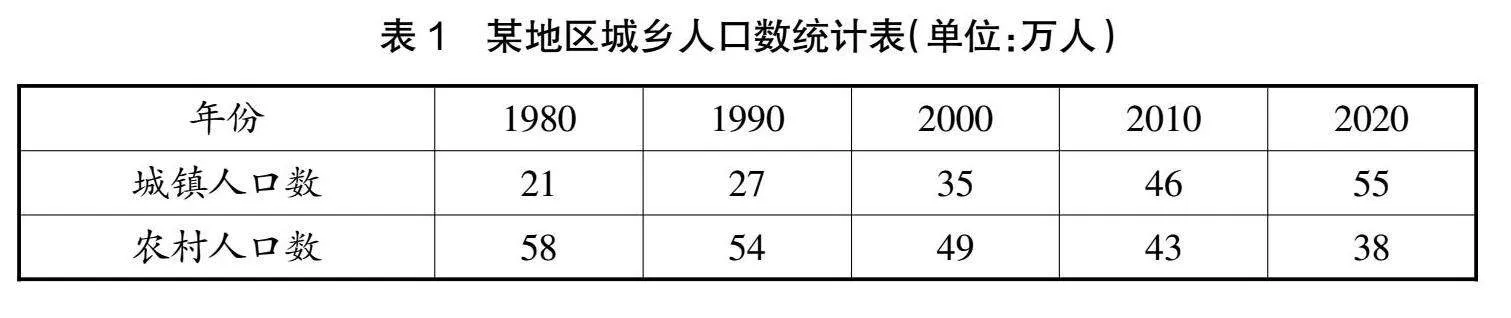
表现性任务不仅能帮助学生精准调控学习进程，让学生优化学习方式，而且能兼顾学生的数学学习差异，从而让学生的数学学习走向个性化、个体化。教师在设计表现性任务的时候，要兼顾学生的差异性，鼓励学生进行个性化探究。比如教学“复式条形统计图”时，笔者先给学生提供了一个统计表（见表1），然后根据这一部分内容的特质，设计了3个表现性任务。

任务1：根据表格中的数据特点，你准备制成什么统计图？为什么？

任务2：请你制作一张复式条形统计图，并标注相关的统计图的要素；

任务3：请你对复式条形统计图进行评价，它与单式条形统计图的区别在哪里、优势在哪里？

这样的表现性任务能有效引导学生的数学思维，促进学生进行精准性探究。在表现性任务的驱动下，学生开展积极的数学“再创造”，从而让学生的数学学习真正回归生活、回归真实、回归创造。表现性任务可以前置，让学生学在教之前；可以中置，让教为学生的学服务；也可以后置，引导学生反刍，让学生的学为教师的教释义。

立足“自主视域”，精准设计数学课堂“探究性任务”，要求教师成为学生数学学习的研究者、组织者、参与者。在教学中，教师要研究数学学科知识的本质、关联，要把握学生的具体学情，了解学生的数学学习主要方式、特质等；要从学标、视角、学理的视角精准设计“探究任务”，从而让“探究任务”高效发挥引导学生探究的功能、作用，让“探究任务”不仅成为学生数学学习的载体、媒介，还成为学生数学学习的驱动、引擎。实践证明，教师精准设计的“探究任务”赋予了学生充分的自主学习的时空，能引导学生从自身数学学习的“现实水平”提升至“可能水平”。