在“旧”中重构 在“新”中提升

［摘 要］ 在小学数学复习教学中，“炒冷饭式”的做法不利于提升学生学习能力和发展学生思维。基于此，教师应认真研究教学、研究学生，从整体和全局的角度重新出发，将旧知识、旧练习从“新”呈现，以此提高学生参与课堂的积极性，促进学生的思考，提升复习教学品质。

［关键词］ 复习课；旧知；重构；新知；提升

“复习课难上”是教师的共识。部分教师在复习课上或是引导学生进行知识点罗列，或是重复做过的题目，把复习课看成“昨天故事的重现”，导致学生参与课堂的积极性不高，教学效率低下。虽然复习课的知识点是旧的，练习的内容是旧的，但是教师可以从形式上、视角上、方法上进行调整，从“新”出发，给学生以焕然一新的感觉，以此充分发挥复习课的价值，提高复习课的品质。那么教师在教学中如何做到从“新”出发呢？笔者以“多边形的面积计算”复习课为例，谈谈对“新”的理解与感悟。

一、旧词新译，译出本质

师：本章我们学习了多边形的面积计算，相信大家对如何计算了如指掌，对“面积”一词你们是如何理解的？如果把“面积”这两个字分开来看，你们想到了什么？

生1：看到“积”我想到了乘法。

生2：这些就是“面”。（学生用摸的动作表达“面”）

师：将“面”和“积”合在一起可以怎么理解呢？

生3：用乘法计算“面”的大小。

生4（补充）：用乘法计算物体或平面图形有多少个面积单位。

师：很好。平面图形的面积与线段的长度有何关联呢？

生5：线段的长度就是看线段中包含多少个长度单位，这是可以直接测量的；平面图形的面积是平面图形中有多少个面积单位，可以用乘的方式来计算。

师：说得很好，相信通过重新解读，大家对“面积”有了新的认识。

教学思考：教师在复习教学中若一成不变地将相关概念、公式等重复一遍，会让学生感觉枯燥、乏味。为了改变这一局面，教师在“旧词新译”环节引导学生换个角度重新认识“面积”，这样既有旧知线段的长度串联，又为后续体积的学习奠定了基础。

二、旧知新联，联出体系

师：想一想我们已经学习了哪些平面图形的面积？它们的计算公式你们还记得吗？

师生共同归纳总结相关的面积公式后，教师提出要求：

（1）任选一个图形，说一说它的面积计算公式是如何推导的？

（2）这些平面图形的面积计算公式存在怎样的联系？请用合适的方式进行整理归纳。

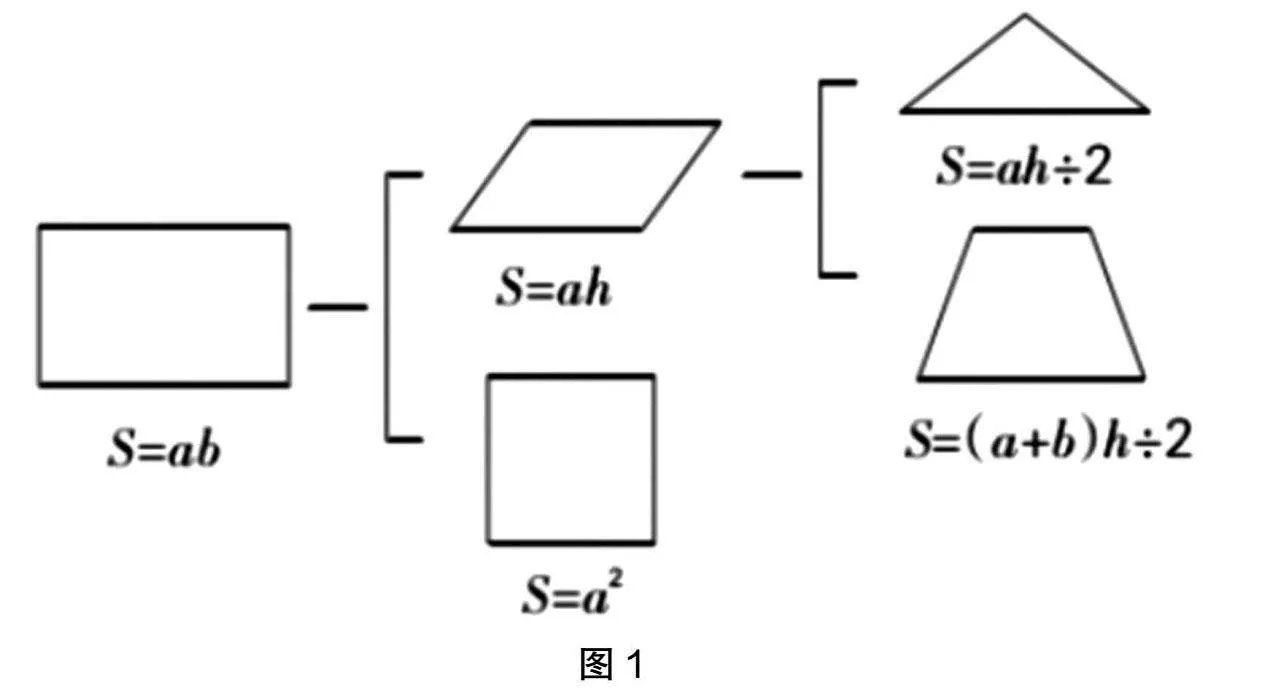
问题给出后，教师让各小组充分交流，并采用适合的方式进行整理归纳，以此将零散的知识以框架图的方式加以呈现，逐渐形成知识体系。教师课件展示学生的汇报结果（如图1）。

师：现在请各小组派一名代表具体说一说平行四边形、三角形和梯形的面积计算公式推导过程。

学生回答（略）。

师：大家都说得很好，它们的推导过程有何相同之处呢？

生1：都是先将图形转化为已经学过的图形，然后根据我们已经会求的图形的面积公式来计算。比如，平行四边形转化为长方形，三角形转化为平行四边形。

师：很好，大家将“转化法”用得很熟练，转化是我们研究数学问题重要的数学方法。

师：大家整理面积计算公式的顺序与教材所呈现的顺序是一致的，都是从已经学过的长方形面积出发进行整理。现在我有一个想法：如果换一个方向，从梯形开始研究，会是怎样的结果呢？

师：试想一下，若将梯形的上底延长，会是怎样的结果？（学生积极思考）

生2：它可能就变成长方形。

师：还有其他可能吗？

生3：还可能是平行四边形。

师：很好，如果将梯形的上底缩短，又会怎么变化呢？

生4：当梯形上底的两点变成一点时，它就变成了三角形。

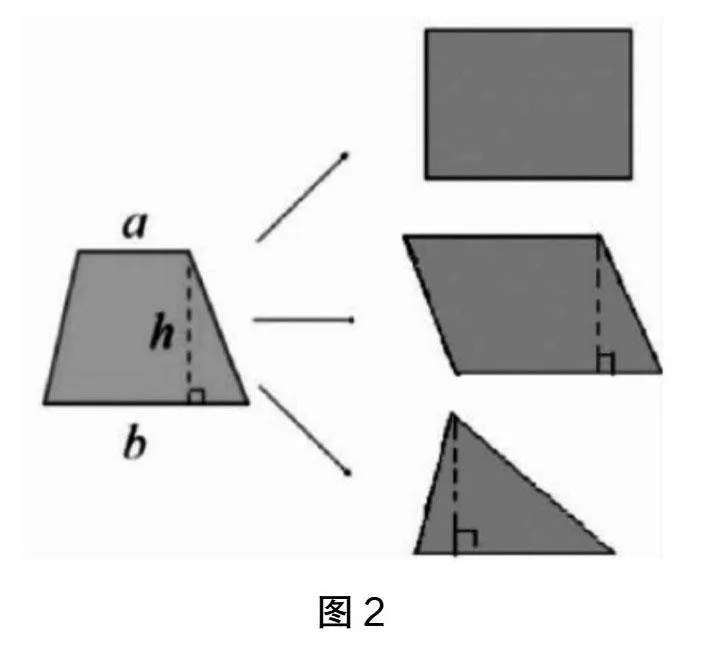
师：看来大家有着超强的想象力，我们一起见证一下，看一看会不会变成大家所说的图形呢？（教师动态演示变化过程，如图2）

师：从梯形出发，转化成其他图形时，梯形的上底、下底和高发生了怎样的变化？能否用梯形的面积计算公式来求其他三个图形的面积呢？

生5：当梯形转化为长方形或平行四边形时，它的下底和高不变，而此时的上底与下底相等，所以有S=（b+b）h÷2=bh。

生6：当变成三角形时，下底和高不变，此时的上底为0，所以有S=（b+0）h÷2=bh÷2。

师：太棒了，从梯形的面积计算公式出发，也能推导出其他三个平面图形的面积，太神奇了。

教学思考：随着知识储备、学习能力的不断提升，学生的理解能力也会不断提升，因此复习教学中教师不能简单地进行知识的罗列。在复习阶段，教师要着眼全局，引导学生关注知识间的内在联系，帮助学生建构个体认知体系。在上述环节中，教师先是引导学生根据自己的认知整理平面图形面积计算公式间的联系，然后从“新”出发，引导学生从梯形开始建构，通过联系与整理将看似孤立的面积计算公式串联在一起，形成一张知识网。

三、旧题新做，做出能力

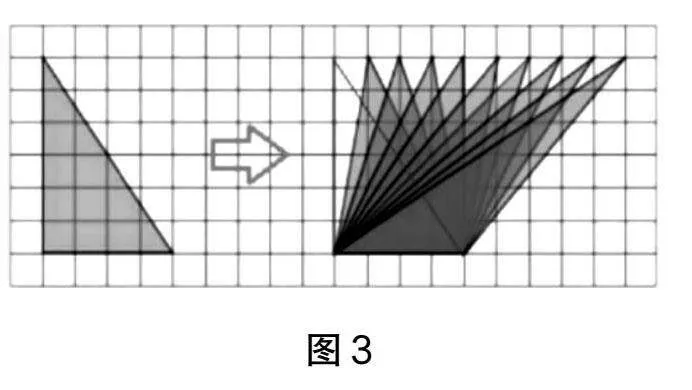
师：孙悟空无意间得到了一个直角三角形，他闲来无事，就把这个三角形“变变变”。（教师动态演示变化过程，如图3）

师：请大家从数学的角度分析一下，孙悟空是如何给这个直角三角形变形的？

生1：每次将直角三角形的一个顶点向右平移1个格子。

师：认真观察这些三角形，在顶点向右平移的过程中，什么变了？什么始终没有变呢？

生2：三角形的形状变化了，但是底和高的长度始终没有变。

师：很好，那么根据不变的特性你们发现了什么？

生（齐声答）：三角形的面积不变。

师：很好！现在我们继续观察图4，你们有什么发现？（教师隐去多余的图形）

生3：图4是图3的变形，隐去了多余的三角形，只留下两个三角形。

师：很好，观察得非常仔细。从数学的角度进一步分析，看看你们得到了什么？

生4：图4中颜色较深的部分形状不同，不过它们的面积相同。

师：哦！请具体说一说。

生5：其实颜色深的三角形的面积就等于两个大三角形的面积减去那个公共的三角形面积。通过上面分析知道两个大三角形的面积相等，这样它们同时减去同一个小三角形的面积，剩下的面积自然是相等的。

师：观察得很仔细，推理得很严谨，非常棒！

师：如果在面积保持不变的基础上继续变变变，你们还有其他好办法吗？（学生积极动手画图研究，很快就有了答案）

生6：可以把底和高都变一变，比如底变成6格、高变成4格。

接下来学生给出其他变形方案，比如将底变成8格、高变成3格；底变成12格，高变成2格等。这样通过再次变化图形，促进了学生对面积公式的深化理解，培养了学生思维的灵活性和变通性。

教学思考：练习在复习课上必不可少，它是将知识转化为能力的必经之路。在复习课上，教师不能将那些见过的、讲过的题目直接搬出来，而是要将其改头换面，换个角度或换个方式来呈现，通过横向拓展和纵向延伸来激发学生探索的热情。在本环节教学中，教师从等底等高变形开始，引导学生在变化中寻找不变的特征，促进了学生的思考，提高了学生的注意力。

复习课的内容虽然是旧的，但是若将其“改头换面”，它们依然能够打动人心，依然能够激发学生探究欲，让学生通过对“旧内容”进行感悟后有新的收获、新的发展。