借助“形”和“数”，建构周长概念

［摘 要］ 特级教师牛献礼在“认识周长”一课教学中利用“形”和“数”结合帮助学生建构周长概念，通过指和说帮助学生理解周长的内涵，通过测量帮助学生计算图形的周长，通过“一分为二”策略帮助学生辨析图形周长。

［关键词］ 认识周长；教学片段；数学概念

周长即“一周”的长度：“一周”存在于封闭图形的边沿上，“长度”需要学习者用直尺等测量工具去度量。因此，“一周”是度量的对象，“长度”是度量的结果。在特级教师牛献礼的“认识周长”数学公开课上，全班学生在他的循循善诱下从封闭图形的“面”上剥离出周长的“形”，通过明确度量对象“边线”的方式理解了周长的“量”和周长的数学本质［１］。

一、在指和说中理解周长的内涵

1. 在“三指”中认识数学课本的周长

师：今天我们要学周长，同学们之前听说过吗？你们认为周长是什么意思？

生1：我认为周长就是一个图形，为四条线的长度，如果图形有缺口就不是周长。

生2：我觉得周长并不是只指一个图形，它是指所有的封闭图形。只要是封闭图形，都可以算出它的周长。

师：什么叫封闭图形？

生2：没有开口的图形就叫封闭图形。

生3：周长是指一个图形边缘一共的长度，即使是凹凸形状、封闭的图形也叫周长。

师：摸一摸数学书的封面，你们能指出这个封面的一周在哪里吗？

生4（边指边说）：从数学课本的这里开始，然后一直往下到这里就拐过来，最后回到起点，正好重合了。

师：拿起你的数学书找一个起点，指一指这个封面的一周，边指边说从哪里到哪里。（学生动手指封面的一周）

师：必须从这个点出发吗？从这个点出发到这个点是一周吗？老师把数学课本的封面图片放到电脑屏幕上，观察从这个起点出发，正好绕了一圈，用数学的语言表述就叫一周。这一周中红色边线的长度叫作周长。（板书：封闭图形一周的长度叫它的周长）

师：同学们，我们再拿起这本数学书，先仔细地摸一摸这本数学书的封面，再指一指这个封面的一周，边指边说它是什么。（学生动手指封面的一周）

2. 在辨析中理解面和周的区别

师：我们把数学书封面的字、颜色、花纹都去掉，你们觉得“面”和“一周”有区别吗？区别在哪儿？

生5：我觉得周长是它的一周，是指红色的线段；面是它的面积，是指蓝色部分这一块。

生6：我觉得一周是空心的，不包括里面部分；面是实心的，是指里面部分。

生7：我觉得可以把“面”假设为一块土地，这一块土地的大小就叫它的面积；外面的红线，我假设它是土地旁边的一条线，这条线的长度叫一周。

师：这个比喻很形象，把“面”比作一块土地，外面的线就好像是土地外面围的栅栏。

生8：一周就好像外面的一个保护线，面就是指里面的犯罪现场。

生9：如果没有这个面，就没有它的一周长度。

3. 在比画中寻找量角器的周长

师：老师还带了一个量角器，它的形状是半个圆，谁能指出量角器正面的一周在哪儿？

生10（边指边说）：先从量角器的起点出发，沿着直的线，再向上弯回到起点。

师：老师把量角器的字、颜色、花纹都去掉，数学书封面的一周和量角器的一周有什么相同点和不同点？

生11：它们都有一个起点和终点。

生12：相同点为它们的一周都是空心的，它们的面都是实心的。不同点为数学书是直的，量角器有一个地方是弯的。

赏析：在这个教学环节中，牛老师从“形”的角度帮助学生理解“什么是一周”，让学生能用自己的语言正确描述或指出一个平面图形的周长。牛老师通过对学生进行调研分析发现：（1）学生对“周长”的认知并不全面，他们对周长概念的数学本质的认识存在偏差。比如有的学生认为“一周”就是指一星期有7天，有的学生认为曲线无法测量等。（2）学生在观察一个图形时对“面”和“周”容易混淆，他们对“周长的本质是线段长度”的认知也有困难。（3）学生对“周长是图形所有边长的总和”这个认识有困难，有的学生认为图形的曲线不是边，因此认为圆形等图形没有周长。为了突破“认识周长”教学中的重难点，牛老师先借助学生熟悉的数学课本，让他们三次边指边说数学课本的周长，加深他们对“封闭图形一周的长度叫作周长”这个数学概念的理解；再从具体的生活实物中抽离出边线的数学模型，引导学生辨析“面”和“一周”的区别，发现“一周”是存在于面上的线段，为后面测量和计算图形的周长做好铺垫；最后，牛老师通过让学生找量角器的周长，帮助学生理解封闭图形的一周，让学生看到弯弯的曲边也是有长度的，因此量角器是有周长的。

二、在测量中计算图形的周长

1. 计算直边图形的周长

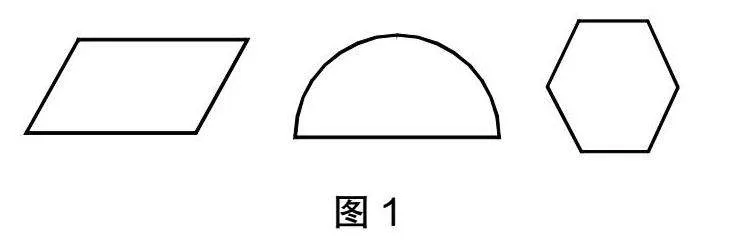
师：如图1，任选一个图形先量一量它的边长（取整厘米数），再列式计算它的周长。什么叫整厘米数？

生1：整厘米数指的是整数。比如，量的时候会有误差，如果量得比2厘米多一点，就把它看成2厘米；如果量得比3厘米少一点，就把它看成3厘米，把测量结果看成与它接近的那个整数。

师：老师教你一招，可以在边的旁边写上长度，这样就不会忘记。谁来说一说计算了哪些图形的周长？

生2：我算了平行四边形的周长，先量出每条边的长度，上下两条边的长度都是3厘米，左右两条边的长度都是2厘米，所以周长是（2＋3）×2=10（厘米）。大家有问题吗？

生3：你量过一条线段后，怎么知道对面的一条线与它一样长？

生4：我觉得它们是对称的，再量一量就知道了。

生5：我用直尺量出每条边的长度分别是2厘米、3厘米、2厘米、3厘米，周长是2＋3＋2＋3=10（厘米）。

生6：我计算了六边形的周长，先量出一条边是1厘米，六边形的每一条边都是一样长，所以1×6=6（厘米）。大家还有问题吗？

生7：你为什么敢确定它们是一样长的？如果下面的两条边稍微长一点点，你就算错了。

生8：我们再量一量就可以了。

2. 计算曲边图形的周长

生9：我算了半圆形的周长，先量出这个弧形的一半，差不多是2厘米，所以整个弧形是4厘米；再量出下面一条横线是3厘米，周长是4＋3=7（厘米）。大家有问题吗？

生10：你刚才量的是这个半圆形的半径，怎么知道那条弧线的长一定是4厘米？

师：她虽然量得不对，但是这个错例给了我们启示，不能用直尺量出弧线的长。对此，同学们有好办法吗？

生11：我们可以用软尺量出弧线的长。

生12：如果你有一根毛线的话，可以先在弧线上固定一个点，把这根毛线沿着弧线绕完整个半圆形；再用直尺量出这段毛线两个点之间的长度。

赏析：在这个教学环节中，牛老师从“量”的角度帮助学生掌握“一周有多长”，让学生能根据周长的意义通过测量和计算等基本方法求出一个平面图形的周长。周长存在于封闭图形的面上，它是一个“形”；它是指封闭图形一周的长度，也是一个“量”［２］。因此，牛老师在教学周长计算时分为两个层次：第一个层次是直边图形的周长，学生在计算平行四边形和正六边形的周长过程中，发现图形的周长是把图形一周的每一条边的长度相加。这时，牛老师引导学生提问“怎么知道对面的一条线与它一样长”，培养了学生的严谨思维。第二个层次是曲边图形的周长，这是学生认知过程中的难点。牛老师通过让学生计算半圆形的周长，引导学生暴露错误思考，让学生在思考中发现可以用软尺或毛线测量半圆形的曲边，同时让他们发现在计算半圆形周长时还要加上一条直直的边。通过计算这两类图形的周长，学生对“周长是封闭图形一周所有边线的长度总和”有了清晰的认知。

三、在“一分为二”中辨析图形周长

师：画一画，在下面的长方形里画一条线，把长方形分成两个图形，使分成的两个图形的周长相等，可以怎样画？同学们能想出几种不同的画法？老师给你提供了四个长方形，结果有可能比四种少，也有可能比四种多。如果长方形不够了，自己可以在旁边添加长方形，然后画出来。

生1：第一种，沿着宽的中点横着画一条线；第二种，沿着长的中点竖着画一条线；第三种，沿着左上到右下画一条对角线；第四种，沿着右上到左下画一条对角线。

生2：我有补充，在左上角顶点向右边和右下角顶点向左边取相同长度的两个点，把这两个点连起来。

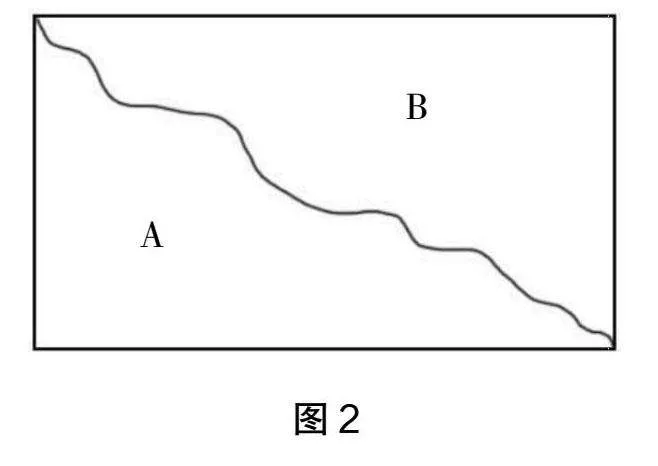
师：老师受到这位同学的启发，画了一条弯曲的线。如图2，把长方形分成了A和B两部分。这两部分的周长一样吗？

生3：它们的周长是一样的。A的周长是一横一竖一弯，B的周长也是一横一竖一弯。一横一竖是一样长，一弯是相同的，所以A和B的周长是一样的。

赏析：在这个教学环节中，牛老师从培养能力和发展素养的角度引导学生探索“把长方形一分为二”，让学生能应用周长的含义进行较复杂图形的判断和推理，并解决数学问题［３］。“把长方形一分为二”，这是一个低起点的开放题，既能让不同水平的学生都参与到这道数学题的思考过程中，也能让学有余力的学生创造出更多的不同画法。在汇报交流中，学生一开始想到的是沿着宽的中点画、沿着长的中点画、沿着对角线画等常规画法，在不断深入思考中发现从上边和下边取长度相同、从左边和右边取长度相同、任意曲线连接对角线等创意画法，由此得出这道开放题有无数种做法的结论。同时，牛老师引导学生从周长的角度比较A和B这两部分周长相等的原因，又一次加深了学生对“周长是封闭图形一周所有边线的长度总和”这个周长的数学本质的理解。

总之，在概念教学中教师不仅要让学生知道概念的含义，还要让学生具有理解概念的能力，并在具体情境中运用这个概念解决实际问题。这个学习过程是让学生从原来的知识识记到创造应用的过程，也是培养学生数学核心素养和提升学生数学思维能力的过程［４］。牛老师精心设计的“认识周长”一课，让学生经历了回忆与再现、问题解决与应用、思维迁移与创造等过程。这个教学过程蕴藏着大量的数学思维，教师要通过一次次激发学生的数学思维，帮助学生从“形”和“数”的角度建构起周长的数学本质，促进学生区分“周长”和“面积”这两个数学概念。

参考文献：

［１］ 殷如意，刘文，杨传达. 基于问题学习 发展核心素养——以“圆的周长”教学设计为例［Ｊ］. 小学数学教育，２０２２（１２）：１２－１３，２０.

［２］ 汤倩. 数学实验：彰显数学学习魅力——《圆的周长》教学片断与赏析［Ｊ］. 小学教学设计，２０２２（２３）：６２－６４.

［３］ 周婷婷. 浸润数学文化课堂，汲取学科核心素养——《圆的周长》教学实践与思考［Ｊ］. 数学之友，２０２２，３６（１５）：４１－４３，４７.

［４］ 解海霞. 问题重组 融会贯通——“圆的周长”教学实践与反思［Ｊ］. 中小学数学（小学版），２０２２（０９）：３７－３９.