基于“平均分”思想的“归一问题”教学探究

［摘 要］ “归一问题”一直是小学数学教学重点和难点，小学生对一些无现实模型支撑的“归一问题”感到困惑和难以理解。教师可以基于“平均分”思想引导学生分析思考，帮助学生直观理解和解决此类问题，使学生在学习过程中理解解决问题背后的数学原理，提高学生的数学学习效果和兴趣。

［关键词］ “平均分”思想；“归一问题”；等分除法；包含除法

数学中的“归一问题”是小学数学教学中的重要内容，也是小学生数学学习的难点。“归一问题”要求将一个整体按照一定的比例或关系分成若干份，探索每份的数量或比例。学习这类问题，学生不仅能够培养比例思维和分数运算能力，还能够提高解决实际问题的能力，发展数学综合素养。这类问题还涉及不同单位和数量的转换及比较，且相关比例内容的学习在小学知识结构上相对滞后。学生虽然学习了比，但是不会通过比例关系解决问题，导致解决问题的效果不佳。因此，如何让学生有效地学习“归一问题”，是数学教学中亟待解决的问题。

在实际教学中，学生相对容易理解和掌握具有现实意义并有实际模型的“归一问题”，比如根据“路程=速度×时间”求“速度”，根据“总价=单价×数量”求“单价”。对于一些无现实模型支撑的“归一问题”（如“菜籽榨油”问题），学生感觉比较抽象，无法分析和解决问题。下面，笔者以“菜籽榨油”问题为例，探讨利用“平均分”思想来解决这类问题，帮助学生更直观地理解和解决此类“归一问题”，并在教学过程中引导学生理解问题背后的数学原理，提高学生的数学学习效果和兴趣。

一、教学引入

1. 问题呈现

如果10千克菜籽可以榨4千克油，求1千克菜籽可以榨油多少千克？榨取1千克油需要菜籽多少千克？

2. 问题分析

学生初看这个问题会有点懵，心中充满疑惑：题目中的菜籽和油都是以“千克”作为数量单位，它们能不能相除？如果可以相除，那么如何解释其实际意义？用谁除以谁呢？因此，如何帮学生消除疑惑，理解题意，师生共同分析解决问题是教学的关键。

3. 问题解决

人们在分物的时候常常要求做到“公平”，在“分”的时候每个人要“分”得同样多，也就是每份分得同样多，这种分法叫平均分。“平均分”是分物时所用的一种思想方法。从学生视角看，“平均分”是有形的，对正处于直观形象思维阶段的小学生来说，理解“平均分”的难度不大。

首先，教师可以引导学生思考问题的实际意义，即将一定数量（千克数）的菜籽按照一定对应关系榨出相应数量（千克数）的油；然后，通过“平均分”思想的引导，将总量分成若干等份，每份量的大小即为所求。教师可以和学生共同进行这样的分析：如图1所示，在“1千克菜籽可以榨油多少千克”问题中，“1千克菜籽”占“10千克菜籽”的，就是把“10千克菜籽”平均分成10份，每份量为1千克菜籽。那么“1千克菜籽”可以榨油多少千克呢？那是把“4千克油”也平均分成10份，每份油为4÷10=0.4，所以1千克菜籽可以榨油0.4千克。其中的“4”代表“油的总量4千克”，“10”代表“油的份数10”。（4÷10并不是两个相同单位的量相除）因此，结果单位和被除数单位一致。

以此类推，如图2所示，在“榨取1千克油需要菜籽多少千克”问题中，“1千克油”占“4千克油”的，也就是要把“4千克油”平均分成4份，这样每份量为1千克油。那么榨取“1千克油”需要多少千克菜籽呢？那肯定是把“10千克菜籽”也平均分成4份，每份菜籽量为10÷4=2.5，所以榨取1千克油需要菜籽2.5千克。其中的“10”代表“菜籽总量10千克”，“4”代表“菜籽份数4”。这种分析解决问题的方法是基于“平均分”思想（等分除法），紧扣“单一量”，将“归一”法很清晰地展现出来，学生容易理解其中的道理，能够更深层次地体会到前后知识之间的联系，即知其然，又知其所以然。

4. 原理分析

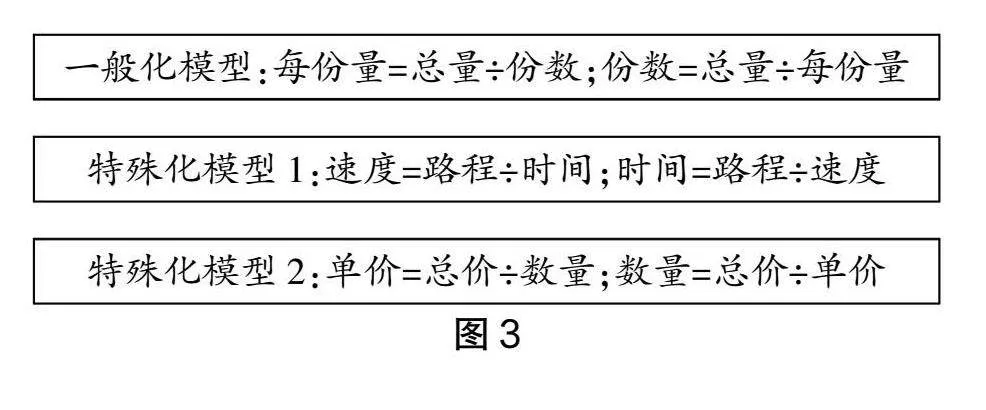
“平均分”思想的原理是将一个整体按照一定的份数进行等分，然后求出每一份的大小，或者已知平均分的每一份的大小求份数。这种方法的优势是简单和直观，不需要进行复杂的换算和运算，只需要采用简单的除法，根据等分除法或包含除法就可以得到答案。这种方法的局限是需要保证总量、份数和每份量都是整数，否则会涉及小数的除法，会增加难度和误差。为了说明“平均分”思想的原理，教师可以引导学生用“平均分”模型的数学表达式来辅助说明：“平均分”模型的数学表达式为“每份量=总量÷份数”或“份数=总量÷每份量”。教师引导学生将此模型与“路程=速度×时间”模型、“总价=单价×数量”模型（如图3）进行对比，“平均分”模型实质是这两种实际模型的一般化形态，由此让学生更好地理解“平均分”模型的意义。

二、教学拓展

在解决问题的过程中，教师可以引导学生对问题进行拓展与深化：如果10千克菜籽可以榨4千克油，照这样计算，3千克菜籽可以榨油多少千克？榨取5千克油需要菜籽多少千克？

先分析第一个问题：要求3千克菜籽可以榨油多少千克，可以根据“平均分”模型求出1千克菜籽榨油=4÷10，那么3千克菜籽榨油=4÷10×3=1.2（千克）；还可以根据“平均分”模型求出榨取“1千克油”需要菜籽=10÷4，那么3千克菜籽榨油=3÷（10÷4）=1.2（千克），这里要用到“包含除法”。

再分析第二个问题：要求榨取5千克油需要菜籽多少千克，可以根据“平均分”模型求出1千克菜籽榨油=4÷10，那么榨取5千克油需要菜籽=5÷（4÷10）=12.5（千克），这里要用到“包含除法”；还可以先根据“平均分”模型求出榨取“1千克油”需要菜籽=10÷4，那么榨取5千克油需要菜籽=10÷4×5=12.5（千克）。

在以上问题中，菜籽和油的数量都是整数，如果数量是小数如何用“平均分”模型来理解呢？比如，如果5.2千克菜籽可以榨2.08千克油，求1千克菜籽可以榨油多少千克？按照上述的理解，将“2.08千克油”平均分成5.2份，所以1千克菜籽榨油=2.08÷5.2=0.4（千克）。这时，学生有点懵了：平均分成5.2份？这个怎么理解啊？此时，教师可以引导学生把“菜籽量”和“油量”都扩大100倍来进行考虑，将原题变成“如果520千克菜籽可以榨208千克油，求1千克菜籽可以榨油多少千克”，这样根据“平均分”模型得出1千克菜籽榨油=（2.08×100）÷（5.2×100）=0.4（千克）。教师引导学生将这个解答方法与解答“2.08÷5.2”相对照，让学生理解被除数和除数同时扩大100倍后，根据商不变的规律，结果保持不变。

三、教学反思

“平均分”思想方法和除法的两种含义（等分除法和包含除法）紧密联系，学生对“平均分”思想方法理解并不困难。因此，教师引导学生用“平均分”思想来认识“单一量”的本质，用“平均分”模型来解决“归一问题”，可以让学生回到问题的原点，从本原性上思考这类问题。

在教学中，教师可以通过实例演练来巩固学生的理解，可以设计一些类似的问题让学生独立思考，让学生根据不同的情况选择合适的方法来解决。教师还可以引导学生进行反思，思考解决问题的方法是否通用，是否存在更简便的解决方法。比如，教师可以让学生思考“平均分”模型与“路程=速度×时间”模型、“总价=单价×数量”模型的异同及联系；可以让学生探讨一下“菜籽榨油”过程中各数据之间究竟存在怎样的数量关系，为什么会有这样的关系；还可以引导学生理解“教学拓展”中“照这样计算”的含义。这样可以激发学生的思维和创造力，让他们能够在不同的情境下灵活运用数学工具去探究数学的奥秘。通过这样的实践与反思，学生可以不断提高解决问题的能力，并且加深对数学原理的理解。

综上所述，基于“平均分”思想解决“归一问题”具有很好的效果，它能够帮助学生更直观地理解并解决问题，提高学生的数学理解能力和应用能力，为学生后续学习比例内容作铺垫；同时激发学生的学习兴趣，培养学生的思维能力和探究习惯。在小学数学教学中，教师要重视基于“平均分”思想的教学方法帮助学生更好地理解和应用数学知识，通过不断地引导学生思考和实践，让学生不仅能掌握解决问题的方法，还能深入理解方法背后的原理。