结构化教学数量关系，助力高段学生有效解决问题

［摘 要］ 数学解决问题离不开数量关系的探索、分析和应用。研究者从学科本质和学生学习需要的角度分析和统整数量关系主题的相关内容，进行有关联的、结构化的教学实践，避免学生孤立、碎片化地学习知识和方法，以实现学生知识与方法的迁移，形成与发展学生的核心素养。

［关键词］ 数量关系；结构化；核心素养

数量关系是提高学生发现和提出问题、分析和解决问题能力以及培养模型意识和应用意识的重要载体。《义务教育数学课程标准（2022年版）》（以下简称新课标）将“数与代数”领域的内容整合为“数与运算”“数量关系”两个主题，第一次明确提出数量关系主题教学，并特别提出要设计体现结构化特征的课程内容。新课标在内容组织上呈现明显的结构化特点，学科一致性也得到体现，要求教师对“数量关系”内容进行整体建构和进行结构化教学，帮助学生完善认知体系，发展学生思维能力和核心素养。

一、高段学生对“数量关系”理解情况调查

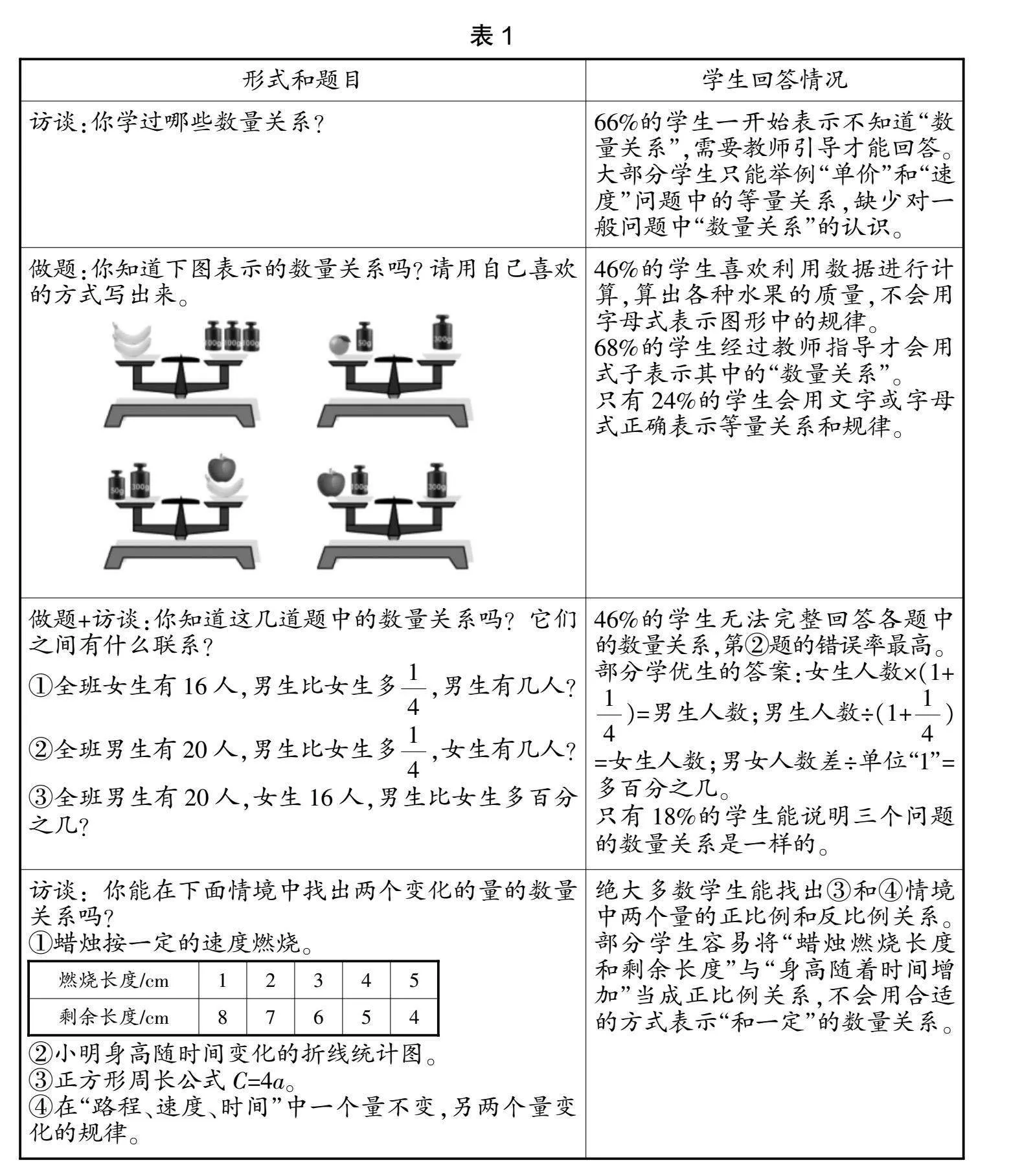
为了了解高段学生对“数量关系”的认识和理解，笔者对本校六年级50名学生进行了学情调查，调查情况见表1。

通过以上调查，笔者发现学生在“数量关系”的学习上存在一些问题。

1. 数量关系理解片面化

原有教材除了在四年级“常见数量关系”教学中和五年级方程教学中明确提出“数量关系”，其他时候只是在个别习题中提出过。部分教师和学生以为只有某几e977b5d38da7fcc795e276f1067f334b类例题（如天平、方程、正反比例等）才存在数量关系，将数量关系作为一种特殊题型的专题训练，缺乏在一般问题中分析数量关系的习惯。

2. 数量关系学习碎片化

学生的思维仍处于算术思维或不稳定的代数思维阶段。解决不同问题时，学生喜欢将问题中的未知数作为数量关系式的结果，比如求速度时使用数量关系式“路程÷时间=速度”，求时间时使用数量关系式“路程÷速度=时间”等。这种“程序性知识点”加重了学生的学习负担，说明他们缺乏结构性的数量关系表达和分析能力。

3. 数量关系应用浅显化

高段问题包含较为复杂的数量关系，需要学生综合运用所学的知识和方法，特别是运用数量关系模型及其拓展模型去分析和解决。大部分学生在解决复杂问题时虽然能找到相应的数量关系，但是不会用合适的方式表达，如文字、画图、表格、关系式、字母式等，缺乏深入的应用和拓展能力，这是他们学习的难点。

二、建构数量关系体系，提升解决问题的能力

在数量关系主题内容教学时，教师要将其作为一个整体来理解，以模型作为数量关系的核心概念，以建立各学段不同内容之间的联系。

1. 知识系统化，构建数量关系整体认知

吴正宪在《“数与运算”内容结构化问题分析与教学实践》中提出以“数量关系”为核心的问题解决可以分为三个阶段：运算意义、建立模型、用字母表示关系或规律。

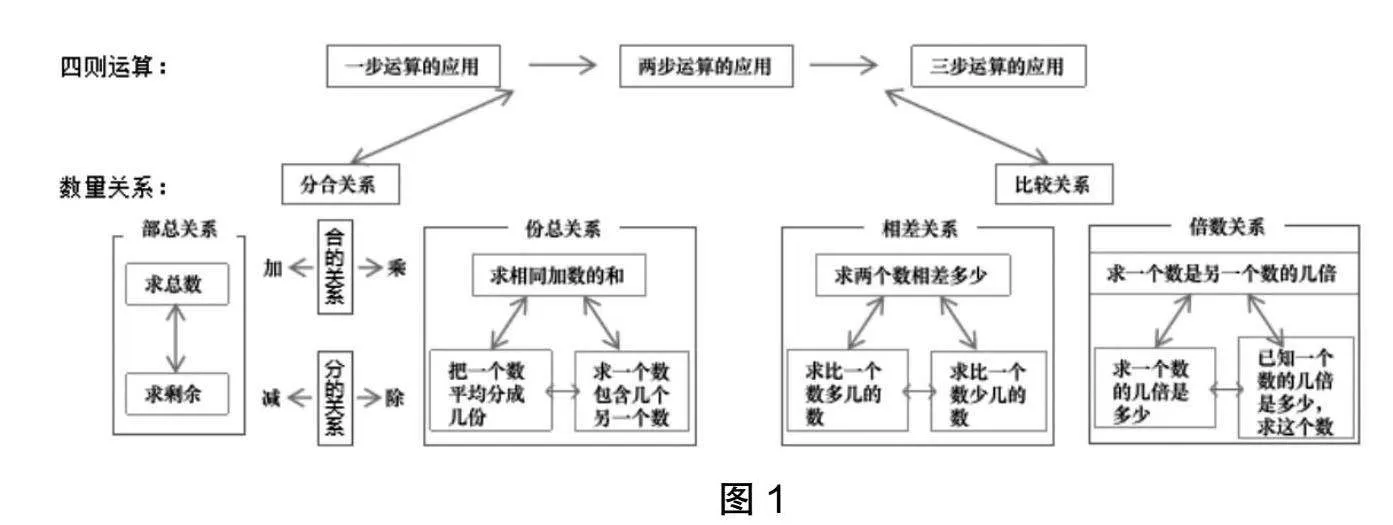
要实现知识系统化，教师既要对教材知识体系进行梳理，还要发现并揭示其内在的逻辑与关联。比如，第一学段，学生需要在理解加、减、乘、除四则运算意义的基础上，经历看图、分与合、画一画、摆一摆或说一说的过程，初步感悟数量关系。此时，教学的要点不是要求学生写出相应的“数量关系式”，而是要体验和感受分量与总量之间的关系；第二学段，学生在理解四则运算意义的基础上建立模型和解决问题，感悟速度、单价是用两个量之间的倍数关系来描述事物的属性，加法模型和乘法模型是解决问题的常用数学模型；第三学段，教学的重点是数量关系模型的拓展应用，重点是学生对数量关系的分析与判断。教师可以把数量关系的结构与运算本身的结构相整合，进而厘清数量关系的主体脉络（如图1）。

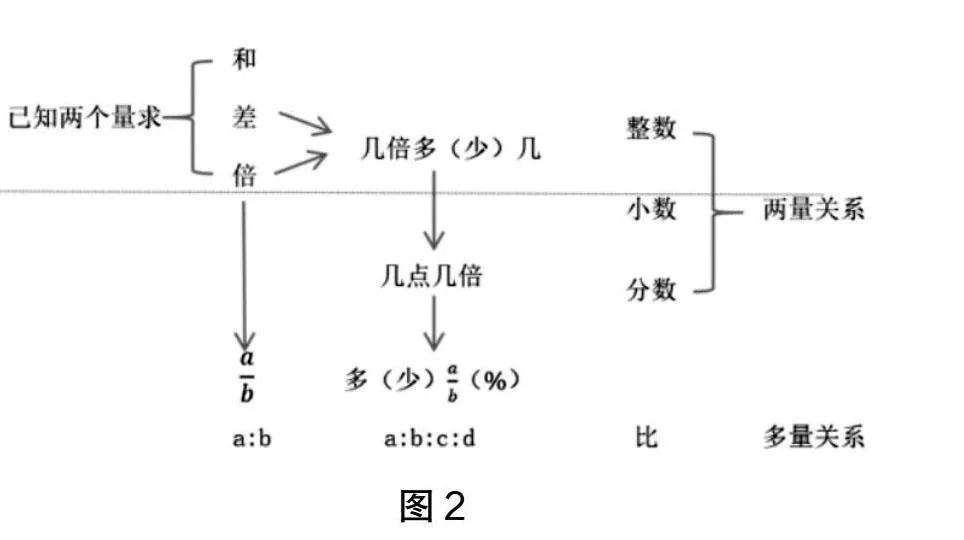
随着数的认识扩展到小数、分数，则两个量的非整数倍就可以用小数、分数（百分数）或比来表示（如图2）。

这样的内容结构体系虽然无法全面覆盖所有小学的数量关系（如正、反比例关系以及两积之和关系等），但是知识结构化有助于教师更关注知识层面上的全景建构，让学生充分感受和体验“数量关系”的意义，把握知识结构、方法结构，提升数学素养。

2. 教学结构化，培养数量关系分析意识

学生解决问题时经常直接列式计算，缺乏分析数量关系的过程，导致求解复杂问题时错误百出。比如，数量关系“多与少”的学习，对于问题“小明有15个苹果，比小红少3个，小红有几个苹果”，学生错误率经常过半。这些“已知比较量，求标准量”的逆运算模型是学生学习的薄弱点，产生了“单位‘1’已知就用乘法算式，单位‘1’未知就用除法算式”这样不科学的思维模式。

学生在列式解决问题前一定要养成数量关系分析的过程，如图3。为培养数量关系分析意识，教师要引导学生进行训练。

（1）无问题式的数学信息加工训练

教师出示没有问题的数学信息，让学生关注信息加工过程。比如，“小明比小红多3个”→谁是标准量、谁多→画线段图（建议先画标准量，再画比较量）→列数量关系式：小红苹果数+3=小明苹果数。

比如，学生在学习分数问题时呈现的思维路径：“小明苹果数比小红苹果数多”→谁是单位“1”，把什么平均分成4份，另一个量是几份→画线段图（建议：先画单位“1”）→列数量关系式：小红苹果数×（1+）=小明苹果数。

（2）灵活运用加法模型和乘法模型

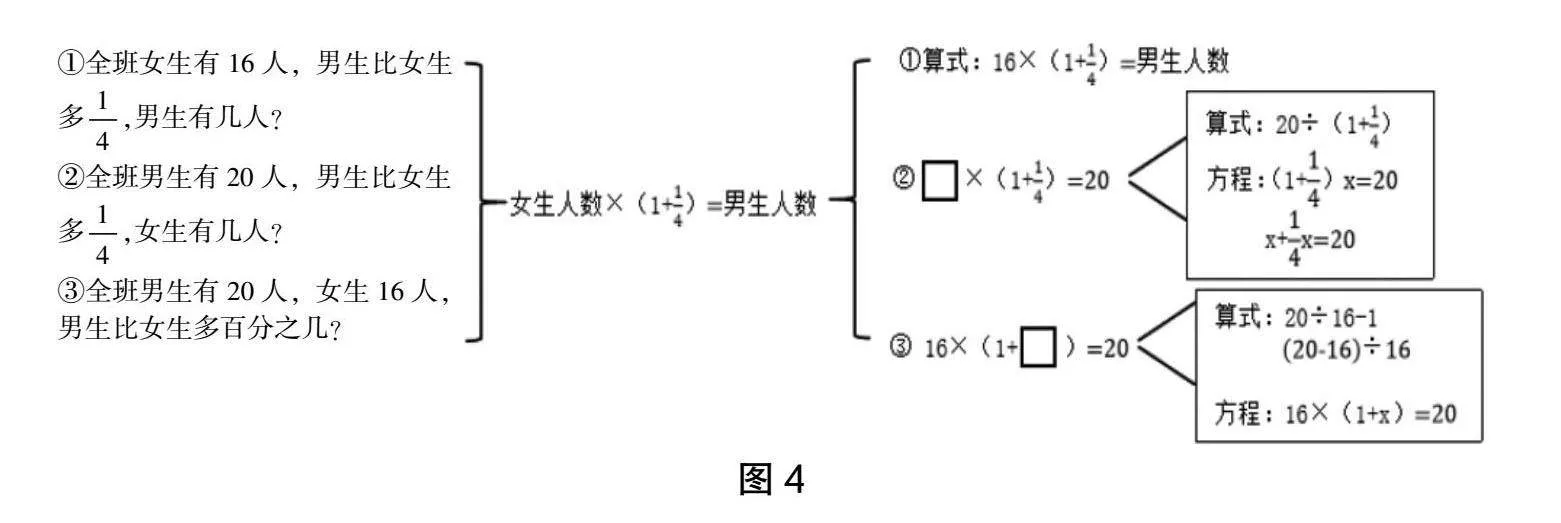
四则运算的意义是分析数量关系的基础，减法是加法的逆运算，除法是乘法的逆运算，但是学生的顺向思维多于逆向思维。为遵循学生的思维特点，在教学解决问题时教师可以把信息中的“数量关系”统一用加法和乘法模型表示出来，降低学生从具体情境中发现数量关系的难度，让学生利用四则运算的意义来思考解法。比如学情测试的分数问题可以用同一条数量关系式来统整，再利用四则运算的意义找出解法，如图4。

在统一的数量关系模型之下，为这些不同方法之间建立一座桥梁，让学生可以在更高层次的视角下关注问题中的数量关系，建构解决问题的一般模型，开放性地发展算术思维和代数思维。当然，这种结构性的方法适合复习教学或六年级教学，避免学生因未学习四则运算和方程的意义而混淆这些不同的思路。

（3）模型的拓展应用

数量关系不仅包括问题解决中的关系，也包括探索规律中的关系。数量关系不仅要找关系，还要能用含有符号的式子表达关系。这是新课标增加的内容，实际上是对数量关系的符号表达，是数学的跨领域应用和内部发展的关键。但多数情况下学生不习惯用字母式，只能粗略地表达变化规律。这需要教师在日常教学中因材施教，让学生适时进行拓展学习，体会数学符号化表示的优势。

比如，在三角形找规律的练习中，教师可以适时追问若是四边形会怎样？在学生能够迅速解决问题且兴趣正浓时，教师追问五边形、六边形、七边形……n边形情况下小棒数量和图形数量之间的关系，让学生发现用字母式比用语言、文字或图画表示的规律更加简洁清晰：x个n边形的小棒数量=（n-1）x+1。学生经历这一研究过程后，能快速求解“已知小棒数量，求能拼成几个n边形”的问题。

在日常教学中，教师可以根据学情适时地用字母式来开展教学。比如，在圆柱体积教学中，让学生利用字母式清晰表示变化情况并预测结果：圆柱的底面半径扩大2倍，体积会如何变化？V=πr2h和V=π（2r）2h。以此让学生充分经历字母式建构过程，习惯用字母式表示并解决问题，感受字母式的优势，培养符号意识与推理意识。

3. 评价一致化，提升数量关系应用能力

在解决问题的评价中，教师大多对列式计算进行结果性导向评价，很少对数量关系分析进行过程性评价，导致高段学生对数量关系的应用不充分。在结构化教学过程中，教师要通过评价来关注落实情况，让学生养成分析数量关系的习惯。

（1）评价层次量表

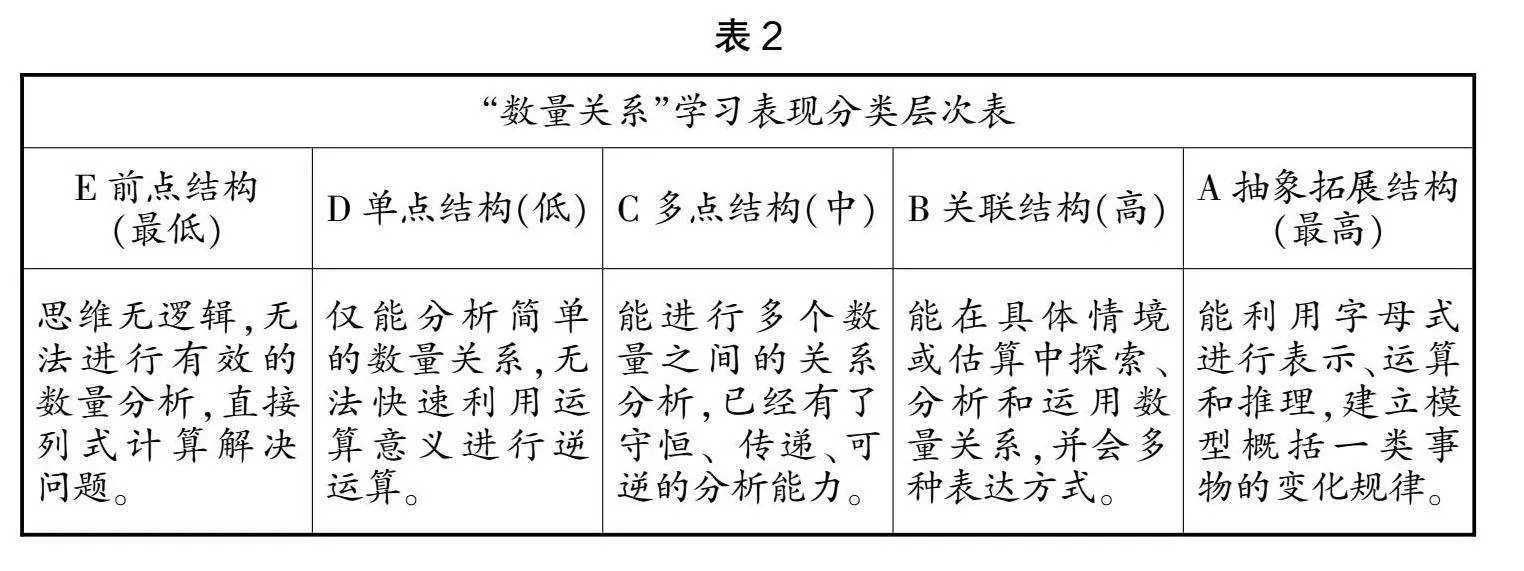
笔者根据教学内容设计了数量关系理解程度的评价层次量表，如表2。

（2）“说”出数量关系

“算”具有明显的结果导向，“说”更侧重于过程导向。教师可以从“说”的角度来评价学生的学习，让学生上台说题，利用视频记录和教师点评的方式让学生学习进步。

（3）“写”出数量关系。

评价数量关系学习情况的题型可以多样化，如画图、连线、选择等形式（如表3），以此让学生对数量关系不陌生。

三、回顾与反思

总之，在数量关系主题的教学中，教师要引导学生立足真实问题情境，经历发现和提出问题、分析和解决问题的过程，用数和符号来表达实际情境中的数量关系，并建立恰当的数学模型，实现从四则运算意义的理解到模型建立，以及解决问题从个别化到一般化，从而促进学生核心素养的发展。