大单元整体教学助力下的初中数学教学

随着教学改革的持续推进，初中数学大单元整体教学倡导教师从单元整体出发，确立单元教学目标，并依据学生的实际情况优选教学方法，提升课时教学质量，从而帮助学生构建完整的单元知识体系，促进学生数学核心素养的提升。基于此，本文以“一元二次方程”单元教学为例，对大单元整体教学助力下的初中数学教学进行探究。

一、紧跟课标，确立单元教学目标

在新课标指引下的数学大单元教学中，教师应该紧跟课标要求，对单元教材进行梳理，明确单元知识结构，同时针对学生核心素养的发展需求，确立单元教学目标，以此促进大单元教学的有效实施。

（一）教材梳理

以“一元二次方程”单元教学为例。本单元是对一元一次方程知识的延续和深化，主要内容包括一元二次方程及其有关概念、一元二次方程的解法（配方法、公式法、因式分解法）、一元二次方程根与系数的关系、运用一元二次方程分析和解决实际问题四个部分的知识。本单元是中考数学中的主要内容，在初中数学中占有重要地位。通过一元二次方程的学习，学生可以对已学过的实数、一元一次方程、因式分解、二次根式等知识加以巩固，同时又为后期学习二次函数等知识打好基础。其中，解一元二次方程的思路和方法是本单元的重点内容，也是后续学习的基础和工具。此外，学习一元二次方程对其他学科的学习也有十分重要的意义。

（二）目标确立

基于上述教材分析，足见本单元在整个初中数学知识体系中的地位和作用。结合学生学情，教师可以确立如下单元目标。

目标一：学生能从现实问题中抽象出数量之间的相等关系，并能用方程表示这种关系。

目标二：学生能认识一元二次方程刻画数量关系的意义和作用。

目标三：学生能用多种方法求解一元二次方程，体会转化思想。

目标四：学生会用一元二次方程解决实际问题，进一步体会模型思想。

二、围绕学情，优选单元教学方法

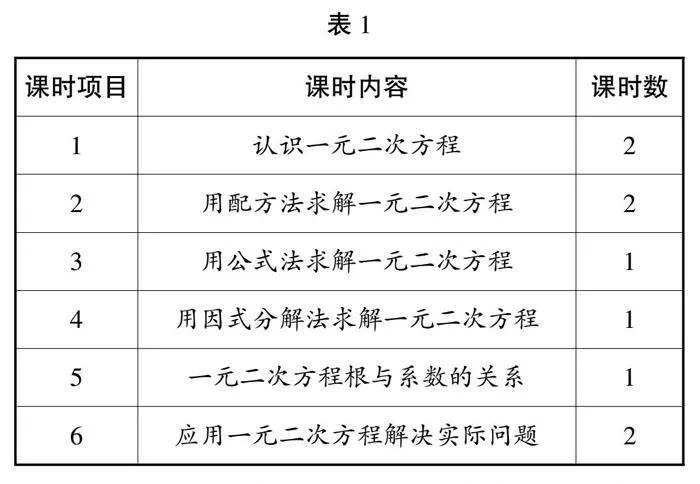
基于上述对单元教材和目标的分析，教师要根据各个课时的规划确立合理的教学方法，本单元的课时安排如表1所示。

下面以“用公式法求解一元二次方程”课时教学为例，阐述大单元教学中用到的各种教学方法，包括问题导入、合作探究、案例讲解、习题巩固。

（一）问题导入法

问题导入法，即在课程导入环节中，教师基于学生学过的数学知识，用驱动性的问题启发学生思考，引导学生对新内容形成初步认识，为后续学习作好铺垫。

以“用公式法求解一元二次方程”课时教学为例。教师首先向学生提出问题“说一说用配方法解一元二次方程的一般步骤”，引导学生回顾此前所学的配方法，为学习新知识作铺垫。

①把方程化为一般形式，且二次项系数为１；

②把常数项移到方程的右边；

③两边都加上一次项系数一半的平方；

④写成（ｘ＋ａ）2＝ｍ的形式；

⑤若ｍ≥０，两边开平方，从而得出方程的两个根。

基于学生的回答，教师继续追问：用配方法求解方程的过程比较烦琐，而且计算量大，容易出错，是否有更加简单的方式可以直接求出方程根呢？教师基于此情境问题引导学生进行思考。教师将“公式法”引入课堂，并提醒学生“如果有公式可以求解方程根，直接代数即可。”下面，我们学习用公式法求解一元二次方程。

教师通过问题给学生安排任务，鼓励学生在问题的引领下展开思考和学习，从而提高学生的学习兴趣，促进大单元教学的有效实施。

（二）合作探究法

合作探究法，即学生通过小组合作的方式，探究数学规则、数学算理的形成过程，帮助学生掌握核心知识，提升学生的数学能力，同时营造积极活跃的课堂气氛，培养学生的数学思维。

以“用公式法求解一元二次方程”课时教学为例。教师首先向学生展示一元二次方程ax2+bx+c=0（a≠0），指导学生先用配方的方法求解该方程的根。

①方程两边都除以一次项系数a得：

上述步骤是按照配方法展开的方程求解，得出的算式较为复杂，教师启发学生思考“现在可以两边开方吗？”根据配方法的规则，现在无法保证≥0，因此不能用配方法。

随后，教师指导学生通过合作探究的方式，分析什么情况下可以直接开平方。在学生小组讨论后，一致认为4a2＞0，如果要达到开方的要求，则需要≥0，只要b2-4ac≥0即可。

按照上述解方程的思路，教师指导学生假设b2-4ac≥0时，两边开平方取“±”得：x=

通过上述探究，学生明白了b2-4ac≥0是应用配方法的必要条件。基于此，教师指导学生再次通过合作探究的方式对b2-4ac的取值范围进行假设，然后求解方程的根，并鼓励学生分享自己的探究成果。

学生分享完成后，教师指导学生归纳用公式法求解方程的方法，即

对于一元二次方程ax2+bx+c=0（a≠0）

当b2-4ac≥0时，方程有两个不相等的实数根，它的根是：

x=，即求根公式。

当b2-4ac=0时，方程有两个相等的实数根；

当b2-4ac<0时，方程没有实数根。

教师通过小组讨论的方式由浅入深地引导学生学习公式法的求解方式，充分体现学生在课堂上的主体地位，让单元教学得到有效落实。

（三）案例讲解法

案例讲解法，即教师讲解课程知识相关的例题，引导学生用所学数学公式、数学定理解决问题，从而让学生由理解到掌握、由掌握到熟练应用，促进学生思维和能力的进阶。以“用公式法求解一元二次方程”课时教学为例，展示如下例题。

例1：解方程

（1）2x2+5x-3=0

（2）x2+3=2x

教师针对上述例题展开讲解，并指导学生根据教师的解题思路总结方程的解题步骤。

1.首先通过移项操作将方程化为一般形式，即ax2+bx+c=0（a≠0）

2.写出方程的各项系数和常数a、b、c各是多少。

3.求出b2-4ac的值，判断该值的大小，从而判断方程根的数量。

4.将系数和常数a、b、c代入到公式中，求方程的根。

随后，教师指导学生按照上述解题步骤自主完成下列方程的求解。

（1）2x2+3=7x （2）x2-7x=18 （3）3x2+2x+1=0

在学生完成方程求解后，教师鼓励学生上讲台按照公式法的求解步骤向其他学生展示求解的过程，锻炼学生的表达能力。如：

求解方程：2x2+3=7x

求解过程：

1.首先通过移项操作将方程化为一般形式，即2x2-7x+3=0。

2.写出方程的各项系数和常数，a=2、b=-7、c=3。

3.求出b2-4ac的值是49-24=25；判断该值的大小，b2-4ac≥0时；判断方程根的数量，方程有两个不相等的实数根。

4.将系数和常数a、b、c代入到公式中，求解方程的根，即x=，可以得出方程的根是3和。

通过例题分析，让学生在探究过程中进一步理解用公式法解一元二次方程的基本思路及步骤，培养学生的应用意识，加深学生对公式法的掌握。在大单元教学中，教师也可以根据课时重点知识引入典型例题MiZc2oA+cUkvlc7tudbHXg==，引导学生求解；同时也可以针对错题展开针对性地讲解，从而让学生规避常见的错误，提高学生的解题能力。

三、追踪过程，落实单元教学评价

在单元教学评价中，教师应该落实单元过程性评价，为教学改革提供有效的参考。仍以“用公式法求解一元二次方程”课时教学为例，教师可采用学生自评、小组互评两种方式。

（一）学生自评

在学生自评中，教师可鼓励学生在完成课时学习后及时进行反思，总结在课堂学习中遇到的问题，分析自己的弱势区，从而将自己的想法反馈给教师。为此，教师可以为学生设计如下自评单。（见表2）

（二）小组互评

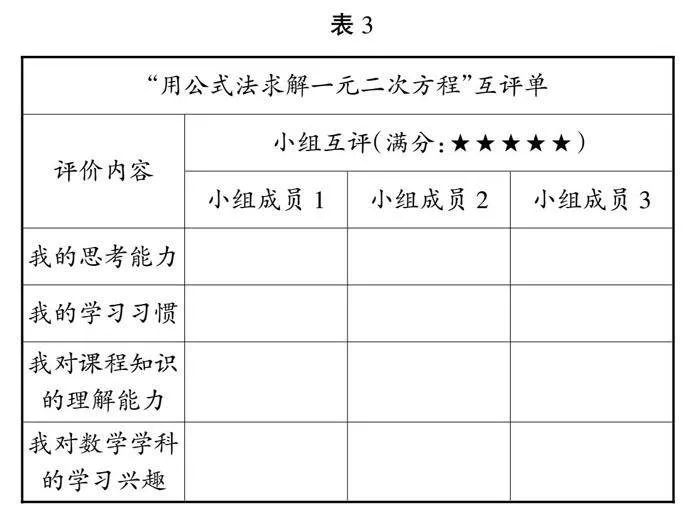
在小组互评中，教师应该始终鼓励学生积极思考、提出问题；鼓励学生对同伴在合作过程表现出来的学习能力、学习习惯、个性品质、情感态度等展开评价，并将评价结果反馈给教师。为此，教师可以为学生设计如下互评单。（见表3）

四、总结

综上所述，初中数学大单元整体教学具有非常突出的实践意义。教师要以学生为主体，紧跟课标要求，结合学生的实际情况确立单元教学目标，同时优选单元教学方法，通过多样化的教学方式提升每个课时的教学效果，培养学生的数学思维和创造力，促进学生数学核心素养的提升。另外，教师要在教、学过程中实施评价，以评促教，实现教、学、评三者和谐统一，从而促进数学大单元教学的有效实施。

（作者单位：甘肃省酒泉市新苑学校）

编辑：蔚慧敏