结构化教学：撬动高阶思维的支点

［摘 要］结构化教学彰显整体学习力量，是撬动高阶思维的支点。通过实施一致性迁移、关联性比较、思辨性对话及真实性实践等结构化教学策略，将学生的数学思维活动指向“应用”“分析”“评价”与“创造”高阶层面，助力学生高阶思维的真发生。

［关键词］结构化教学；高阶思维；小学数学

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）23-0084-03

《义务教育数学课程标准（2022年版）》（以下简称《课程标准》）强调，学生数学学科核心素养，包括用数学的思维思考现实世界，通过数学的思维形成重论据、有条理、合乎逻辑的思维品质，培养其科学态度与理性精神。数学是思维的体操，数学学习就是发展学生数学思维能力的历程。美国教育学家布卢姆提出思维活动水平的六层次框架理论，其中“记忆”与“理解”为低阶思维水平，“应用”“分析”“评价”和“创造”为高阶思维水平。高阶思维能力的培育与实现，离不开数学学习活动。培养数学核心素养需寓于单元整体教学中，同样地，高阶思维能力也需寓于结构化中。因此，教师要善于组织与设计体现结构化的教学活动，帮助学生从整体学习中进行“迁移与运用”“比较与分析”“交流与批判”和“设计与创造”等高阶思维活动。

一、讲究一致性迁移，引发高阶思维的“应用”

所谓高阶思维的“应用”，是指能利用模型或基本概念、原理在不同的情境中转换，这里的“情境转换”不是指在简单、熟知、标准情境中的“低通度”转换，而是指在复杂、陌生、开放情境中的“高通度”转换，前者属于模仿性近迁移的低阶思维，后者才属于高跨度远迁移的高阶思维。数学是一门系统性、整体性、关联性很强的学科，其中蕴含着一致性的学科本质、思想观念、核心概念，如运算的一致性、数量关系的一致性、图形的认识与测量的一致性等。学生一旦体会和把握了数学学科一致性，并能利用一致性展开迁移，就能让数学思维活动摆脱低通度的模仿与复制，实现跨情境、跨形式、跨时空的高通度迁移与转换，引发高阶思维“应用”的发生。数学知识紧密关联，在跨单元、跨年级甚至跨学段的数学知识之间存在着内在本质的一致性，这就为高通度迁移与转换提供了可能。教师要树立整体教学意识，紧密围绕反映学科本质的一致性概念，设计复杂、劣构的问题情境，展开结构化教学活动，让学生利用一致性概念去大胆迁移、探究解决，通过高通度的“情境转换”促使高阶思维“应用”的发生。

在上述教学中，教师围绕除法运算的一致性教学展开结构化教学，设计唤醒一致性经验的铺垫性习题，鼓励学生据此进行远迁移与大探索，既促进了一致性运算算理的高阶性应用，又有利于形成数的运算的大结构，彰显了高阶思维的应用意义。

二、强调关联性比较，诱发高阶思维的“分析”

所谓高阶思维的“分析”，是厘清各部分之间的关联程度和因果关系，并从中发现关系和揭示规律。高阶思维的“分析”活动，是基于感性的、整体的结构化学习材料而展开的，也就是说，在教学活动中教师要基于整体视角，引导学生发现与揭示不同数学问题之间的关系。教材的课时编排所呈现的知识是碎片化的，这样学生所习得的知识方法仅是简单地堆砌，难以从整体上厘清各个知识之间的关系，也不能发现规律，无法实现思维活动向“分析”层面的提升。因此，教师要树立大单元的整体教学观，打破教材在学科、学段及单元编排上的束缚，立足数学知识的整体结构，把握知识的内在关系，适时引入相似的、相邻的或相反的素材，设计出结构化的学习任务群，让学生展开比较、沟通、关联、重组，由此及彼地揭示关系，由表及里地发现规律，促进学生对知识的深度理解与自我重构，触发认知发展高阶思维能力。

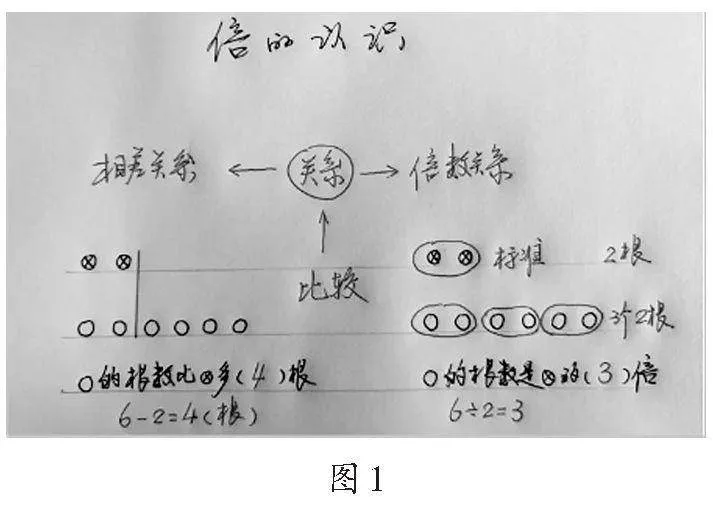
例如，在教学人教版三年级上册第五单元“倍的认识”时，江苏省名师张齐华做了如图1所示的板书设计。

不难看出，张老师不再将倍的概念作为独立的知识点来讲授，而是将其置于数的概念的整体视域中，引导学生自己去发现概念之间的内在关系。一方面，将本课的“倍”与已有的上位概念“几个几”的经验相关联，让学生比较两个量之间的关系，认识到“以一份数量为标准，另一数量里有几个这样的一份，就是几倍”，揭示了“倍”与“份”的一致性。另一方面，将倍数关系与相差关系进行对比，揭示了比较数量的两个不同维度，前者反映的是两个数量之间的包含关系，后者反映的是两个数量之间的差值关系。这样以“倍”为核心，以“几个几”“相差比较”等相关概念为依托，纵横关联、多维比较展开结构化学习，有利于学生厘清“倍”与相关概念之间的联系，让学生的思维活动从“知道是什么”的低阶“理解”层面，跃升到“揭示有什么关系”的高阶“分析”层面，认知目标也从“知道、记忆”水平提升到“揭示关联”“寻找规律”的“分析”水平，实现了高阶思维“分析”认知活动的发生。

三、组织思辨性对话，促发高阶思维的“评价”

所谓高阶思维的“评价”，是根据具体的标准或特定的目的对观点、方法、资料等作出客观判断的过程，可以看出高阶思维的“评价”活动，是学生对从事的数学学习活动进行再思考、再批判、再反省、再完善的过程，是学生由“会解答”“知结果”到“能批判、会决策”的对话过程。这与《课程标准》所提出的“发展质疑问难的批判性思维，形成实事求是的科学态度，初步养成讲道理、有条理的思维品质，逐步形成理性精神”相一致。由于学生个体间存在差异性，即使同样的问题，不同的学生理解也不同，这就使结构性思辨对话成为可能，也为“评价”的发生提供了鲜活而具体的资源。因此，在教学中，教师不应以学生能获得正确答案为目的，而要基于学科结构与学情特点，精心预设引发深度对话的结构性问题，并善于捕捉课堂上有思辨价值的结构性资源，引导学生适时驻足，开展结构性对话，如“为什么这样”“理由是什么”“还能怎样”“可以如何用”“有什么关系”等，展开指向“评价”的深层交流，实现思维的碰撞。

例如，在教学人教版五年级上册第七单元“数学广角——植树问题”时，教材先出示题目“同学们在长100 m的小路一边植树，每隔5 m栽一棵（两端都要栽）。一共要栽多少棵树？”接着，教材将题目进行简化，提出先用20 m代替100 m来检验（如图2）。

虽然大部分学生能根据简化后的题目列式“[20÷5=4]，[4+1=5]”，但却不明其理。这时，教师抓住算式中的两个“4”，借助图2追问：“两个‘4’表示的意思一样吗？”“为什么棵数要加‘1’？所加的‘1’在哪？”学生通过对话与交流，进一步认识到[20÷5=4]（段），若考虑1段与一端的1棵对应，那么4段与4棵分别一一对应；由于整条小路的两端都要栽树，所以多了1棵树，这1棵可能是最左边的1棵，也可能是最右边的1棵，所以列式为[4+1=5]（棵）。这里，教师抓住学生思维的混沌处，以两个“4”为切入点，形成具有思辨性的对话资源，据此展开辨析、操作与说理。这样，学生对植树问题背后的一一对应思想知其然且知其所以然，批判性高阶思维活动也因此得以发生。

需要指出的是，引发高阶思维“评价”发生的结构性对话资源是多样的，教师应从更广义的角度作出思考与探索。凡是可以引发学生主动对话、实现结构化思辨交流的资源，即可视为指向“评价”的好资源。例如，对已有的学习成果进行表征；对他人的发言进行补充、质疑或小结；对数学结果进行实践运用；对数学结论作出决策等，均可设计成结构化的思辨对话资源，从而引发高阶思维“评价”活动的发生。

四、开展真实性实践，触发高阶思维的“创造”

所谓高阶思维的“创造”，是将要素组合成连贯的整体，完成新模型或新结构的过程。这里的“创造”活动，强调学生使用已有的知识或经验，形成新观点、新模型或新结构，据此完成“设计任务”与“创作产品”的过程。“学”的最终目的是“用”，“学”最终需要在真实情境中，通过结构化的一系列“用”来表达与评估。在真实情境中进行项目式的结构化主题实践，更具有时空的开放性、问题的挑战性、过程的复杂性和成果的独特性，更可体现高阶思维“创造”水平的成效。从这个意义上来说，聚焦结构化主题，创设真实情境引导学生进行学科实践，是触发“创造”活动最为核心、最可物化的引擎器。为此，数学教学要聚焦结构化主题，从学生熟悉的现实生活、社会经济、科技发展等真实情境入手，设计结构化、系列式的问题展开教学，以提高学生适应社会生活的本领，彰显高阶思维的“创造”魅力。

例如，在教学人教版六年级下册“用比例解决问题”后，教材出示了一道习题（如图3）。

可以看出，这仅是一道条件完整、答案唯一的低阶思维习题，教师可通过改编，设计成以“学校升旗台旗杆有多高”为主题的跨学科实践作业，助力学生“创造”思维的发生。

教师播放视频，介绍天安门广场上更换旗杆的相关信息：1949年开国大典时所用的旗杆，高22米；1991年5月1日重新修建了国旗旗杆，高度达32.6米。随后提问：“我们学校的国旗旗杆多高呢？该如何测量呢？请设计出研究方案，并开展项目式学习实践（如图4）。”

这样，将一道简单的习题拓展为真实情境下的实践探究，让学生经历“设计方案—户外实践—交流成果—拓展延伸”的结构化学习活动，有利于学生经历问题的“发现—提出—分析—解决”的过程，学会运用数学知识解决日常生活问题，并获得“利用真实情境检验模型、修正模型，形成物化成果，包括项目产品、小论文或研究报告等”的数学活动经验，培育了学生的数学核心素养和高阶思维的“创造”能力。

总之，高阶思维能力的培养应寓于结构化的整体性教学中。教师要落实好“设计体现结构化特征的课程内容”这一课程理念，通过一致性迁移、关联性比较、思辨性对话及真实性实践等结构化教学策略，将学生的思维活动水平引向“应用”“分析”“评价”与“创造”的高阶层面，助力其高阶思维的真发生，进而培育学生的数学核心素养。

［ 参 考 文 献 ］

[1] 陈春辉.布卢姆认知目标新分类学在小学高段阅读教学中的应用研究：以H市S小学为例[D].哈尔滨：哈尔滨师范大学，2024.

[2] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[3] 黄毕年.大概念：让高阶思维真正发生[J].小学数学教育，2023（Z1）：14-16.