数学微故事辅助数学模型“曲成”

［摘 要］利用数学微故事辅助教学，通过激趣发问、演一演、画一画、建立模型、模型“曲成”五个学习活动，多元辅助，帮助学生探索、建构数学模型，从而提高他们的数学学习质量及积极的数学学习情感体验。

［关键词］数学微故事；数学模型；排队问题

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）23-0075-03

新课程改革以来，一线教师在课堂教学中致力于培养学生的数学核心素养，特别是在解决问题的教学中，着重培养学生的模型意识，但传统小学数学解决问题教学多采用讲授式方法，学生只能机械地记解题口诀、数量关系式等，缺少对数学建模的探索过程，因此学习效果不理想。《易经》中说“曲成万物而不遗”，意思是，任何事物的发展都不是一条直线，而是迂回往复的。因此，“曲成”指的是多方设法使有成就。同样地，老子也提出“曲则全”。在解决问题教学中，教师应用数学微故事辅助数学模型的“曲成”，是探索式、发现式的学习方式，符合学生的年龄和认知特点，迂回往复、多元辅助的方式助力数学模型的建构，提高学生的数学学习质量。

一、数学微故事辅助的内涵和数学建模的作用

（一）数学微故事辅助的内涵

童话故事在为儿童提供娱乐的同时，也启发儿童认识自我，并推动其人格发展。大卫·苏泽在《教育与脑神经科学》表明，镜像神经元不仅能够使个体模拟他人的行为，还能感应与此行为相关的属性，具有“移情”与“同情”功能，使得儿童在听故事或看书时会把虚拟的情节与现实生活联系起来。因此，在教学中，教师可以从学生出发，根据教材知识特点设计一个短小精悍、积极向上的数学故事，制作成3～5分钟的微视频，即数学微故事。应用数学微故事辅助课堂教学，教师要提供学习探究的材料、创设符合教学内容的情境、提出引发学生探究兴趣的问题、设置蕴含数学思想与方法的“迷思”、设计渗透德育思想且积极向上的故事情节。

（二）数学建模的作用

数学模型是用数学语言概括地或近似地描述现实世界事物的特征、数量关系和空间形式的一种数学结构，数学建模，即建立此类模型的全过程，其实质是一种深入探索的学习活动。数学建模大致有以下几个步骤：理解问题的实际背景，明确要解决什么问题，属于什么模型系统；分析和简化复杂的情境，确定必要的数据；建立模型，如数量关系式、图形等；基于模型解答问题。在此过程中，学生依据自身已有的知识和经验主动建构，有利于他们提升主体意识。在建模活动中有更大的自主性和想象空间，增强应用数学的意识，提高分析问题和解决问题的能力，有助于学生在数学学习中领悟知识的深层次含义，提高数学学习效率。

二、数学微故事辅助数学模型“曲成”的教学途径

“曲成”中的“曲”字是非常妙的，数学学习也正是呈螺旋上升的。通过数学微故事辅助教学，可以创设适合教材知识的基于现实世界的真实情境，激发学生的学习兴趣。数学模型的“曲成”顺应学生的认知规律，培养数学核心素养，提高学习效率。笔者以人教版教材一年级上册“20以内的进位加法”单元“排队问题”教学为例，探究数学微故事辅助数学模型“曲成”的实施过程。

（一）传统的“排队问题”教学

1.“排队问题”常见题型

“排队问题”是一年级数学的学习重点，常见的题型有“小明前面有5人，后面有4人，队伍一共有多少人？”“从前面数小明排第6，从后面数小明排第5，队伍一共有多少人？”“从前往后数小明排第6，后面还有4人，队伍一共有多少人？”3种。

2.学生解决“排队问题”时的常见错误

学生常见错误有4种：遗漏计算“参照物”；重复计算“参照物”；不能正确选择运算方法；列式正确但计算结果错误。

3.传统“排队问题”教学常用方法

传统“排队问题”的教学，教学方法太过机械、单一，教师直接教授“画图法”，或直接让学生记相应的做题口诀，比如“前有5人，后有4人”的口诀是“前+后+1=总人数”，“从前数排第5，从后数排第4”的口诀是“前+后-1=总人数”，“从前往后数排第5，后面还有4人”的口诀是“前+后=总人数”。

部分学生图也画了、口诀也记了，但没有经历解决“排队问题”的数学建模过程，没有真正构建解决“排队问题”的数学模型，还是不能正确解决“排队问题”。而让学生机械套用公式计算“排队问题”，不利于发展学生的创新意识和分析、解决问题的能力。

（二）数学微故事辅助数学模型“曲成”的实施过程

传统的学习观强调知识的准确性，情境是被剥离在外的，学生获得的知识是独立于具体情境的抽象、空洞的符号组合，去情境化的学习是造成学生在知识应用时缺乏灵活性的原因。应用数学微故事辅助“排队问题”的数学模型“曲成”，用故事创设情境，通过激趣发问、演一演、画一画、建立模型、模型“曲成”五个学习活动，激发学生的数学学习兴趣、探究内驱力，多方设法、多元辅助，从形象到抽象，螺旋上升建构解决“排队问题”的数学模型。

1.故事为引，激趣发问

应用数学微故事辅助课堂教学，通过故事创设情境、提出合适的问题，激起学生的兴趣和求知欲。

上课伊始，播放数学微故事《迷糊兄弟分桃》。故事内容为马小飞来到数学思维城堡，遇上迷糊兄弟在争吵，一个说桃子不够分，另一个说桃子够分。马小飞询问后知道，智慧老人给迷糊兄弟15个桃子，让他们分给练习舞蹈的迷糊妹妹及小伙伴们，并说：“迷糊妹妹排队练习舞蹈，她前面有6人，后面有8人；迷糊妹妹从前面数排第7，从后面数排第9。15个桃子够分吗？”迷糊弟弟说：“迷糊妹妹前面有6人，后面有8人，6+8=14，14<15，15个桃子够分。”迷糊哥哥说：“迷糊妹妹从前面数排第7，从后面数排第9，7+9=16，16>15，15个桃子不够分。”

视频播放到这，教师板书课题，并提出问题：“迷糊妹妹及小伙伴们排队练习舞蹈，到底一共有多少人？”学生有的说14人，有的说15人，也有的说16人，面对不同的答案，学生产生疑惑，并对“排队问题”产生了兴趣，很想一探究竟。

2.故事为媒，演一演

情境表演符合小学生的年龄特点，是学生喜欢的课堂活动之一。学生在情境表演活动中创造，在体验中学习，在愉快的情境中开启数学思维，突破思维困境，而在课始所导入的故事是很好的表演素材。

为了把抽象的题目内容表现出来，帮助学生更好分析问题，教师组织学生演一演“迷糊妹妹及小伙伴们排队练习舞蹈”的故事情节，并组织学生数一数台上表演的学生人数，发现一共有15人。教师提问：“迷糊弟弟列式计算6+8=14（人），为什么我们数一数后，数得15人？”学生回答：“14加上迷糊妹妹1人就是15人。”

教师再次组织学生演一演，扮演迷糊妹妹的学生说：“我前面有6人（6位学生出列），我后面有8人（8位学生出列），站成一排。”通过演一演，动态展示排队总人数是队伍中前面、后面和中间三部分的人数相加，符合加法模型，还直观凸显“6+8”要“+1”的缘由。最后组织学生说一说算式6+8+1=15中每个数字表示的意思，联想到前面的演示，学生明白“6”表示迷糊妹妹前面的人数，“8”表示迷糊妹妹后面的人数，“1”表示迷糊妹妹，“15”表示排队的总人数。此环节加深学生对加法算式意义的理解，帮助学生感知、理解列加法算式解决“排队问题”的模型。

3.故事为介，画一画

数学课堂上的绘画是一种重要的学习方式，是思考和探索数学知识的手段，学生通过绘画促进思维外显，将抽象的数学概念转化为具体形象；增强逻辑思维，帮助建构数学问题的逻辑结构、分析问题和找到解决方法。

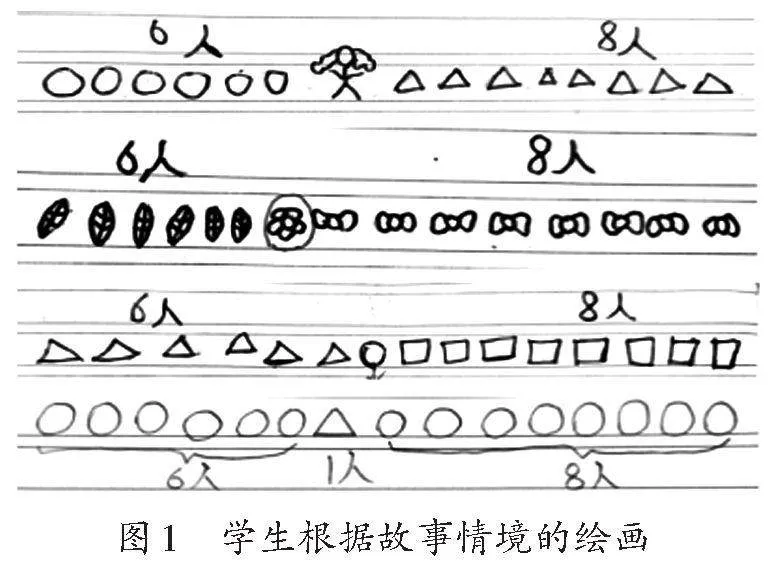
教师组织学生画一画“迷糊妹妹及小伙伴们排队练习舞蹈”的故事情节，引导学生把“排队问题”情境从形象过渡到抽象。学生用多种图形符号表示（如图1）。

4.故事为辅，建构模型

与传统的被动机械接受“填鸭式”教学模式相比，建构数学模型的过程可以鼓励学生积极参与课堂实验探究，促进学生的学习主动性和积极性，使得学生掌握的概念和知识更加全面、系统，从而提高学生学习效率。

学生通过用图形符号画出排队情境画面后，教师引导学生总结，以中间的人为参照，“排队问题”常见数量关系为：前面的人数+后面的人数u/9oweCUYWGWhCjdqj6BKA==+1=排队总人数（前+后+1=总人数），或前面的人数+1+后面的人数=排队的总人数（前+1+后=总人数）。建构了“排队问题”的核心基础模型，然后构建问题链，让知识形成网状结构，演变出其他模型，可最大限度地整合丰富多彩的问题。教师组织学生根据“迷糊妹妹从前面数排第7，从后面数排第9”进行探究，把故事情节演一演，形象展示用7+9计算后，排在中间的迷糊妹妹数重复了，全班交流并总结出数量关系式：从前往后数的序号+从后往前数的序号-1=排队的总人数（前序号+后序号-1=总人数）。

播放另一段数学微故事，马小飞用问题“迷糊妹妹从前往后数排第7，后面还有8人，一共有多少人？”考迷糊兄弟。学生观看视频后，教师放手让学生自主解决，学生通过画图表征，列式计算，构建出数量关系式：从前往后数的序号+后面的人数=排队的总人数（前序号+后=总人数）。继续播放数学微故事，迷糊兄弟求得总人数，把桃子分给妹妹及小伙伴后，她们跳了一支舞感谢迷糊兄弟，引导学生在接受别人的馈赠或帮助后，要表达谢意，从而渗透感恩德育思想。

5.故事为助，模型“曲成”

建立数学模型后，还要及时进行检验、运用，才算真正完成。教师组织学生尝试创编“排队问题”故事并解决，全班交流。其中3类“排队问题”故事比较有代表性。

（1）国庆节，笑笑和淘气去游乐园玩，他们排队玩彩虹滑道。工作人员说再玩15人就关闭滑道了，此时，从前面数笑笑排第9，从后面数笑笑排第7，淘气排在最后面，淘气能玩彩虹滑道吗？数量关系式：从前往后数的序号+从后往前数的序号-1=排队的总人数（前序号+后序号-1=总人数），列式计算，队伍共有9+7-1=15（人），淘气排最后，是第15人，能玩彩虹滑道。

（2）星期天早上，小丽和妈妈一起整理书架，小丽问这一层共有多少本书？妈妈说：“《故事大王》的左边有10本书，右边有8本书。”小丽说有这一层有18本书，你认为她说对了吗？数量关系式：前面的人数+后面的人数+1=排队的总人数（前+后+1=总人数），列式计算，一共有10+8+1=19（本），小丽说的不对。

（3）马小飞和文文去参观“动物之家”，猫咪洞在最顶层，从下往上数狗狗窝排第5层，狗狗窝上面还有3层，猫咪洞是从下往上数第几层楼？数量关系式：从前往后数的序号+后面的人数=排队的总人数（前序号+后=总人数），列式计算，总共有5+3=8（层），猫咪洞是从下往上数第8层楼。

学生通过创编“排队问题”故事并解决问题，能够更好地理解“排队问题”的数量关系，真正掌握解决“排队问题”的数学模型，从而灵活解决现实生活中的“排队问题”。

故事比理论更吸引学生的注意，生活中处处有故事，教学上，应用数学微故事辅助数学模型建构，创设现实情境，激发学生探索、建构数学模型的学习兴趣，帮助学生经历类似于数学家建模的再创造过程，并利用数学模型解决现实生活中的问题，从而培养学生的数学学习情感、提高学生数学学习质量。

［ 参 考 文 献 ］

[1] 王永春.小学数学与数学思想方法［M］.上海：华东师范大学出版社，2014.

［2］ 大卫·苏泽.教育与脑神经科学［M］.方彤，黄欢，王东杰，译.上海：华东师范大学出版社，2014.

［3］ 中华人民共和国教育部.义务教育数学课程标准（2022年版）［S］.北京：北京师范大学出版社，2022.