数感：数与运算一致性的认知基础

［摘 要］对数与运算一致性的认识和理解是学生学好数学的基本保障。文章以2024年版教材一年级上册为例，论述数感、数与运算一致性之间的联系，并通过解读新教材，阐释如何以现实情境为基础，以解决问题为主线，加强数感的培育，让教师、学生更容易认识和理解数与运算的本质，明确数与运算的一致性。

［关键词］数与运算一致性；数感；数数

［中图分类号］ G623.5 ［文献标识码］ A ［文章编号］ 1007-9068（2024）23-0009-03

数感是学生数学素养的重要组成部分，而理解数与运算的一致性则是建立数学逻辑框架的关键。在探讨数感培养及数与运算一致性的认识过程中，教师不仅需要深入研究和探讨教学策略，更要引导学生在课堂学习中切实地感受和领悟数的特征和运算的本质。下面以2024年版教材一年级上册为例，谈谈关于数感、数与运算一致性的教学思考。

一、数感和数与运算一致性

对数与运算的理性认识必须建立在坚实的数学基础和逻辑推理之上。这包括对数的基本概念、性质、运算规则及它们之间的关系有深入的理解。但在数学学习的启蒙阶段，如何运用现实情境和直观感知，让学生认识和理解数与运算的一致性呢？

（一）数感是理解数与运算一致性的认知基础

所谓数感，主要是指对数与数量、数量关系及运算结果的直观感悟，并能运用数描述和解决问题的意识与习惯。从认识论的角度来看，直观感悟在对数与运算的理性认识中扮演着重要的角色。它不是一种表面的、浅显的感觉，而是一种深入的理解与体验，是对数与运算的内在规律和逻辑关系的现实与抽象模型的直接把握。因此，在数学学习中，学生对事物的个数、次序、分布状态及关系的理解，都必须建立在对现实情境及其基本的数理逻辑关系的充分把握之上。在面对数与运算的问题时，这种直观感悟能够帮助学生迅速捕捉问题的本质。例如，在理解0、1、10的产生时，学生可以通过对度量离散量（如数鸡蛋个数）和度量连续量（如数尺子上的0、1、2等刻度）的直接体验，自然地理解0、1和10的本质，无须经过复杂的逻辑推理或证明。

（二）数与运算一致性是发展数感的有力支撑

理解和把握数与运算一致性对后续认识数有很大帮助。

首先，基于自然数基本单位“1”的数数规则，就会对9，10，11，99，100，101，999，1000，1001等的产生和使用有正确的认知。同时，“比1个多很多的东西‘捆着数’”“不够1个的东西‘切开数’”的直觉，对于学生认识分数、小数及正负数等都有着积极意义。

其次，在计数过程中确立了自然数“1”的基本单位后，会对10个“一”是“十”、10个“十”是“百”的计数单位制的规则有正确的认识，特别是对学习分数和小数的产生起到了正确的引导作用。例如，分数是在“一个东西分给两个人”的时候产生的，而小数是在“一个东西要分给十个人”的时候产生的。这种直觉能帮助学生理解计数结果小于“1”时，“零点几”是“几分之一”的另一种表达方式，从而避免了关于分数和小数的产生及其单位应用的许多认识误区，即小数是分数的另一种表达方式，小数的计数单位是分数的计数单位中的一类。

最后，沟通数与运算的本质联系。例如，加法是数的累加，是对“几堆事物”进行“从头数”“接着数”和“分段数”的累加过程和结果的呈现。进一步看，通过倒着数、等量数等方式解读减法、乘法和除法，都是在对数的运算中确定了“按几个数”的标准以后，对“单位个数”不同数法的数学表达。

总之，数感的形成对于把握数与运算一致性具有不可估量的意义。反过来，当把握了数与运算一致性后，就能摆脱文本阅读的限制，从而建立起真正的数学理解与数学思维。

二、教材示例与教学解读

《义务教育数学课程标准（2022年版）》中提到，数感表现为以下几个方面：能够在真实的情境中理解数的意义；能够用数表示物体的个数或事物的顺序；能够在简单的真实情境中进行合理估算，做出合理判断；能够初步体会事物背后简单的规律，用数表达这样的规律。这些内容为教学提供了方向，即如何渗透数与运算一致性。新修订的教材在这方面有显著的强调。

（一）建立以自然数“1”为基础的计数规则

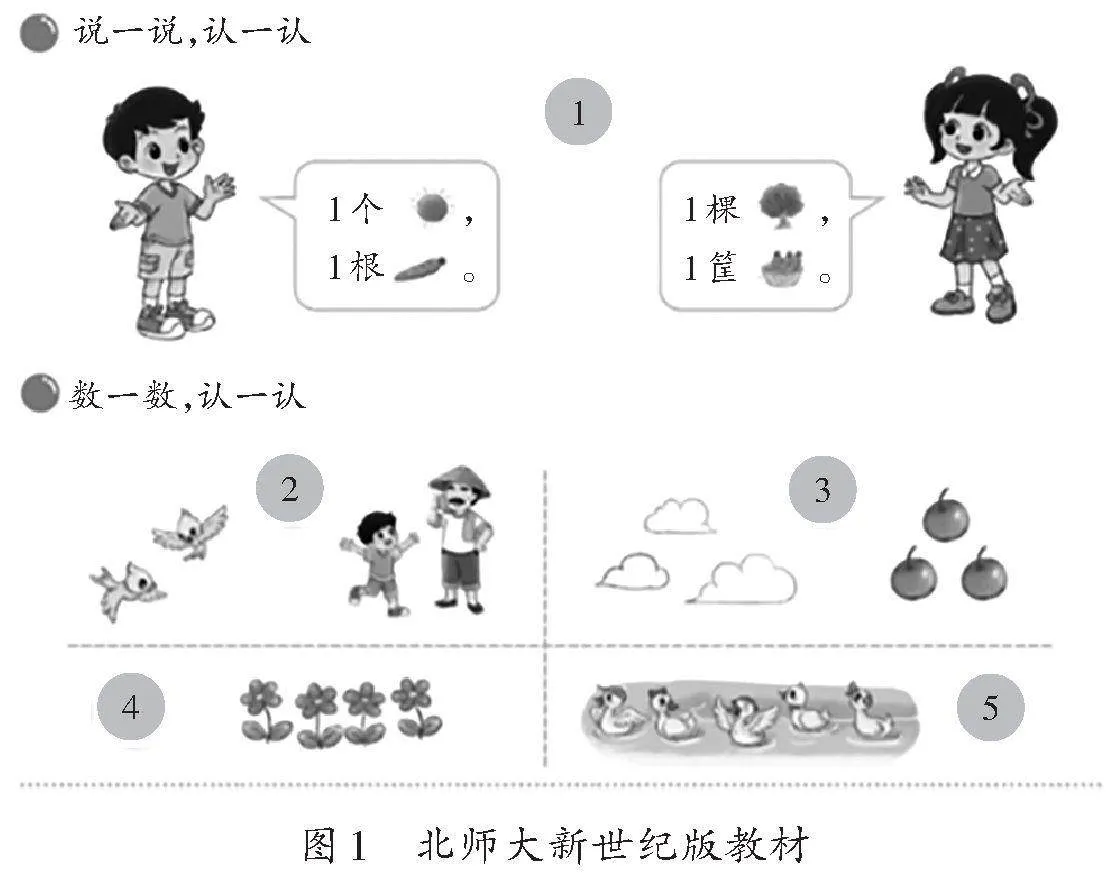
北师大新世纪版教材一年级上册第二单元“生活中的数”第12页“走进美丽乡村”（如图1）的内容是“5以内数的认识”：以“说一说”“数一数”“认一认”的活动突出“1”的作用。

与旧教材不同的是，第一幅图采用“1个”“1根”“1棵”“1筐”来描述各种事物的数量，让学生注意到前三个“1”都是指单个事物，而第四个“1”则不同，因为蔬菜被装在1个筐里，所以按“筐”来计数。这里隐含了一个计数规则，即单个元素与组合元素都可以用“1”来表示，但两者标准不同。这为学生将来认识几个、几筐、半个、半筐等数和量奠定了基础。

（二）用“接着数”和“连续数”建构加法模型

西南大学版教材一年级上册第二单元“0～9的加法”第30页“一共有多少条船？”（如图2）的内容是“加法”：有“把3条船和2条船合起来”的提示语，并把3个○和2个○圈起来。这和以前教材的内容差不多，但3名学生的对话揭示了加法的计算过程，即“从3条往后数2条”“从2条往后数3条”都是“接着数”，数到“5”。

同样，北师大新世纪版教材一年级上册第二单元“5以内的加与减”第29页“一共有多少”（如图3）呈现两只手里的笔“分开”与“合并”的情境图后，增加了“一只手里有3支粉笔，另一只手里有……”和“1，2，3，4，5，共有……”的对话框，以此提示学生“在分开数算不出总数时，就应该合起来从1开始一个一个地数”，然后利用“数熊猫”的情境图展示“接着数”的方法。

这两个例子充分运用了学生已有的“认数”“数数”和“写数”的经验，将幼儿园阶段常见的“3+2=5”这一基础数学知识具体化，让学生通过亲身体验来理解“几部分或几个数合起来的数更多一些”“加法就是一次性数数不能得到总数而需要从头数或者接着数”的概念，感悟到数学中的加法本质就是接着数。通过打通“数是数出来的”和“加法也是数出来的”之间的联系，学生能够真切地感受到数与运算一致性。这为学生后续学习减法（倒着数）、乘法（同数累加）和除法（同数等分）奠定了坚实的基础。

（三）用“分段数”打通多位数计算的算理和算法的联系

在进行多位数四则运算，特别是涉及进退位的计算时，传统的教学方法往往依赖死记硬背的计算法则，这种方法缺乏对算理的深入理解，导致学生只能机械地模仿。现在，通过运用数与运算一致性的认知，强调“数是数出来的”和“计算就是继续数”，可以帮助学生更好地理解算理。对于小的数，学生可以通过“接着数”或“从头数”来完成计算。而对于较大的数，则采用化繁为简的思想，通过“分段”“分层”“分级”的方式，按照计数单位之间的换算关系继续数。

西南大学版教材一年级上册第五单元第89页“进位加法”的“一共有多少瓶水”（如图4）：让学生首先感觉到图中是“盒子里有9瓶，地上有2瓶，手上有1瓶”，但算式和图示表达的都是“9瓶加3瓶”的意思。图中的小棒图和计数器图会让一些学生觉得复杂，然后产生畏难情绪。对此，教师应该引导学生利用“9，1，2”这三个提示性数字，仔细观察图示中的操作。通过仔细观察和思考，学生会发现图示中的操作都是“将两段数数分解为三段数数”，即从“3”中分出一个“1”，那么从9往后数一个数就是10，再接着往后数两个数“11”“12”，这样就完成了计算。

这样，学生在学习西南大学版教材三年级下册第二单元第27页“两三位数除以一位数”的“分月饼”（如图5）时，就能在除法中通过数与分，把整十数、整百数进行“分段数”和“把大单位换算成小单位”，从而完成比较复杂的计算和说理了。

新修订的数学教材站在核心素养培育的高度进行修订与设计，以现实情境为基础，以解决问题为主线，加强了数感的培育，让教师、学生更容易认识和理解数与运算的本质，明确数与运算一致性，为学生将来解决更复杂的数学问题打下了坚实的基础。

［ 参 考 文 献 ］

[1] 郑大明.“数学眼光”的基本表现及其评价：基于数感、量感、形感的思考[J].小学教学参考.2021（29）：3-6.