揭“费马点”面纱 探模型间联系

刘焕 邢成云

【摘  要】  几何最值问题种类多、变换形式多样，是近几年全国中考比较热的模型考点.中考题目涉及的线段最值模型中，含有“将军饮马、阿氏圆、胡不归、费马点”等不同类型.通过“费马点”模型的由来追溯与其基本模型、重要结论的呈现与证明，探寻不同题目中不同模型之间的内在联系.

【关键词】  费马点；旋转变换；最小值；数学模型

1  “费马点”模型的由来

1643年，在一封写给意大利数学家和物理学家托里拆利（Evangelista Torricelli）的私人信件中，费马提出了下面这个极富挑战性和趣味性的几何难题，请求托里拆利帮忙解答：给定不在一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最短的点的位置.后来人们就把平面上到一个三角形的三个顶点A，B，C距离之和最小的点称为△ABC的费马—托里拆利点（Fermat-Torricelli point），也简称为费马点（Fermat point）或托里拆利点（Torricelli point）.

2  “费马点”基本模型

以△ABC的三边向外分别作等边三角形（如图1），然后把外面的三个顶点与原三角形的相对顶点分别相连，交于点P，则点P是△ABC的费马点（方便起见如简图2）.

图1

图2

2.1  定义：费马点就是到三角形的三个顶点的距离之和最小的点［1］.

2.2  费马点结论

（1）当三角形的最大内角小于120°时，费马点是对各边的张角都是120°的点；

（2）当三角形的最大内角大于等于120°时，费马点与最大角顶点重合［1］.

2.3  费马点的证明

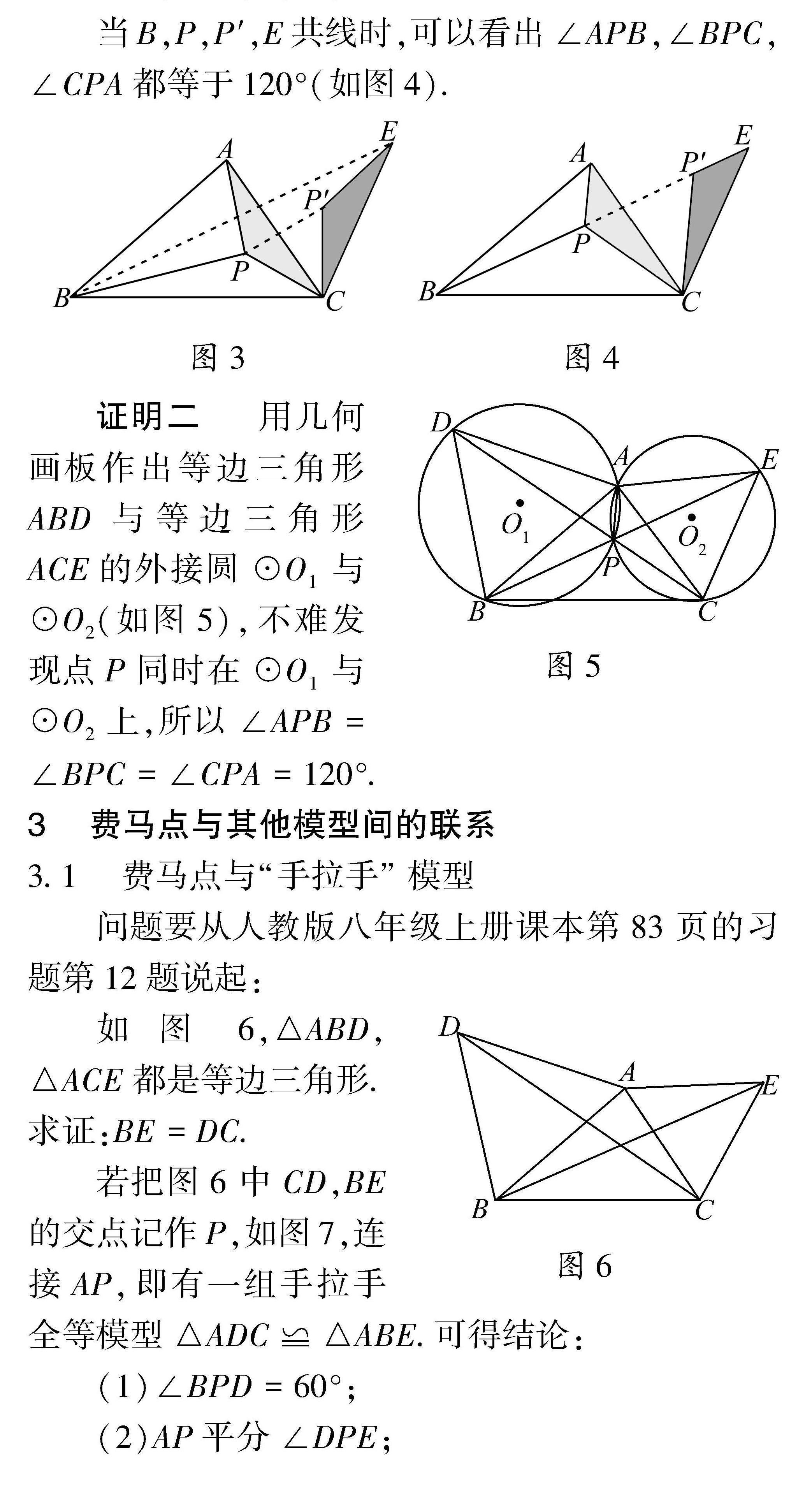
证明一  将图2中的△APC绕点C顺时针旋转60°得到△CP′E，如图3，则AP=EP′，△CPP′为等边三角形，则CP=PP′，PA+PB+PC=P′E+PB+PP′最小，即B，P，P′，E共线.

当B，P，P′，E共线时，可以看出∠APB，∠BPC，∠CPA都等于120°（如图4）.

图3          图4

图5

证明二  用几何画板作出等边三角形ABD与等边三角形ACE的外接圆⊙O1与⊙O2（如图5），不难发现点P同时在⊙O1与⊙O2上，所以∠APB=∠BPC=∠CPA=120°.

3  费马点与其他模型间的联系

3.1  费马点与“手拉手”模型

问题要从人教版八年级上册课本第83页的习题第12题说起：

图6

如图6，△ABD，△ACE都是等边三角形.求证：BE=DC.

若把图6中CD，BE的交点记作P，如图7，连接AP，即有一组手拉手全等模型△ADC≌△ABE.可得结论：

（1）∠BPD=60°；

（2）AP平分∠DPE；

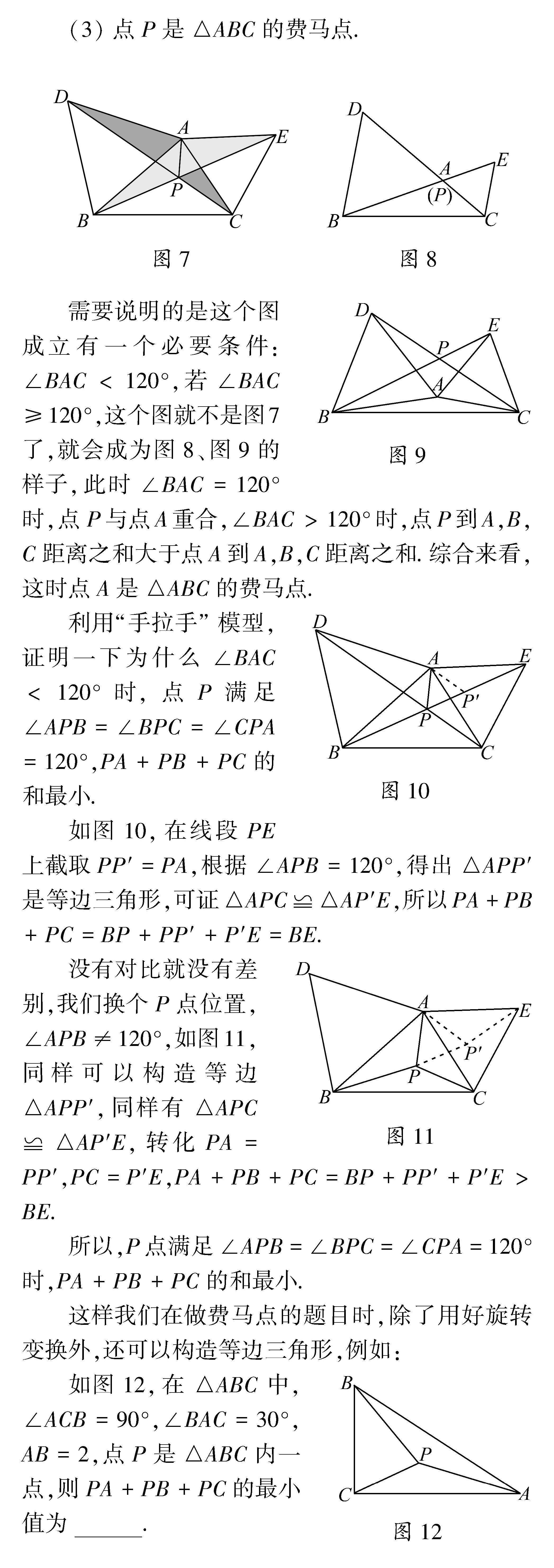
（3）点P是△ABC的费马点.

图7

图8

图9

需要说明的是这个图成立有一个必要条件：∠BAC<120°，若∠BAC≥120°，这个图就不是图7了，就会成为图8、图9的样子，此时∠BAC=120°时，点P与点A重合，∠BAC＞120°时，点P到A，B，C距离之和大于点A到A，B，C距离之和.综合来看，这时点A是△ABC的费马点.

图10

利用“手拉手”模型，证明一下为什么∠BAC<120°时，点P满足∠APB=∠BPC=∠CPA=120°，PA+PB+PC的和最小.

如图10，在线段PE上截取PP′=PA，根据∠APB=120°，得出△APP′是等边三角形，可证△APC≌△AP′E，所以PA+PB+PC=BP+PP′+P′E=BE.

图11

没有对比就没有差别，我们换个P点位置，∠APB≠120°，如图11，同样可以构造等边△APP′，同样有△APC≌△AP′E，转化PA=PP′，PC=P′E，PA+PB+PC=BP+PP′+P′E＞BE.

所以，P点满足∠APB=∠BPC=∠CPA=120°时，PA+PB+PC的和最小.

这样我们在做费马点的题目时，除了用好旋转变换外，还可以构造等边三角形，例如：

图12如图12，在△ABC中，∠ACB=90°，∠BAC=30°，AB=2，点P是△ABC内一点，则PA+PB+PC的最小值为    ．

这道题是2021年滨州数学中考第18题，可以从旋转和构造等边三角形两种方法来进行求解.

方法一  将△APB绕点A顺时针旋转60°得到△ADE，如图13，连接PD，CE，当点C，P，D，E共线时，PA+PB+PC=CE时值最小.

图13

图14

方法二  以AB为边作等边△ABE，连接CE，如图14，根据上面的“手拉手”模型我们可以知道，当PA+PB+PC=CE时值最小.这道题也可以以BC为边作等边三角形，因为∠BAC=30°，所以以AB为边作等边三角形便于计算.

费马点问题的解题思路是构造60°的旋转，如果了解费马点，可直接进行处理，如方法二，这时P点的位置就不重要了.但这个方法二也有取巧之嫌，可快捷解决选择题和填空题.

除了滨州中考题，近两年在其他地市中考题中也有涉猎，如2022年四川宜宾市第12题，2021年辽宁丹东市第16题，2020年重庆市A卷第26题，2023年湖北随州市第23题等.尤其是2023年湖北随州第23的第（3）问，以阅读理解的形式考查了学生即学即用的数学素养，它不但考查了费马点的数学意义，还体现了费马点在实际问题中的应用，是一道价值不菲的好题目，限于篇幅，仅展示一下第三小问.

图15

如图15，设村庄A，B，C的连线构成一个三角形，且已知AC=4km，BC=23km，∠ACB=60°.现欲建一中转站P沿直线向A，B，C三个村庄铺设电缆，已知由中转站P到村庄A，B，C的铺设成本分别为a元/km，a元/km，2a元/km，选取合适的P的位置，可以使总的铺设成本最低为    元．（结果用含a的式子表示）

3.2  费马点与“胡不归”模型

“胡不归”问题常以动点问题为背景，典型的利用等效法，与三角函数、相似等知识结合来解决.以下即为用“胡不归”模型解决费马点问题的例子.

如图16，在△ABC中，AC=2，BC=2，∠BCA=15°，在△ABC的内部有一点P，连接PA，PB，PC，则PA+PB+3PC的最小值为    .  图16

PA+PB+3PC不符合“胡不归”问题的kAP+BP（0

图17

像上题所求最值中三条线段的系数有不为1的情况，被称之为“加权费马点”问题［2］，

图18

解决方法还可以通过旋转进行线段转化，只不过要根据系数的情况选择不同的旋转或放缩方法（在此不再展示）.

另，如图18，在等边三角形ABC中，边长为4，P为△ABC内部一点，求AP+BP+2PC的最小值.

说明  这个题出现了2PC，可以以PC为斜边，构建等腰直角三角形（如图19），也可以以PC为直角边，构建等腰直角三角形（如图20），进而把问题化解.

图19

图20

3.3  费马点与“将军饮马”模型

“费马点”问题与“将军饮马”问题有着异曲同工之妙，都是求线段和的最小值，只是“将军饮马”是通过轴对称变换结合“两点之间，线段最短”及“垂线段最短”等数学基本事实来解决；而“费马点”模型其精髓所在则是通过旋转来改变线段的位置，优化图形的结构（要么集中分散条件、要么化隐为显、要么化不规则为规则），再结合“两点之间，线段最短”及“垂线段最短”等数学基本事实来解决［3］.其实，轴对称变换与旋转变换是内在相通的，限于篇幅，不再赘述.

4  几点思考

4.1  用好几何模型，提升数学能力，发展核心素养

初中几何被归纳出来的几大模型，其实原型都在教材当中［4］.如前文提到的人教版八年级上册课本第83页的12题，本身潜藏着好几个重要模型，外显的“手拉手”旋转模型，内蕴的角平分线模型和“费马点”模型，以此题为基，不断改编和拓展，可衍生出诸多中考题，成为命题专家命题的重要题根.模型思想属于一类可靠且被验证为有效的数学思想，教师在开展教学活动的过程中，利用各种各样的几何模型能有效缩短认知的长度，降低学生理解的难度.围绕这些模型的学习，可以不断培养和发掘学生的空间感知力、想象力，让学生能快速建立空间思维，有效提高学生对于几何知识的理解和把握，扩展几何眼光，不仅能使学生提质增智，还能更好地发展学生的核心素养.

4.2  几何模型教学，破除循规蹈矩，依循自然合理

作为教师由于先得先知，具有丰富的解题经验，容易将几何模型高度提纯而一步到位，存在不自觉的惯性思维，而缺少对学生解决问题必要的过程指导，导致学生短时间内难于理解接受.如前文提到的人教版八年级上册课本第83页的12题，在学生刚开始学习时，切忌直接告知学生这是“手拉手模型”以及隐含的费马点模型，而是需要学生在后续的练习、作业以及测试中反复感知这类模型，通过类比、分析，归纳等一系列数学思维活动过程再引出来，会让学生认识更深刻，更容易理解接受，从而内化为学生的认知.如果一开始就直接告知、讲解这些模型，如同天降结论，会使学生对横空出世的模型结构认识不足，理解自然浅薄，在应用时往往就只能照猫画虎、生搬硬套.一旦外显条件不具备，或者问题进行了乔装打扮，就难以迁移而不得思路.因为学生在没有对模型结构通透之前，获得的是惰性知识，没有活力，只能硬套模型，惯性而为.从而导致学生反复的学模型，老师反复的教模型.所以说，在教学时要把握好度，要破除循规蹈矩、亦步亦趋，一味地套用模型练习，而是要教好“专家思维”，引导学生学会思考如何将模型巩固好、迁移好.

4.3  立足教材基地，加强培根固原，探寻模型关联

当下有一个不好的倾向，重教辅，轻教材，把教辅上盛行的模型奉为圭臬，其实教材上的每一个概念、定理（公理）、性质，包括教材上的典型例题均是一个模型.“费马点”给人高大上的感觉，前文的分析我们已经清楚，其模型就在教材中，而不是从天而降的飘来物.所以说，我们不能死守模型，唯模型是举，若不能融会贯通之，就会落入模型的窠臼而固化自己的思维.基于此，作为教师要深耕教材，把最基本的、最重要的基本图形帮助学生加固好，并善于挖掘教材本体中内隐的思想方法，使之成为处理问题的利器，通过数学的思想观念去统领所谓的什么模型.另外，几何模型间不是相互独立的，模型的教学也并不仅仅是教会学生解决单一的问题，旨在培养学生抽取模型的能力和应用模型的能力［4］.通过探寻各类模型之间的关联，把模型进一步结构化，成为更上位的统帅，如此，才能真正地落实好减负增效，若在中考复习阶段纠缠于这些模型，往往适得其反，加重了学生的负担不说，还会阻碍学生关键能力的提升.

参考文献

［1］郭金花.费马点问题与构造旋转拉直法［J］.中小学数学（初中），2021（06）：32-33.

［2］刘霞.与“费马点”相关问题的处理策略［J］.初中数学教与学，2019（10）：28-31.

［3］杨世奇.初中几何最值问题的数学史模型［J］.初中数学教与学，2021（10）：32-34.

［4］章蓓蓓，朱雅莉.用好几何模型，提升数学能力［J］.林区教学，2023（01）：71-75.

作者简介

刘焕（1986—），女，山东滨州人，中学二级教师，多次执教市观摩课，曾获山东省教学成果一等奖；主要从事课堂教学及中考研究.

邢成云（1968—），男，山东滨州人，中学正高级教师（二级）；教育部名师领航工程邢成云名师工作室主持人，国家“万人计划”教学名师，山东省突贡专家，山东省特级教师，齐鲁名师；主要研究初中数学课堂教学及中考研究，发表论文200多篇，其中20篇被中国人大书报资料复印中心全文转载.