基于建构主义学习理论、指向应用意识培养的数学史融入初中课堂的教学探讨

贺鑫 梁海华

【摘  要】  应用意识是义务教育数学新课标所提出的核心素养之一.以相似三角形为例，探讨基于建构主义学习理论的数学史融入应用课的教学方法.通过创设数学情境，设计探究活动等手段，引导学生经历观察分析、自主探索、合作交流、猜想计算等过程，自主建立相似三角形的数学模型，达到促进学生把握数学本质、自主构建知识、培养应用意识的目的.

【关键词】  数学史；建构主义学习理论；应用意识；相似三角形

《义务教育数学课程标准（2022年版）》将培养应用意识作为课程目标之一，强调需有意识地利用数学的概念、原理和方法解释现实世界中的现象与规律，解决现实世界中的问题［1］.数学史具有深厚的文化底蕴，记录了数学在不同历史时期和文化中的应用和发展.它不仅仅是关于数学知识的历史，还反映了数学家在解决问题时的思维方式和思想方法，帮助人们了解在古代和近现代社会中，数学家们如何解决现实世界中的各种问题，从而激发学生的应用意识.通过数学史融入教学，了解数学家们如何思考问题、建立模型、提出假设和验证从而解决问题，一方面能使学生更好地理解如何将数学方法应用于实际问题，另一方面通过建立数学与现实生活、与其他学科的联系，有助于培养学生养成理论联系实际的习惯，发展实践应用能力.国内许多数学教育研究工作者在这方面开展了一系列的探索，取得了丰富的研究成果，参见文［2-4］等文献.建构主义学习理论的核心理念是引导学生主动构建自身的知识体系，它与数学史融入数学的教学以帮助学生自发构建和形成数学概念、定理有着相融相促的作用.但据笔者所知，目前国内外结合建构主义学习理论来开展数学史融入几何课堂教学的研究工作并不多见.因此，本文将以建构主义学习理论为指导，选取人教版九年级下册“相似三角形的应用举例”一课，从应用课出发，以学生生活经验为背景，融入数学史展开教学，让学生在感悟数学知识抽象和发展的过程中，构建模型观念，培养应用意识.

1  建构主义学习理论

由瑞士著名心理学家皮亚杰和美国教育家布鲁纳等人提出的建构主义学习理论，认为学生本身具备主动学习和处理信息的能力，教育者的任务是提供适当的教育环境和机会，以激发学生的学习兴趣并引导学生主动构建自己的知识体系.该理论主要有如下几个观点.（1）知识观

建构主义强调知识的动态性，其提出知识并不是问题的最终答案，是在人类进步的过程中，不断改正并出现的新的假设和解释.在建构主义学习理论的知识观中认为知识需要针对具体情境再创造，学习者会基于自己的经验背景进行理解并建构属于自己的知识.

（2）学习观

建构主义在学习观上强调学习的主动建构性、社会互动性和情境性三方面.建构主义学习理论认为知识是不可能脱离活动情境而孤立存在的，学习是在一定的社会文化情境下，通过人际间的协作活动而实现的意义建构过程，因此“情境”“协作”“会话”“意义建构”是学习环境中的四大要素或四大属性［5］.（3）学生观

建构主义学习理论强调关注学习者本身已有的知识经验结构，认为学习者应该处于主体地位，在学习新信息、解决新问题时都需建立在已有的知识经验上.因此，在实际教学中，教师需将新知识建立在学生已有的知识经验上，引导学生生长出新的知识经验，完善认知结构.（4）教师观

建构主义认为教师是学生知识建构过程的帮助者、引导者、合作者.教学不是教师简单的转移和传递知识，而是教师在师生共同的活动中，为学生理解提供阶梯，帮助学生形成分析、解决问题的思路，创造良好的、富有挑战性的学习情境，引导学生“正确构建”“高效构建”.

建构主义学习理论强调教学是在学习者本身的内在知识结构上，帮助他们将外部的客观事物内化成其内在的知识结构.其指出学习者应处于主体地位，即教学是促使学习者成为主动、积极的知识建构者，逐渐建构自身的知识结构［6］.因此，教师应在教学中创造符合学生知识经验的课堂情境，让学生自主建构知识体系.而数学史知识的融入能帮助教师根据历史情境及数学家的思想方法更好地建立课堂情境，提升学生学习数学、解决问题的内驱力.

2  教学设计与实施

2.1  设计理念

根据建构主义的基本观点，教师需从学生已有的知识经验出发，设计丰富的情境，开展教学设计和活动.故本节课首先通过复习相似三角形的判定定理与性质，为学生解决问题提供知识基础.再设置3个历史情境，激发学生的主观能动性.情境1：结合教材上泰勒斯测金字塔高度问题，丰富其历史背景引导学生分析探究；情境2：以教材所呈现的测河流宽度问题为基础，结合历史故事设计问题，进行重构；情境3：以《九章算术》中的勾股容方内容创建问题情境.通过情境问题的提出、探究过程，促使学生理解和掌握基础知识和基本技能，培养深度探究的思想与能力，提炼建立相似三角形模型的核心方法，促使学生逐步形成核心素养.

2.2  教学过程

2.2.1  复习旧知，奠定基础

教师提问：判定两个三角形相似有哪些方法？相似三角形有哪些性质？

出示操作题

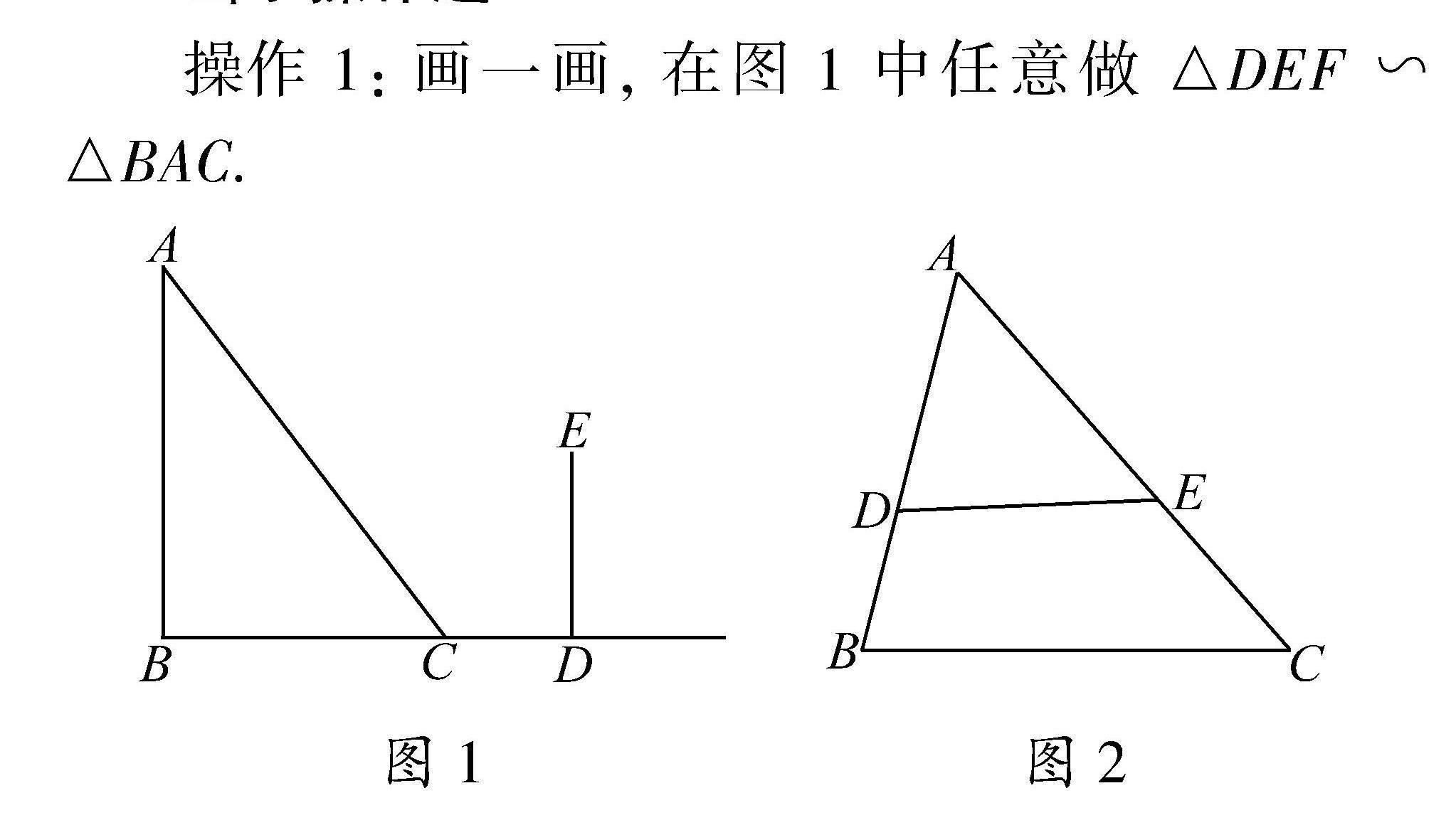
操作1：画一画，在图1中任意做△DEF∽△BAC.

操作2：如图2，在△ABC中，点D、点E分别在边AB，AC上，请你添加一个条件，使△ABC∽△ADE，并说明理由.

2.2.2  模型初建，思维发散

情境1  泰勒斯测金字塔高度

教师播放视频——神秘的金字塔：介绍泰勒斯及其利用木杆测出金字塔高度的故事.提问：泰勒斯仅利用一根木杆就测出金字塔的高度，他是如何做到的呢？

学生1：太阳是平行光线，照射在金字塔上会形成影子，在某个地方放一个木杆，也会形成影子，同一时刻物体和影子的高度比是一样的，所以只要测出金字塔的影子长度、木杆高度以及影长，利用相似比就可以求出金字塔的高度.

教师：非常棒，这就是聪明的泰勒斯的做法，借助平行光线与金字塔以及木杆所成的夹角相等，从而构建相似三角形，借助对应边成比例，即可求出金字塔的高度.随即播放视频：完整讲解泰勒斯的做法，以多媒体展示求解过程.

解：如图3，因为太阳光是平行光线，

所以∠ABO=∠EDF.

因为∠AOB=∠DFE=90°，

所以△BAO∽△DEF.

因为相似三角形对应边成比例，

所以BOFD=OAEF，

所以BO=OA·FDEF=201×23=134m.图3

教师追问：是否还有其他的模型构建方式？

学生2：将木杆立在金字塔的影子的中间，使得木杆的影子顶端与金字塔的影子顶端重合，也可以构建相似三角形.（学生上台画图展示，如图4）

教师：非常好，其实我们这两种方法的原理都是通过太阳光线构建相似三角形模型，通过对应边成比例求未知边的长，只是构建方法不一样.

2.2.3  改变模型，解决问题

情境2  拿破仑测河宽

教师：拿破仑·波拿巴（1769—1821），19世纪法国伟大的军事家、政治家，法兰西第一帝国的缔造者.1805年，法国拿破仑与德军在莱茵河畔激战，如图5所示，拿破仑位于莱茵河南岸A处，德军在莱茵河北岸B处，因不知道河宽，法军大炮很难瞄准敌兵营.假设AB垂直于河流，你能利用相似三角形的相关知识帮助拿破仑解决问题吗？

学生3：连接AB，交河流边界于点D，从点A作合适长度的线段AC平行于河流边界，再连接BC，交河流边界于点E，可以得出△BDE∽△BAC，只要测出AC，AD，DE的长度就可以求出AB的长度了.（上台展示画图，如图6所示）

教师：很好，大家已经可以从依据已有的外部条件构造相似三角形提升到自己创造条件来构造相似三角形解决问题了.若DA=45m，AC=90m，DE=60m，请你根据这些数据计算AB间的距离.

学生4：

解：因为DE∥AC，

所以△BDE∽△BAC，

所以BDBA=DEAC，

即BA-ADBA=DEAC，BA-45BA=6090，

BA×60=（BA-45）×90，

解得BA=135.

因此，BA间的距离为135m.

2.2.4  形式多变，变式探究

情境3  勾股容方问题

教师提问：汉代数学名著《九章算术》勾股章中设题：“今有勾五步，股十二步，问勾中容方几何.”答曰三步十七分步之九.术曰：“并勾、股为法，勾股相乘为实，实如法而一，得方一步．”你知道这是怎么求出来的吗？请同学们画出图象，尝试解决［7］.

分析问题：现有一直角三角形，勾（短直角边）长为5，股（长直角边）长为12，问该直角三角形能容纳的正方形边长最大是多少？

教师提问：如果在Rt△ABC中要做一个最大的正方形，你有几种做法？学生小组讨论，合作探究，展示两种不同做法，计算正方形边长，进行对比.

学生5：以两条直角边做正方形的边长，可作出图7所示的正方形DBFE，利用△ADE与△ABC相似即可求出正方形边长.（上台板演证明过程）

解：因为∠A=∠A，∠ADE=∠B，图7

所以△ADE∽△ABC，

所以ADAB=DEBC.

设BD=DE=x，则AD=12-x，

所以12-x12=x5，

所以x=6017.

学生6：也可以以斜边中的一部分为正方形的边长.（用数学语言板书证明过程如下，如图8）

解：由题意与图形可知图8

△GBK∽△KOC∽△ABC，

所以GKAC=BKBC，OKAB=CKAC.

设GK=OK=x，

所以x13=BK5，x12=CK13，

所以BK=5x13，CK=13x12，

而BK+CK=BC=5，

所以5x13+13x12=5，

所以x=780229.

教师总结：通过计算可知6017＞780229，所以方法1的面积更大.现在同学们已经能够针对问题构建不同的相似三角形模型来解决问题了，这是非常大的进步.

2.2.5  总结要点，结构形成

教师：同学们，在刚刚的三个情境问题中，我们都是通过构建相似三角形来解决问题的，那能否总结相似三角形模型构建的步骤和要点呢？

师生共同梳理：

①梳理题意，将实际问题转化为数学问题，构建数学模型.

②寻找模型中能够证明三角形相似的条件，列出相似比求解.

③图形与几何的计算问题，需要先经过证明，再进行计算.

④将解决的数学问题还原为实际问题，还原中注意反思模型实践时可能存在的问题与解决办法［8］.

2.2.6  应用练习，加深理解

①测学校旗杆高度.

②测学校后方河流宽度.

3  结论与启示

著名数学家克莱因指出：“数学史是教学的指南.”本文以数学史为主线，以建构主义理论为指导，创设相关情境问题，引领学生站在前人的肩膀上，在生活中、在自然中发现数学，培养应用意识.笔者认为，在实施基于建构主义学习理论下的数学史融入中学课堂教学时，采用以下三个策略，将会收到良好的效果.

3.1  立足教材，挖掘历史背景创设情境

教材为学生的数学学习活动提供了主题、基本线索和知识结构，是实现数学课程目标、实施数学教学的重要资源.在教学中我们应深度解读教材，挖掘数学知识现实背景.随着新课改的逐渐推进，教材中不断融入更丰富的实际生活情境，更为生动地呈现数学知识，旨在突显数学知识的实际应用性，激发学生对数学应用的深刻认识，进一步体现其实用性与价值.本文以教材内容为基础，融入数学史，创设简明生动的生活情境，从现实生活中发现数学问题，把生活与知识联系起来，并运用知识解决生活中的数学问题，将学生为了“考试”而学习转变到因为“数学有用”而学习，才是培养应用意识的最终目的.

3.2  加强数学建模教学，提升应用意识

数学建模是数学与现实联系的基本途径，主要指通过建立数学模型来解决实际问题的过程［8］.本节课根据历史背景来引导学生构建相似三角形模型解决问题，让学生掌握前人构建的数学模型和其中蕴含的思想方法，使学生能更好地运用相关模型解决数学问题和实际问题.数学建模为学生提供了自主学习的空间，有助于体验数学在解决实际问题中的价值和作用.在教学中，教师要善于引导学生从生活实际中发现数学知识，更要引导学生将所学知识应用到实际生活中去，形成解决实际问题的有效策略，适应社会发展的需要，强化应用意识.

3.3  思维碰撞，自主迸发应用意识

数学课堂应是积极思考、思维碰撞的平台.教师在创造和谐轻松学习氛围的同时，应充分调动学生的主动性，促使他们积极主动地学习，使创造潜力能够以最大限度发挥.通过数学史的融入，让课堂上不止有师生之间、生生之间的思维碰撞，更激发了学生与伟大数学家之间的思维交流，促进学生创造性地解决问题，自主迸发应用意识.

参考文献

［1］

中华人民共和国教育部.义务教育数学课程标准：2022年版［M］.北京：北京师范大学出版社，2022.

［2］李明振，庞坤.数学史融入中学数学教材的原则方式与问题［J］.数学通报，2006（03）：23-25.

［3］曾峥，杨豫晖，李学良.数学史融入初中课堂的案例研究［J］.数学教育学报，2019，28（01）：12-18.

［4］汪晓勤.关于HPM课堂教学评价的案例分析［J］.数学通报，2021，60（10）：6.

［5］何克抗.建构主义──革新传统教学的理论基础：上［J］.电化教育研究，1997（03）：3-9.

［6］付茁.建构主义学习观对数学教学的启示［J］.教学与管理，2007（27）：68-69.

［7］余旭红.解决相似形问题的思想方法［J］.试题与研究，2018（28）：16-19.

［8］李新菊.HPM视角下渗透数学建模思想的教学设计：以“相似三角形的应用”为例［J］.数学教学通讯，2022（17）：26-28.

作者简介  贺鑫（1997—），女，硕士研究生；主要研究数学课程教学论；

梁海华（1979—），男，博士，教授，学校第六届教学名师;现为中国数学会奇异摄动专委会委员、广东省工业与应用数学学会常务理事;作为负责人承担了3项国家项目、3项省部级项目的研究工作，以第一或通讯作者在国内外权威期刊上发表数学学术研究论文40多篇，教学改革研究论文10篇；获得广东省自然科学奖二等奖，广东技术师范大学教学成果奖一等奖.