大型水运枢纽船舶闸室连续排挡模型及算法研究
陈登峰 李一博 汪磊 姚红云 杨俊毅
DOI:10.3976/j.issn.1002-4026.20230069
收稿日期:2023-04-20
基金项目:云南交投科研项目(YCIC-YF-2021-12);重庆市教育委员会青年项目(KJQN202100715);重庆交通大学研究生科研创新项目(2022S0035)
作者简介:陈登峰(1990—),男,博士研究生,工程师,研究方向为公路及水路运输。E-mail:1184361775@qq.com
*通信作者,李一博(1999—),男,硕士研究生,研究方向为公路及水路运输。Tel:19936080200, E-mail:LiybJacob@yeah.net
摘要:为提高内河通航设施船舶通航效率,提高通航设施工作能力,提出一种可以求解考虑船舶顺序入闸和不考虑船舶顺序入闸两种情况的船舶闸室连续排挡模型和算法。利用二维装箱问题模型建立船舶闸室连续排挡模型,采用贪婪策略思想,提出船舶闸室连续排挡模型求解算法。根据百色枢纽工程生成仿真到闸船舶船型数据,用算法进行闸室排挡计算。结果表明,在随机生成90艘船舶的情况下,考虑船舶到闸顺序的排挡结果需要使用47个闸次,闸次平均占用率为76.424%,不考虑船舶到闸顺序的排挡结果需要使用45个闸次,闸次平均占用率为76.821%,模型和算法能够对不同情况下船舶闸室进行有效连续排挡。
关键词:内河航运;船舶排挡;二维装箱;贪婪策略
中图分类号:U641.7 文献标志码:A 文章编号:1002-4026(2024)03-0121-10
开放科学(资源服务)标志码(OSID):
Continuous gear shifting model and algorithm of ship lock chambers
in a large water-transport hub
CHEN Dengfeng1,2,3,LI Yibo2*,WANG Lei3,YAO Hongyun2,YANG Junyi3
(1. Yunnan Highway Engineering Supervision and Consultancy Co., Ltd., Kunming 650021,China;
2. College of Traffic &Transportation,Chongqing Jiaotong University,Chongqing 400074,China;
3. Bose Hub General Aviation Investment Co., Ltd.,Baise 533000,China)
Abstract∶To enhance the navigation efficiency of ships in inland waterway navigation facilities and increase their operational capacity, a continuous gear shifting model and algorithm for ship lock chambers are proposed. This model comprises two scenarios: considering and not considering the sequence of ships entering the lock . First, a two-dimensional packing problem model was employed to establish a continuous gear shifting model for ship lock chambers. Then, an algorithm for solving the aforementioned continuous gear shifting model based on a greedy strategy was proposed. Finally, simulated ship data for vessels arriving at the lock was generated based on the Baise Junction Project. The proposed algorithm was used to calculate the lock chamber gear arrangement. Results indicate that, in the case of randomly generated data for 90 ships, 47 lock cycles were required for the gear arrangement considering the ship arrival sequence, with an average occupancy rate of 76.424%. However, only 45 locks were needed for the gear arrangement when the ship arrival sequence was not considered, with an average occupancy rate of 76.821%. The proposed model and algorithm can effectively shift gears continuously in the ship lock chamber under various conditions.
Key words∶inland water transport;ship gear shifting;two-dimensional packing; greedy strategy
在内河航运中,船舶一般利用通航设施克服水位落差,常见的通航设施包括船闸、升船机以及结合两种通航水工建筑物的“船闸+升船机”复合通航设施。通航设施的工作效率影响航道的畅通和高效,船舶在通过通航设施时,需要进入闸室,闸室的利用率和使用数量是影响通航设施工作效率的重要因素之一[1]。为优化内河水运枢纽通航设施通航效率,必须对船舶闸室分配问题进行分析,降低船舶在通航时的闸室使用数量,最大化闸室利用率。
船舶闸室排挡问题是一个复杂的组合优化问题,在国内外学者中得到了广泛的关注与研究。近年来,涉及船舶闸室分配的研究主要集中在传统算法、深度学习、多目标优化、模拟仿真等多个方面[2-4]。传统算法研究包括贪心算法、动态规划算法、遗传算法[5]等,这些算法通过对船舶的数量、尺寸、航行时间等因素进行考虑,制定出不同的闸室分配方案[6]。近年来,深度学习技术的发展为船舶闸室分配问题的研究带来了新的思路。利用神经网络等深度学习技术[7-10],可以从大量的历史数据中提取规律,从而制定出更为准确的闸室分配方案。目前船舶排挡方法大多针对单一闸室内的船舶排挡进行求解,由于闸室内可放置船舶较少,大量研究采用智能算法进行求解,浪费大量算力,且求解不稳定,不适用于工程应用。因此,本文提出一种可以应用于工程领域,进行连续求解的船舶闸室连续排挡模型。
本文首先利用二维装箱模型[11]建立船舶闸室连续排挡模型,随后采用贪婪策略分别建立考虑船舶到闸顺序的闸室排挡算法和不考虑船舶到闸顺序的闸室排挡算法[12]。最后,以百色枢纽工程为例,随机生成到闸船舶船型,对模型及算法进行验证。
1 船舶闸室连续排挡问题
船舶闸室分配问题是指在船舶通过通航设施时,通过调整船舶在闸室内摆放的位置,达到通航设施最优通航效率[13]。不合理的闸室分配会导致等待时间过长、航运效率低下等问题。在建立闸室连续排挡问题模型时,需要定义闸室信息和船舶信息。
将第n个闸室船舶信息定义为Bn,Bn=W,H,n,其中W和H表示闸室的宽度和长度,一般为固定数值。在船舶信息定义中,用ai表示第i艘船舶ai=hi,wi,i,其中hi和wi表示船舶包含安全距离在内的宽度和长度,船舶之间安全距离应根据相关规范标准确定,至少不小于船舶长度或宽度的20%,船舶申报到达的船型信息,根据优先规则排列后记为A=a1,a2,…,ai。
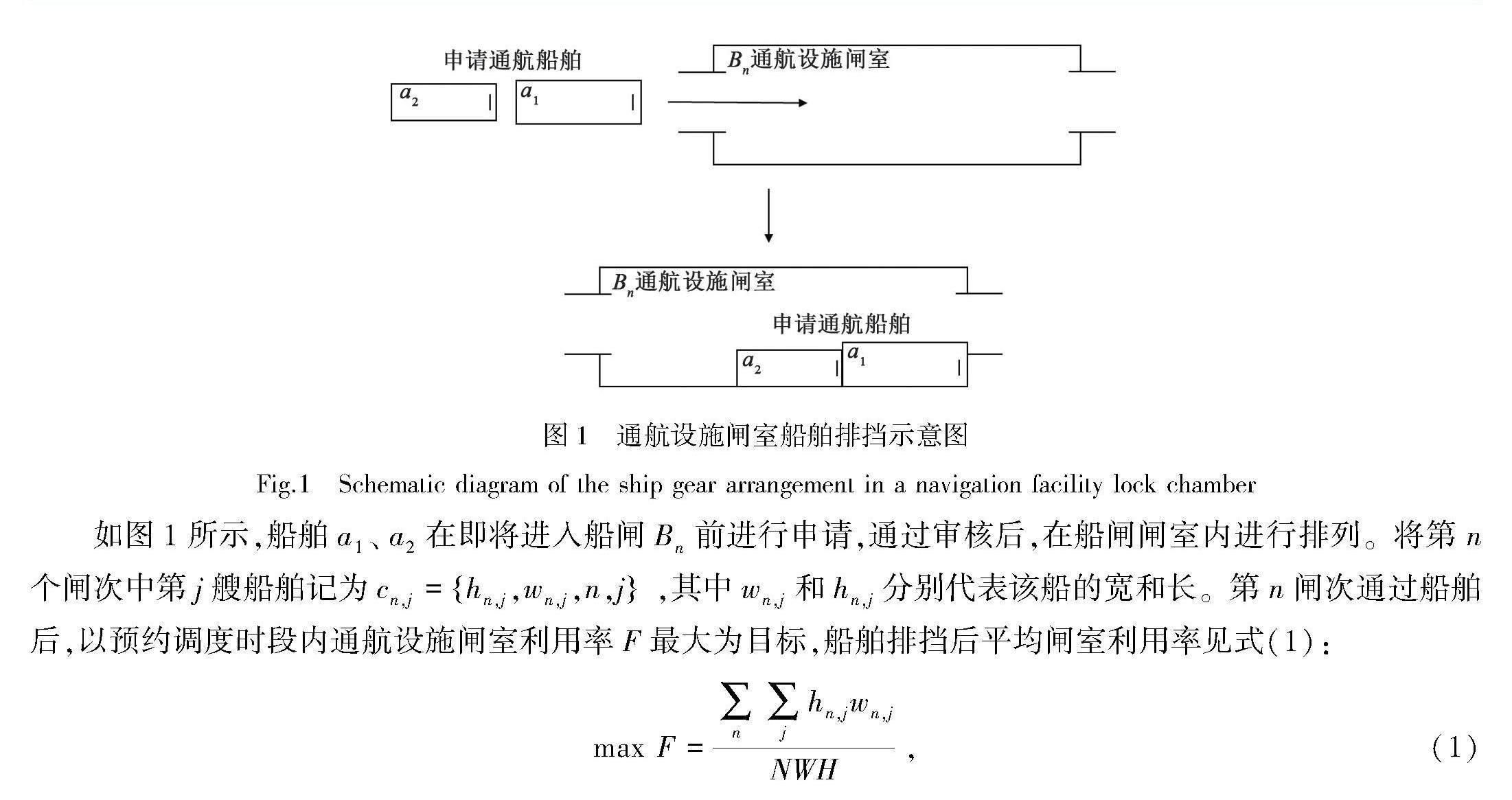
船舶在通航设施闸室进行排挡时,需要遵守船头在前的规定,在闸室内时不能进行180°反转或90°转置。以船舶自左向右通行为例,船舶从闸室左侧进入,右侧驶出,通航设施中船舶闸室排挡示意见图1。
如图1所示,船舶a1、a2在即将进入船闸Bn前进行申请,通过审核后,在船闸闸室内进行排列。将第n个闸次中第j艘船舶记为cn,j=hn,j,wn,j,n,j,其中wn,j和hn,j分别代表该船的宽和长。第n闸次通过船舶后,以预约调度时段内通航设施闸室利用率F最大为目标,船舶排挡后平均闸室利用率见式(1):
max F=∑n∑jhn,jwn,jNWH ,(1)
其中,N表示闸次数量,当每个闸室的利用率达到最大时,可使需要使用的总闸室数量最少。因此,可以将问题转化为求解二维装箱问题。
2 船舶闸室连续排挡问题模型
2.1 二维装箱问题模型
船舶闸室排挡问题类似于二维装箱[14]问题,二维装箱问题是指将一组二维矩形物体装入最少数量的二维箱子。二维装箱问题是NP(non-deterministic polynomially)难问题,即没有已知的多项式时间算法可以解决它。因此,通常使用启发式算法、贪心算法、分支定界算法等来解决这个问题。二维装箱问题在生产和物流领域有广泛的应用,例如货物装箱、板材下料、纸张裁剪等。
通航设施闸室分配问题类似于二维装箱问题的2BP(2D bin packing)问题。在2BP问题中,待装物体可以是规则的几何图形,也可以是不规则的多边形。该问题的目标是将一组大小不等的矩形物体排列在若干大小相等的矩形箱子中,以最小化使用的箱子数量为目标。物体的摆放需满足物体不超出箱子边界,且物体边缘需平行于箱子边缘;箱中物体两两互不重叠两个约束条件。二维矩形装箱问题示意图见图2。
如上图所示,二维装箱问题的2BP问题中,aB,i表示第i个矩形物品,aB,i=wB,i,hB,i,i,其中wB,i和hB,i分别表示矩形物体aB,i的长和宽。箱子宽度和高度定义为WB和HB将放入第n箱子的第j矩形物体的左下角坐标表示为xL,n,j,yL,n,j,右上角表示为xR,n,j,yR,n,j,目标函数为满足所有物体填装的最少使用箱数min F=n。
通过上述规则和符号定义,对2BP问题建立约束,以箱子左下角为原点的笛卡尔坐标系,箱子的右下角、左上角、右上角坐标分别表示为WB,0、0,HB、WB,HB,对2BP问题进行建立满足要求的约束函数,如下:
0≤xL,n,j≤WB|HB, 0≤xR,n,j≤WB|HB,(2)
0≤yL,n,j≤WB|HB, 0≤yR,n,j≤WB|HB,(3)
xR,n,j-xL,n,j,yR,n,j-yL,n,j∈WB,HB,HB,WB,(4)
xL,n,m-xR,n,j, xL,n,m-xR,n,i, yL,n,m-yR,n,j, yL,n,j-yR,n,m≥0 ,(5)
其中,式(2)、式(3)表示矩形物体不能超出箱子边界;式(4)表示矩形物体应与箱子正交,即矩形的4条边都与箱子平行;xL,n,m,yL,n,m表示箱子中已存在的矩形物体m左下角坐标,式(5)表示放入箱子的矩形物体不能与原箱中物体重叠。
2.2 船舶闸室排挡问题模型
船舶闸室排挡模型是以二维装箱模型为基础,在二维装箱模型的描述中,模型中需要放置进箱子中的矩形物体可以转置,矩形物体进入箱子的顺序可以任意打乱,对于船舶在闸室中的排挡模型而言,船舶通航在确定优先级之后应该服从FCFS(first come first serve)规则,但是服从FCFS规则的船舶可能会降低闸室利用率。船舶进入通航设施的目的是通过通航设施,所以,在进入通航设施闸室时,只能船头先进入闸室,不能进行任意反转。
以二维装箱问题模型为基础进行改进,建立以二维装箱模型为基础的船舶闸室排挡问题模型,相对于二维装箱问题,船舶闸室排挡问题具有以下特点:
(1)船舶在闸室内无法进行180°反转和90°转置排列,在模型中仅表现为无法进行90°转置;
(2)在预约通航阶段可通行闸次确定,船舶在当前调度周期内无法排挡时,需要安排进下一个调度周期进行排挡;
(3)船舶排挡位置确定后,需要生成船舶进入闸室方案。
以二维装箱问题模型为基础,对船舶闸室以左下角为基础,建立笛卡尔坐标系。船舶闸室排挡模型见式(6)~(9):
0≤xn,j≤W,0≤xn,j+wn,j≤W ,(6)
0≤yn,j≤H,0≤yn,j+hn,j≤H ,(7)
wn,j,hn,j∈W,H ,(8)
xn,k-xn,j,xn,k+wn,k-xn,j+wn,k,yn,k-yn,j,yn,k+hn,k-yn,j+hn,k≥0,k>j>0 ,(9)
式中,xn,j,yn,j表示在闸室n中第j艘船舶的左下角坐标;wn,j和hn,j分别表示在闸室n中第j艘船舶的长度和宽度;xn,k,yn,k表示闸室中已有的第k艘船舶左下角的坐标。式(6)~(7)表示船舶不能超出闸室边界;式(8)表示船舶长和宽只能平行于闸室的长和宽;将闸室中已有船舶长和宽分别记为wn,k和hn,k,式(9)表示新置入船舶和闸室内已有的船舶不能重叠。
3 船舶排挡模型求解算法及流程
3.1 船舶排挡模型求解
二维装箱问题是指在给定一定数量的物品和若干个尺寸相同的箱子的情况下,如何将所有物品装入尽可能少的箱子中。常用的固定型二维装箱问题求解算法包括Best Fit算法、First Fit算法,二者都是经典的启发式算法,其思想都是在每个箱子中尽量放入更多的物品,从而减少箱子的数量。Best Fit算法将所有待装箱物品按照宽度从大到小排序,然后依次将每个物品放入当前剩余空间最小的那个箱子中;而First Fit算法则是将所有待装箱物品按照宽度从大到小排序,然后依次将每个物品放入第一个可以容纳它的箱子中,如果没有箱子可以容纳该物品,则新开一个箱子。
船舶闸室排挡问题模型和二维装箱模型存在差异,为求解船舶闸室排挡问题,在进行船舶闸室排挡模型求解时,以贪婪策略思想为基础。贪婪策略是一种常见的算法思想,具体是指,在对问题求解时,总是做出在当前看来是最好的选择。对于船舶闸室排挡模型而言,不从整体最优上加以考虑,虽然在某种意义上可能会得到问题的局部最优解,但是由于闸次排挡并无后效性,即当前模型的状态与之前或之后的模型状态无关,只与当前状态有关,所以贪婪策略可以适用。
在船舶闸室排挡模型中,将可调度优化时段内的每一个闸次船舶位置和船舶数量的求解当作子问题,进行逐次求解。当所有的闸次中船舶数量均为最大可置入量,且所有船舶均被排挡时,子问题的结果组合起来即为所有预约船舶的通航排挡闸次结果,此时闸次的使用量可以认为是最少的。
以船舶通过通航设施以由左向右的方式通航,排挡过程可以分为3个步骤:
(1)将需要船舶由左上角向右,向下放入闸室内,在放入船舶之后,将剩余闸室空间分为两个空间碎片,由于一般通航设施闸室横向长度远大于纵向,在船舶闸室排挡中采取纵向分割方式,将未利用的闸室空间分为两个空间碎片,闸室内没有其他船舶时的排挡空间碎片划分方式见图3。如图3所示,当第一艘船舶a1进入通航设施闸室B后,由于闸室将其放入通航设施闸室的右下角,对空间纵向分割,为空间碎片1和空间碎片2,此时空间碎片1面积大于空间碎片2面积。
(2)当闸室中已经存在船舶时,闸室空间会存在多个被纵向切割的空间碎片,将空间碎片由小到大依次与当前需要排挡船舶的大小进行对比,当出现第一个可放置当前船舶空间时,将船舶由空间碎片左上角向右、向下放入闸室中,若所有空间碎片均无法放置当前需要排挡船舶时,当前闸次船舶排挡结束。闸室存在船舶时当前船舶排挡方法见图4。如图4所示,船舶a1的空间碎片划分完成后,当船舶a2所需占用的面积小于空间碎片2大小时,将船舶a2放置入空间碎片2中,若船舶a2所需闸室空间占用面积大于空间碎片2且小于空间碎片1时,将船舶a2置入空间碎片1中。当船舶a2进入闸室后,需要重新进行空间碎片的划分,若闸室空间存量大于最小船舶长度,依旧进行纵向划分,如图4(a)所示。若不大于最小船舶长度,则进行横向分割,如图4(b)所示。
(3)单一闸次装箱结束后,将闸次排挡后的船舶数量存储,随后对下一个闸次进行装箱,依次计算所需数据,依次存储。在进行计算时,对船舶闸室建立二维笛卡尔坐标系,按照改进二维装箱模型的船舶闸室排挡模型建立约束。模型的求解主要包括第一艘船舶入闸、空间碎片划分和船舶空间碎片比较三个部分。
模型的计算如下:当前闸次内第1艘船舶ai入闸时,船舶的长度为hi,宽度为wi,闸室的长宽记为W,H,令x1,k+w1,k=W,h1,k=0,将船舶放入闸室右下角,船舶左下角的坐标为W-w1,k,0。
空间碎片以纵向方式划分,存在的两个空间碎片,将第m个空间碎片位置表示为wL,m,k,hL,m,k,wR,m,k,hR,m,k,分别表示为空间碎片的左下角坐标和右上角坐标。如当第1艘船舶放置后,存在的两个空间碎片分别为0,0W-w1,k,H和W-w1,k,h1,kW,H,后续待闸船舶依照此规则再依次对每个船舶进行位置计算,当一个闸次内船舶数量充足,无法放入后续待闸船舶时,进入下一个闸次的船舶拍档计算。
3.2 船舶排挡模型求解
采用上文求解方法,在进行考虑船舶顺序过闸时船舶闸室连续排挡模型中,将船舶按照到达次序以FCFS的规则进行排挡处理。通过船舶入闸信息A=a1,a2,…,ai得到预约通航船舶的入闸顺序和每艘船舶的安全距离。
根据上述模型及求解方法,考虑船舶顺序过闸船舶连续闸次排挡模型求解流程见图5。
如图5所示,在进行船舶排挡之前,首先对需要排挡船舶的优先级进行确认,得到船舶入闸实际顺序,随后依照安全距离计算方法对船舶进行安全距离计算,在本文的仿真中,这个过程不进行体现。
得到船舶实际在闸室中所需占用的空间大小以及入闸顺序后,当闸室中无其他船舶存在时,将待闸船舶按照排挡规则置入空闸室中,随后进行空间碎片划分,将剩余空间纵向划分为两个空间碎片,与下一艘待闸船舶所需占用空间大小进行对比,确认船舶可置入的位置,并划分新的空间碎片,除第一艘船舶以外,其他船舶置入后均进行空间碎片划分,若所有空间碎片无法满足下一艘待闸船舶入闸时,即使后续船舶存在可以装入当前闸室船舶,不考虑将其排挡入当前闸次,当前闸次船舶排挡结束,进行下一个闸次排挡。所有闸次排挡结束后,输出所有闸室排挡信息和船舶在闸室内排挡位置。
3.3 不考虑船舶顺序过闸连续排挡算法
不考虑船舶顺序过闸的排挡方法是指当提前获得所有船舶到闸信息A=a1,a2,…,ai后,当闸室内没有船舶时,将待闸中编号最小的船舶按照排挡规则放置入闸室内,随后按编号顺序,将后续所有船舶与闸室中存在的空间碎片进行比较,若存在空间碎片可以放置,则在空间碎片中放入该船舶,若无法放置,则依次判断下一艘船舶是否可放入闸室内。
不考虑船舶过闸顺序的船舶连续排挡算法求解流程见图6。
如上图所示,不考虑船舶顺序通航的船舶闸室排挡算法中,当下一艘船舶无法在当前闸室中进行排挡后,会依次对后续船舶进行排挡处理,直到所有船舶计算完毕,在当前闸室内放入所有可过闸船舶后,才会进行下一个闸次的船舶排挡计算。其他排挡步骤与考虑船舶顺序通航的连续排挡算法相同。
4 仿真实验
为验证本文算法,采用百色枢纽通航工程数据进行计算,百色枢纽通航工程通航设施由25 m水头差的省水船闸、长度约4 km的中间渠道、提升高度88.8 m的全平衡钢丝绳卷扬垂直升船机组成,线路全长约4 384 m。闸室效尺寸为111.0 m×12.0 m×4.7 m(长×宽×水深),设计年单向通过能力为6.02×106 t。百色枢纽通航工程建成后构想见图7。
由于百色枢纽通航工程尚未完工,随机船舶信息进行排挡,百色枢纽通航工程中预计通航船舶的信息及各种船型比例见表1。
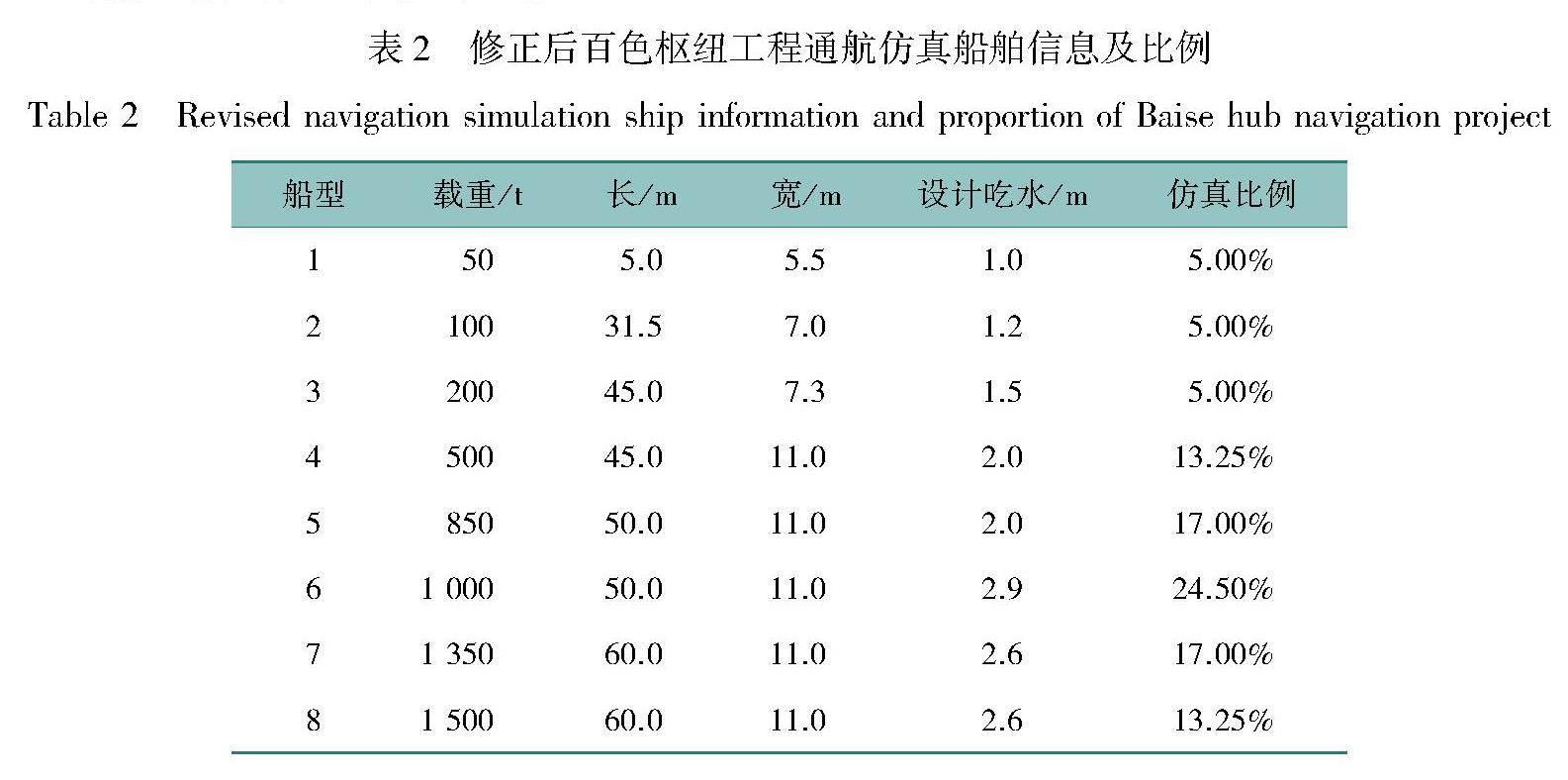
由于在预期船舶闸室占比中,小型船舶被划分入大中型船舶中,对此进行修正,并且考虑到未来可能会存在执法船等小型船舶通过通航设施,增加其他小型船舶信息,将其他小型船舶设置的占比为总到闸船舶数量的15%修正后船型信息及比例见表2。
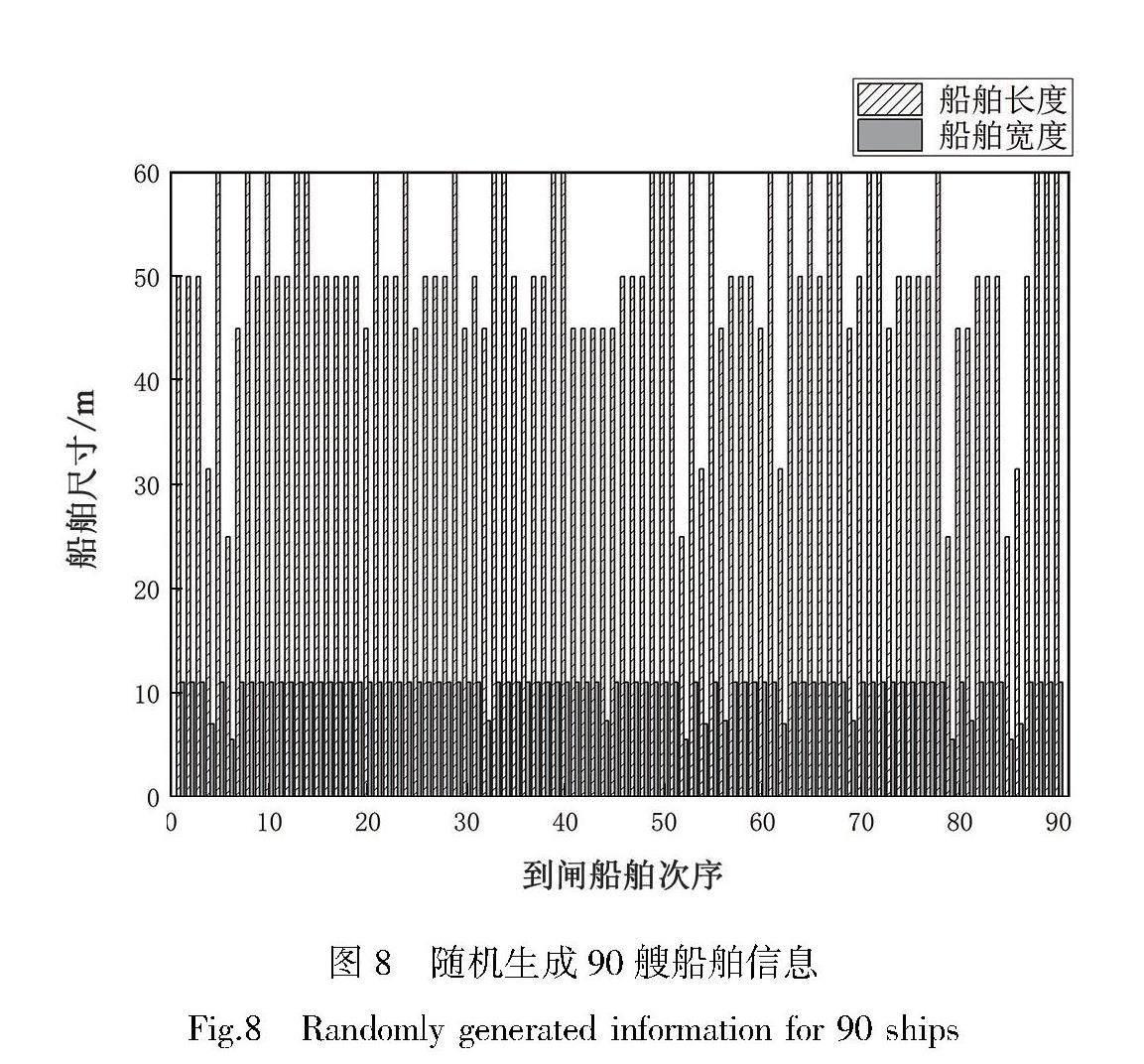
按照百色枢纽工程通航仿真船舶信息及比例,生成90艘船舶信息,并按照生成顺序进行排列,随机生成的船舶信息见图8。
考虑船舶到闸顺序,采用模型及算法对船舶进行排挡,排挡后结果见图9(a)。闸室平均占用率为76.424%,需要47个闸次放行所有船舶。不考虑船舶到闸顺序,采用模型及算法对船舶进行排挡,排挡后结果见图9(b)。闸室平均占用率为76.821%,需要45个闸次放行所有船舶。根据求解结果可以看到,模型在考虑船舶到闸顺序和不考虑船舶到闸顺序两种情况下都具有较好的求解能力。
在考虑船舶到闸顺序的情况下,闸室的利用率较高,但仍存在一定的空闲空间。这是因为在这种情况下,优先考虑公平服务,对闸室填充效果相对不那么关注。因此,船舶可以自由进出闸室,没有进行预约的要求。然而,由于船舶之间的到闸顺序不同,可能会导致一些闸室在某些时间段内没有充分利用,从而浪费了一部分资源,这种入闸模式船舶较少时,且通过时间不确定的情况。
相比之下,在不考虑船舶到闸顺序的情况下,闸室的利用率相对更高。这是因为在这种情况下,船舶可以按照先到先得的原则进入闸室,充分利用闸室资源。然而,由于忽视了船舶到闸顺序的因素,当多艘船舶同时到达闸室时,可能由于改变船舶入闸队列,导致船舶之间的冲突和拥堵情况增加。
5 结论
本文利用二维装箱模型,建立了船舶闸室排挡模型,并提出一种以贪婪策略为基础的求解船舶闸室连续排挡模型的算法,最后进行仿真实验,根据仿真结果可以得到如下结论:
(1)船舶闸室连续排挡模型及求解算法可以有效对船舶进行闸室排挡;
(2)考虑船舶到闸顺序的排挡方法与不考虑船舶到闸顺序的排挡方法均可以采用本文提出的船舶闸室连续排挡模型进行求解;
(3)不考虑船舶到闸顺序的排挡方法可以更高效地使船舶进行通航,考虑船舶到闸顺序的排挡方法更具有公平性,可以在实际工作中根据需求灵活采用不同方法进行排挡。
参考文献:
[1]季彬. 水利枢纽船舶过闸—泊位联合调度模型与方法研究[D]. 武汉: 华中科技大学, 2018.
[2]GOLIAS MM, BOILE M, THEOFANIS S. Berth scheduling by customer service differentiation: a multi-objective approach[J]. Transportation Research Part E: Logistics and Transportation Review, 2009, 45(6): 878-892. DOI: 10.1016/j.tre.2009.05.006.
[3]YUAN Y B, JI B, YUAN X H, et al. Lockage scheduling of Three Gorges-Gezhouba Dams by hybrid of chaotic particle swarm optimization and heuristic-adjusted strategies[J]. Applied Mathematics and Computation, 2015, 270: 74-89. DOI: 10.1016/j.amc.2015.08.009.
[4]GOLIAS MM, BOIL M, THEOFANIS S, et al. A multi-objective decision and analysis approach for the berth scheduling problem[M]//Project Management Techniques and Innovations in Information Technology. Pennsylvania: IGI Global, 2012: 1-20. DOI: 10.4018/978-1-4666-0930-3.ch001.
[5]邓伟, 邝祝芳, 余绍军, 等. 基于遗传算法的三峡-葛洲坝船闸闸室编排算法[J]. 人民长江, 2016, 47(24): 55-59. DOI: 10.16232/j.cnki.1001-4179.2016.24.012.
[6]王伟, 黄涛. 基于随机排挡的船闸通过能力研究[J]. 水运工程, 2021(1): 162-167. DOI: 10.16233/j.cnki.issn1002-4972.20201228.035.
[7]ZHANG D F, SHI L Y, LEUNG S C H, et al.A priority heuristic for the guillotine rectangular packing problem[J]. Information Processing Letters, 2016, 116(1): 15-21. DOI: 10.1016/j.ipl.2015.08.008.
[8]BAKER B S, COFFMAN E G Jr, RIVEST R L. Orthogonal packings in two dimensions[J]. SIAM Journal on Computing, 1980, 9(4): 846-855. DOI: 10.1137/0209064.
[9]CHAZELLE. The bottom-left bin packing heuristic: an efficient implementation[C]. IEEE Transactions on Computers. 1983, 32(8): 697-707. DOI: 10.1109/TC.1983.1676307.
[10]BURKE E K, KENDALL G, WHITWELL G. A new placement heuristic for the orthogonal stock-cutting problem[J]. Operations Research, 2004, 52(4): 655-671. DOI: 10.1287/opre.1040.0109.
[11]阳名钢, 陈梦烦, 杨双远, 等. 求解二维装箱问题的强化学习启发式算法[J]. 软件学报, 2021, 32(12): 3684-3697. DOI: 10.13328/j.cnki.jos.006161.
[12]李泳龙, 吴礼国, 周定科. 基于多种排挡策略的船闸通过能力仿真研究[J]. 水运工程, 2023(S1): 119-124. DOI: 10.16233/j.cnki.issn1002-4972.20230104.050.
[13]甘金明, 吴洁明. 船闸调度信息管理及闸室排挡调度优化设计[J]. 梧州学院学报, 2014, 24(3): 1-6. DOI: 10.3969/j.issn.1673-8535.2014.03.001.
[14]ZHANG X P, FU X D, YUAN X H. Co-evolutionary strategy algorithm to the lockage scheduling of the Three Gorges Project[C]//2008 IEEE Pacific-Asia Workshop on Computational Intelligence and Industrial Application. Wuhan, China: IEEE, 2009: 583-587. DOI: 10.1109/PACIIA.2008.347.

