复合翼飞行器动力旋翼系统的力学建模及应用

杜伟 陈伯建 程海涛 李哲舟 王泽昭

DOI：10.3976/j.issn.1002-4026.20230124

收稿日期：2023-08-27

基金项目：国家电网有限公司总部科技项目（5500-202321181A-1-1-ZN）

作者简介：杜伟（1982—），男，硕士研究生，高级工程师，研究方向为直升机、无人机输电线路运检技术。E-mail：du-wei@sgst.sgcc.com.cn

*通信作者，王泽昭（1998—），男，工程师，研究方向为输电线路运维、变电站无人机电力巡检。Tel：13651029132，E-mail：eminent_wzz@163.com

摘要：以某60 kg级复合翼飞行器的旋翼和推进螺旋桨为对象，以片条理论和动量理论为依据，循环求解桨前速度增量，结合地面试验数据修正螺旋桨力学模型，得到螺旋桨的力学性能。模型计算结果显示，推力计算偏差小于5%，功率计算偏差小于10%。由此计算螺旋桨在一定来流下的推力与转速和控制参数的特性曲线，建立螺旋桨与控制参量之间的关系，以支持复合翼飞行器动力模型研究。

关键词：复合翼；动力建模；片条理论；推力MAP

中图分类号：V212.4    文献标志码：A    文章编号：1002-4026（2024）03-0093-10

开放科学（资源服务）标志码（OSID）：

Mechaical modeling and application of a combined

wing aircraft dynamic rotor system

DU Wei1，CHEN Bojian2，CHENG Haitao1，LI Zhezhou2，WANG Zezhao1*

（1.State Grid Power Space Technology Co.， Ltd.，Beijing 102209，China; 2. Electric Power Research Institute，State Grid Fujian Electric Power Co.， Ltd.，Fuzhou 350007，China）

Abstract∶In this study， we build a model for the rotors and propellers of 60 kg combined wing aircraft based on the strip and momentum theory， and circularly calculated the increment of the upcoming flow as an intermediate variable to precisely determine the propellers performance. By comparing the obtained results with the experimental data， we corrected the model and calculated the mechanical performance of the propeller. Result showed that the model could evaluate the thrust and shaft power with a bias of less than 5% and less than 10%， respectively. Using this method， we drew the MAP curves representing the mechanical performance as the essential parameters in the power model and built a bridge between mechanical performance and controlling model. The results can support the study of mechanical modelling of combined wing aircraft.

Key words∶combined wing aircraft； power modelling； strip theory； thrust MAP curves

在民用无人机市场，由于复合翼飞行器兼具固定翼经济性和多旋翼机动性的特点而广受市场欢迎。在电力巡检方面，我国电网覆盖面广，线路距离长，地形复杂多样，给电力巡检人员的工作带来较大困难和挑战。使用无人机进行电力巡检不仅能够解决地形复杂带来的巡检困难，而且能够减轻巡检人员的工作强度。

复合翼飞行器多见于200 kg级以下的无人机系统，动力系统主要依靠螺旋桨提供的升力和推力，动力建模的主要难点是建立螺旋桨的力学模型。刘沛清等［1-2］提出了计算螺旋桨的理论分析方法。夏贞锋［3］采用数值模拟的方法研究螺旋桨的滑流特性。文献［4-8］研究飞行力学建模和控制系统算法，较多关注飞行器本身的力学需求，对动力系统的模型说明较少。王乐乐［9］基于SimMechanics研究飞行器的飞行动力学模型。王春阳等［10］在涵道式垂直起降固定翼平台上研究了无人机纵向稳定性。伊朝阳［11］鉴于共轴双桨飞行器的复杂性研究了控制系统的模型。冯姣［12］基于Web平台研究飞行仿真系统。聂营等［13］采用数值仿真和实验结合的方法研究螺旋桨的力学参数。裴思宇［14］采用叶素理论的方法研究微小型旋翼飞行器螺旋桨在流动情况下的受力。丁倩岚［15］采用实验结合数值仿真的方法研究无人机螺旋桨气动性能。张航等［16］在统计大量电动无人机动力系统特性后建立电动动力系统模型。王刚等［17］基于高效的电机螺旋桨匹配设计方法研究电动无人机的航时。文献［18-22］主要研究了电动固定翼单升力系统或单推进系统无人机建模、匹配及优化设计。对于复合翼以及油电混合动力系统的动力模型，文献从能量消耗角度，基于动力系统元件参数进行多旋翼动力系统匹配优化并简化电调和电池等能源系统元件的模型［23-24］。

综上所述，当前公开发表的文献主要研究动力系统的控制特性以及能源系统与动力系统的交联匹配优化设计，较少关注复合翼构型的多旋翼系统和油动推进系统的全动力系统的力学模型。螺旋桨力学性能计算作为动力系统设计的关键环节，也是匹配优化设计以及动力建模工作的重要组成部分，而螺旋桨具有复杂气动特性的特点往往需要采用试验和计算流体力学（computational fluid dynamics， CFD）仿真相结合的方法进行研究，本身计算量较大，需要的时间较长，不利于工程人员的快速设计，而单纯使用叶素理论进行螺旋桨力学性能计算会导致结果误差较大。对于一般的工程验算和无人机系统设计的前期匹配分析，CFD仿真计算和叶素理论均不利于直接应用于工程计算［2］。

基于上述CFD仿真计算和叶素理论计算的缺点，本文直接从复合翼飞行器多桨系统的力学性能出发，区别于文献［2］所采用的计算螺旋桨桨前干涉角的方法，采用螺旋桨片条理论的方法直接循环求解桨前速度增量得到螺旋桨动力装置的力学性能，进而建立螺旋桨的力学模型，以便于设计人员快速地利用模型进行动力建模和螺旋桨气动性能的计算分析。

1  复合翼升力系统与推进系统的组成

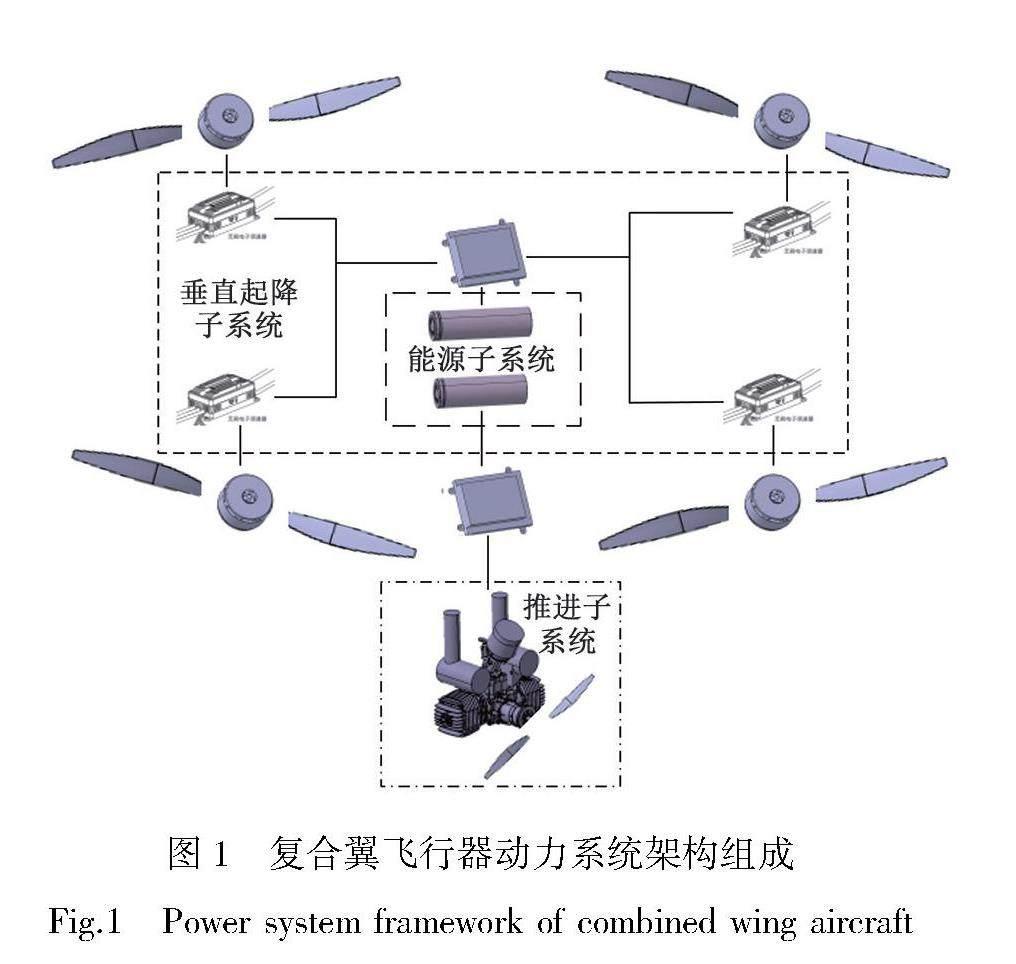
复合翼飞行器动力系统的垂直起降升力子系统为电力驱动装置，具有较好的控制特性，而固定翼模式下的推进装置可采用油动发动机或电动螺旋桨，两者本质均为螺旋桨推进装置。本文的研究对象为要求飞行时间大于4 h的复合翼飞行器，动力系统架构主要由垂直起降子系统和推进子系统组成。其中垂直起降子系统由4个相互独立的升力单元组成，每个升力单元包括电调、电机、螺旋桨，电机驱动旋翼螺旋桨提供升力，用于起降和应急情况，电功率由能源子系统供给。油动推进子系统由发动机控制系统及动力装置组成，发动机驱动螺旋桨提供前进推力，其动力总架构如图 1所示。本文主要研究如何建立动力系统关联的螺旋桨的力学模型，其他系统不做介绍。

以四旋翼为例：设每个旋翼产生的合力方向的力可表示为F1、F2、F3、F4。对于推进系统，多数复合翼飞行器的推进装置由单个动力组成，设产生的驱动力为Ft。飞行器的综合阻力为Drag，气动升力为Fl，重力G，飞行器质量为m。为简化分析，假设飞行器质量不随时间变化，应用飞行力学知识，则飞行器的动力学方程可表示为：

mV·=∑4i=1Fi+Ft+G+Drag+Fl ，（1）

将上述力学方程在机体坐标系（x，y，z）三个方向上展开，如下：

mVx·=∑4i=1Fix+Ftx+Gx+Dragx+Flx

mVy·=∑4i=1Fiy+Fty+Gy+Dragy+Fly

mVz·=∑4i=1Fiz+Ftz+Gz+Dragz+Flz。（2）

设各螺旋桨的安装角度相对飞机x轴、y轴、z轴可设为θ、ψ、φ。定义绕轴逆时针方向为正。则旋翼螺旋桨的力学分量系数矩阵：

A=

cosθ1cosψ1cosφ1

cosθ2cosψ2cosφ2

cosθ3cosψ3cosφ3

cosθ4cosψ4cosφ4

cosθtcosψtcosφt ，（3）

考虑到多旋翼安装的对称性，有：

θ1=θ2，θ3=θ4，θ1=π-θ3

ψ1=π-ψ2，ψ2=ψ3，ψ1=ψ4

φ1=φ2=φ3=φ4 ，（4）

上述矩阵A可以重整为：

A=cosθ1cosψ1cosφ1

cosθ1cos（π-ψ1）cosφ2

cos（π-θ1）cos（π-ψ1）cosφ3

cos （π-θ1）cosψ4cosφ4

cosθtcosψtcosφt，（5）

在旋翼系统与推进动力同时工作的过渡段，螺旋桨动力系统完整的力学表达为：

Fth=F1F2F3F4FtAijk。（6）

系数矩阵中的角度变量θ1、ψ1、φ1以及θt、ψt、φt为螺旋桨安装角度，与旋翼的布置有关，则系数矩阵A已知。因此，对螺旋桨的力学参数的求解直接影响动力模型的准确性。

2  螺旋桨片条理论建模

螺旋桨流场特性复杂，采用螺旋桨片条理论进行螺旋桨力学性能估算可以实现快速的匹配计算。根据文献所述，螺旋桨升力或拉力、功率、拉力系数、功率系数分别用TP，P，Ct，Cp表示［1］，表达式如下：

Ct=TPρn2D4，（7）

Cp=Pρn3D5，（8）

其中，ρ为气流密度，n为螺旋桨转速，D为螺旋桨直径。为不失去一般性，螺旋桨拉力用TP表示，不区分推进螺旋桨和升力螺旋桨。片条理论应用于螺旋桨推力计算的主要难点在于得到桨前速度。根据动量理论的结论，桨前速度增量为桨后滑流速度增量的0.5倍［2］。设V0为桨前来流，u2为桨后滑流速度的增量，则螺旋桨拉力可表示为：

TP=ρAp（V0+12u2）u2，（9）

其中，Ap为桨盘面积。由公式（9），静止条件下，桨前来流V0为0，则桨前速度增量为：

ΔV=12u2=12  2TPρAp。（10）

在正常的飞行过程中，桨前来流V0不为0，则桨前速度增量为：

ΔV=12u2=12（  V20+2TPρAp-V0），（11）

根据公式（11），V0增大，桨前速度增量逐渐减小，速度增量逐渐弱化。

桨前实际速度统一表示为：

V1=V0+ΔV。（12）

在本模型中，桨前气流速度并非以远场速度为初始值，而是以滑流速度的增量为初值。结合动量理论的结论，对螺旋桨做如下简化：

（1）螺旋桨的推力主要来源螺旋桨叶素升力分量，桨后下游较远位置的非定常流动以及强烈的旋流特征产生的附加阻力不考虑。

（2）气流作用于螺旋桨桨盘产生的垂直方向流动是均匀的，桨前入流速度是统一的。

（3）叶素模型计算时由于径向方向转速相同，则径向的线速度差别不大，在一定速度范围内认为螺旋桨扰流流动相似。

（4）桨叶在旋转中的微小气动弹性变形对结果影响较小，计算时不考虑由于变形导致的安装角度变化。

据上述理论需要，获取螺旋桨叶素结构参数。叶素测量数据定义如图 2所示。叶素弦长为b，叶素安装角为β，Ω为叶素旋转角速度，r为叶素旋转半径，R为螺旋桨的旋转半径。定义叶素当地无量纲相对长度Rel：

Rel=rR。（13）

根据公式（13），容易得Rel∈［0，1］。对于已知的螺旋桨，根据上述方法可得到某螺旋桨的叶素安装角和弦长的分布。散点数据和拟合分布关系如图 3所示。红色曲线为采用多项式函数曲线拟合的近似曲线，离散数据偏离拟合曲线的主要原因是测量手段和工具精度不高，提高测量精度不是本文研究的重点。本文认为曲线趋势反映真实的螺旋桨结构特性，后面的分析均基于叶素安装角和弦长分布关系。

使用叶素计算螺旋桨的力学参数时，根据螺旋桨厂家提供的Clark-Y翼型，在Profili数据库中的查询翼型气动特性的极曲线，以此作为螺旋桨气动数据。由于计算量较大，在Matlab环境编写螺旋桨片条模型程序，完成螺旋桨气动特性计算，得到螺旋桨拉力、功率、功率系数、拉力系数、扭矩等参数与转速的特性曲线关系。在Matlab中建立的螺旋桨模型计算流程如图4所示。

由计算分析流程可知，应用叶素片条理论计算时，需要预设桨前速度增量u0。为避免产生误解，公式（10）和公式（11）中的速度增量ΔV在流程中为U0，两者计算方法相同，流程中的δ表示设置收敛因子。在飞行条件下，螺旋桨的桨前气流设为真空速，使用V0表示。为避免方程在地面静风即来流速度为0时出现奇点（需符合连续性方程），计算开始前需预先设置螺旋桨桨前气流速度V′以启动流程。关于流动连续性假设可参看文献［2］。本文认为，在V0为0时，螺旋桨桨前远场速度很小，靠近螺旋桨桨盘位置流速逐渐增大，因此V′应设置一个小量。基于上述分析，预设桨前流速可克服程序中的奇点问题。对于螺旋桨前存在一定速度的来流时，由于预设的来流速度V′相比来流速度V0为小量，对螺旋桨性能影响较小。由此，可据图4所示的流程计算螺旋桨静推力（来流速度为0时的推力）和动推力（来流速度不为0时的推力），达到评估螺旋桨性能的目的。

图4的流程所示，螺旋桨力学性能参数和驱动设备的控制参数均为本模型的两个重要的输出量。在实际应用中，飞行控制专业设计人员在进行控制率设计时需依据当前螺旋桨的力学特性结合飞行状态解算速度环的控制参数，因此动力专业设计人员有必要给出飞行状态下动力模型的基本控制量，而联合螺旋桨性能和驱动螺旋桨设备模型F（ns，M）可得到必要的控制参数。本文在引用螺旋桨驱动设备模型时认为其已知。

3  理论计算及试验数据对比

根据文献［2］中的结论，桨叶根部在相对长度0～0.25之间产生的推力较小，因而只计算0.25～1.00的叶素推力。得到了在典型工况下的单位长度上的叶素推力，结果如图 5所示。

在螺旋桨桨叶的无量纲长度上，推力主要集中在相对长度0.6～0.9，低半径位置叶素推力较小。随着转速的增大，推力的集中程度越高。在低转速范围，推力的分布比较平缓，该计算的结果总体上符合文献［2］的结论。另外，从图中的结果得出，转速推力特性曲线在0.25～1.00并非连续，而是存在小的阶跃断点，断点总体分布在0.5～0.6。分析认为，产生该现象的主要原因是扭转的桨叶在径向分布上安装角差异较大，在忽略气流沿径向方向上的干扰流动后，各位置的桨叶迎角差异较大，在某个长度位置迎角突变，导致升力系数等参数取值偏离，该误差与理论模型准确度有关。总的来说，计算的叶素推力符合已知螺旋桨结论，结果合理。将模型计算的螺旋桨的总推力与测试数据对比。其中表1所示的测试数据均由图 6所示的推力扭矩试验台测取。两种规格桨的试验数据与计算数据结果对比如图 7所示，其中Ts、Te以及Ps、Pe分别表示螺旋桨推力和功率的模型计算值和试验值。

由图 7（a）分析，在全部转速范围内，螺旋桨总的推力计算结果与测试数据比较符合。图 7（b）所示，计算功率随着转速的提高与测试的螺旋桨轴功差异逐渐增大，且主要集中在高转速区域，最大误差，而在低转速范围内，计算功率符合性较好。由曲线可知，对26×18两叶桨，转速低于4 000 r/min时，计算功率与实测符合较好，对28×18两叶桨，转速低于4 500 r/min时符合较好。

4  螺旋桨力学性能及复合翼动力模型

为了更好地对比分析上述计算结果和测试数据的差异。将图 7所示的螺旋桨推力和轴功相对误差整理成如图 8所示散点分布图。

定义计算功率的相对误差Er：

Er=Ps-PePe×100%，（14）

其中，Ps以及Pe与前文定义相同。按公式（14）类似定义计算推力相对误差。图 8中的进距比J表征螺旋桨桨前来流速度与螺旋桨最大位置处的旋转速度比的度量，定义为式（15）：

J=V0Dn，（15）

其中，n为螺旋桨转速。由图 8可知，当J大于0.07时，螺旋桨功率计算结果误差小于10%，且J越大计算的误差越小。在高转速区，来流速度很小，转速提高，进距比降低，叶素迎角会逐渐增大，较大的气流迎角可能导致气流分离。由图8所示，螺旋桨计算推力与实际测试数据的偏差始终保持在5%以内，但偏离特性特征不明显。考虑到本模型不能预测气流分离时的阻力特性，在较低的转速范围内，桨前气流迎角较小，翼型叶背流动分离特性不明显，模型能较好地估计螺旋桨的功率。当桨叶安装角度越大，在高转速区分离的趋势越明显，理论估计功率的误差也越大，但在全转速范围内，理论估计的推力符合较好。对此限定本模型使用范围，以确保在使用的范围内具有一定的估计精度。

在正常的飞行中，一般有进距比J∈0.4，0.8，其值远远大于0.07。因此，本文认为当J>0.07时，模型计算的功率误差小于10%，推力误差小于5%，满足一般工程计算且不至于明显偏离实际情况。据此可以说明采用直接循环求解桨前速度增量计算螺旋桨性能是可取的，本文建立的螺旋桨的力学模型具有一定的准确性。在图 4所示的计算流程中，为了得到动力系统的全部参数，需提前建立螺旋桨驱动设备模型，用F（ns，M）表示，其含义为动力驱动装置的转速ns和扭矩M与驱动设备的控制量PWM或油门开度TPS，环境参数以及设计特性参数有关。

对于电动驱动装置，

F（ns，M）=f（I，U，Θm，PWM） ，（16）

其中，I、U、Θm、PWM分别表示电流、电压、电机基本参数集以及油门控制量。

对于油动驱动装置，

F（ns，M）=f（P0，T0，Θe，TPS），（17）

其中，P0、T0、Θe、TPS分别表示环境压力、环境温度、发动机基本参数集以及油门控制量。

鉴于篇幅有限，本文利用假设F（ns，M）已知，则可依据图 4所示的计算流程计算得到在多个来流速度下的推力数据曲线。其中图 9所示的油门开度表示螺旋桨在一定来流情况下驱动螺旋桨达到相应转速时电机的控制量或油门开度，其值一般作为油动发动机和永磁无刷电机的控制参量。

将图9所示的系列数据曲线用数学语言表达，即为在约定的来流条件下，每个动力单元的升力Fi或推力Ft与当前的转速和控制变量有关：

Fi=MAPini，PWM，i=1，2，3，4Ft=MAPtnt，TPS，（18）

公式（18）中的ni表示垂直升力单元螺旋桨转速，nt表示推进螺旋桨转速。MAPi、MAPt分别表示升力单元螺旋桨和推进螺旋桨的性能数据组，在Matlab中一般以二维数组的形式被引用。联合公式（2）、公式（6）以及公式（18），将三式归类表示如下：

mV·=∑4i=1Fi+Ft+G+Drag+Fl

Fth=F1F2F3F4FtAijkFi=MAPini，PWM，i=1，2，3，4Ft=MAPtnt，TPS。（19）

公式（19）即为复合翼飞行器完整的动力模型的数学表达，可计算当前飞行条件下的动力需求和驱动设备的控制参量。

5  结论

本文以通识的叶素片条理论建立螺旋桨的力学模型，为估计动力系统的性能鉴定基础。针对叶素理论在实际应用中的难点，本文采用桨前气流速度增量实现快速计算。为精确计算，详细测取螺旋桨的叶素结构数据，引入Profili翼型数据库得到螺旋桨的气动参数，保证数据来源的可靠。另外，利用螺旋桨动量理论的结论和方法优化叶素计算流程，使计算的结果从物理原理上保证准确性。

考虑到本模型做出一定的简化及假设，计算的结果亦说明不能保证模型在螺旋桨全部运行工况的准确性，对此限制模型的使用范围。当J>0.07，模型计算的推力误差小于5%，功率计算误差小于10%，可以用于一般的工程估计。

参考文献：

［1］刘沛清，鲁金华. 涵道螺旋桨气动计算的片条理论及其应用［C］∥第二十二届全国直升机年会.保定：中国航空学会，2006.

［2］刘沛清. 空气螺旋桨理论及其应用［M］. 北京： 北京航空航天大学出版社， 2006.

［3］夏贞锋. 螺旋桨滑流数值模拟方法及气动干扰研究［D］. 西安： 西北工业大学， 2015.

［4］辛冀， 董圣华， 刘毅， 等. 六旋翼无人机的飞行力学建模研究［J］. 飞行力学， 2016， 34（6）： 10-14. DOI： 10.13645/j.cnki.f.d.20160922.001.

［5］杨成顺. 多旋翼飞行器建模与飞行控制技术研究［D］. 南京： 南京航空航天大学， 2013.

［6］徐宝梅. 小型四轴飞行器建模与控制系统设计［D］. 成都： 电子科技大学， 2017.

［7］金伟. 小型双发固定翼无人机飞行控制系统设计［D］. 上海： 上海交通大学， 2019.

［8］莫秋兢. 四旋翼飞行器飞行控制系统算法研究［D］. 广州： 华南理工大学， 2017.

［9］王乐乐. 基于SimMechanics的无人飞行器飞行动力学仿真建模研究［D］. 南京： 南京航空航天大学， 2018.

［10］王春阳， 周洲， 王睿， 等. 涵道式垂直起降固定翼无人机纵向稳定性研究［J］. 西北工业大学学报， 2021， 39（4）： 712-720.

［11］伊朝阳. 共轴双桨飞行器的建模控制与实现［D］. 北京： 北京工业大学， 2017.

［12］冯姣. 基于Web的飞行仿真系统的研究与实现［D］. 绵阳： 西南科技大学， 2020.

［13］聂营， 王生， 杨燕初. 螺旋桨静推力数值模拟与实验对比分析［J］. 计算机仿真， 2009， 26（3）： 103-107. DOI： 10.3969/j.issn.1006-9348.2009.03.027.

［14］裴思宇. 多旋翼电动无人机动力系统建模与旋翼失效性能评估研究［D］. 长春： 吉林大学， 2021.

［15］丁倩岚. 无人机螺旋桨气动性能实验与数值模拟仿真研究［D］. 天津： 天津大学， 2015.

［16］张航， 宋笔锋， 王海峰， 等. 电动固旋翼无人机动力系统建模与优化设计［J］. 航空动力学报， 2019， 34（6）： 1311-1321. DOI： 10.13224/j.cnki.jasp.2019.06.014.

［17］王刚， 胡峪， 宋笔锋， 等. 电动无人机动力系统优化设计及航时评估［J］. 航空动力学报， 2015， 30（8）： 1834-1840. DOI： 10.13224/j.cnki.jasp.2015.08.006.

［18］MCDONALD R A. Electric propulsion modeling for conceptual aircraft design［C］// 52nd aerospace sciences meeting， Maryland，USA： American Institute of Aeronautics and Astronautics（AIAA）， 2014. DOI：10.2514/6.2014-0536.

［19］CORRIGAN IV E K. Survey of small un-manned aerial vehicle electric propulsion system［D］.Dayton： University of Dayton，2007.

［20］GUR O， ROSEN A. Optimizing electric propulsion systems for unmanned aerial vehicles［J］. Journal of Aircraft， 2009， 46（4）： 1340-1353. DOI： 10.2514/1.41027.

［21］LAWRENCE D， MOHSENI K. Efficiency analysis for long duration electric MAVs［C］//Proceedings of the Infotech@Aerospace. Virigina，USA： AIAA， 2005. DOI： 10.2514/6.2005-7090.

［22］陈军， 杨树兴， 莫雳. 电动无人机动力系统建模与实验［J］. 航空动力学报， 2009， 24（6）： 1339-1344.

［23］MAGNUSSEN ， HOVLAND G， OTTESTAD M. Multicopter UAV design optimization［C］//2014 IEEE/ASME 10th international conference on mechatronic and embedded systems and applications （MESA）. Senigallia， Italy：IEEE， 2014： 1-6. DOI： 10.1109/MESA.2014.6935598.

［24］全权.多旋翼飞行器设计与控制［M］.北京：电子工业出版社，2018.