考虑道路限制的建设场地内车辆调度问题研究
李国俭 徐君 吴海军 沈磊 王一夫 李宪利 郑汉坤


DOI:10.3976/j.issn.1002-4026.20230047
收稿日期:2023-03-17
作者简介:李国俭(1977—),男,高级工程师,研究方向为能源电力技术。E-mail:lgjian77@126.com
*通信作者,沈磊,男,工程师,研究方向为新能源发电。E-mail :2733797096@qq.com
摘要:针对大型设备运输车辆进入建设场地后,在场内道路上的车辆调度和路径规划问题进行了研究。受场内道路宽度限制,车辆难以在同一道路上相向行驶;同时,由于不同车辆所运输的货物及运输任务的紧急程度不同,车辆的通行具有不同优先级。针对上述特性,利用时空网络技术构建整数规划模型,在考虑道路限制和不同车辆优先级情况下,对建设场地内的车辆进行调度和会车规避。模型的目标为最小化所有车辆在场内的总时间,包括行驶时间和会车等待时间;模型包含两类约束,即车辆流平衡约束和车辆会车避让约束。为快速有效地求解模型,设计基于时空网络的启发式算法得到各车辆的时空路径,为车辆的路径规划和会车避让提供指导。结合一个实际的大型风电场路网,构建多个算例,对模型和算法的有效性进行验证。结果表明,提出的算法能迅速对不同规模的问题进行求解;另外,算法可以在消除车辆时空冲突的同时,保证车辆在会车时不等待过长时间,最终的方案具有较高的车辆运输效率。
关键词:建设场地;道路限制;车辆调度问题;时空网络;冲突规避
中图分类号:U492.33 文献标志码:A 文章编号:1002-4026(2024)03-0076-09
开放科学(资源服务)标志码(OSID):
The vehicle scheduling problem at a construction
site considering road restrictions
LI Guojian1,XU Jun2,WU Haijun2,SHEN Lei2*,WANG Yifu2,LI Xianli2,ZHENG Hankun3
(1. SPIC Nei Mongol Energy Co., Ltd., Tongliao 028011,China;2. Inner Mongolia Chahar New Energy Co., Ltd.,
Wulanchabu 011800,China; 3. School of Systems Science,Beijing Jiaotong University, Beijing 100044, China)
Abstract∶This study investigates vehicle scheduling and path planning problems on field roads after large equipment transportation vehicles enter construction sites. Due to road width limitations and varying task priorities, vehicles have difficulty traveling in opposite directions on the same road. Furthermore, the large equipment transportation vehicles have different priorities depending on their loads and urgency of the transportation. To address these challenges, this study constructs an integer programming model based on spatiotemporal network technology that minimizes the total travel time of all vehicles on the site by considering road restrictions and vehicle priorities. Furthermore, vehicle flow balance and meeting avoidance constraints are incorporated into the model. Moreover, a heuristic algorithm is designed to efficiently solve the model and obtain the spatiotemporal path of each vehicle, thereby providing guidance for vehicle path planning and passing each other. The effectiveness of the proposed model and algorithm is demonstrated through multiple cases based on an actual wind farm road network. The computational results show that the algorithm can quickly solve the vehicle path planning problem at various scales. Additionally, it can guarantee short waiting time to avoid vehicle meeting while eliminate spatiotemporal conflicts. Moreover, the proposed approach showed high transportation efficiency.
Key words∶construction site; road restriction; vehicle scheduling problem; spatiotemporal network; conflict avoidance
随着社会各类工程建设进程的不断加快,大型设备、构件及物料运输车辆的路径规划逐渐成为热点问题,尤其是在建设场地内的路径规划问题。在建设场地内,由于场内道路宽度有限,往往存在因道路狭窄导致大型货物运输车辆无法正常会车的情况,即场内道路不能满足运输车辆在同一路段上对向行驶会车通过。同时,场内运输车辆作业通常较为繁忙,从优化运输效率、节约运输时间的角度,在场内长距离道路上设置会车点可以保证对向行驶车辆顺利会车通行。但是在车辆会车避让过程中,如果车辆会车调度不合理,则会增加运输车辆的会车等待时间,甚至会造成场内道路拥堵,降低车辆利用率,影响设备及物料配送效率,造成运输人力与物力的浪费,导致运输成本增加。因此,如何对建设场地内大型运输车辆进行更为科学合理的路径规划,并对场内车辆进行调度管理来进行会车避让,是一个具有实际意义的课题。
现有考虑道路限制的大型货物运输车辆路径研究主要集中于为装载大型设备的运输车辆进行远途路径规划,通过综合考虑大型货物公路运输的安全性、经济性、时效性等影响因素,建立其运输路线选择模型[1-4],但未进一步针对运输车辆在受限的场内道路中如何选择运输路径的问题进行探讨。而在针对场内运输车辆路径问题的研究中,大多基于交通仿真技术对场内交通运行情况进行模拟,以达到减少场内交通拥堵和交通事故的目的。郑家祥等[5]应用系统仿真的方法对施工场内交通运输过程进行了仿真研究;刘宁[6]建立了基于土石方调配模型的施工场内交通仿真与优化模型,给出了仿真与优化流程,并将其应用于优化过程中;周思等[7]提出以运距最短为前提,综合考虑各道路行车密度、运输强度、岔口压力以及运输机械的载重量、运行限制等因素,寻求最优的物料运输线路。但大多数研究对象仅涉及大坝工程的施工场内模拟,对场内交通运输的影响因素考虑不充分。同时,大部分现有研究均使用仿真模拟方法来对场内运输车辆路径问题进行研究,缺乏从数学建模的角度来对车辆路径进行系统优化。
时空网络建模方法在车辆路径规划领域有着广泛应用[8],该类模型根据实际路网中的路口节点和路段来构造时空网络的节点和弧,可以更精确地获得离散时间下车辆从出发到驶至客户点途径各节点的时刻,有利于运输车辆的调配。一些学者利用时空网络建模方法,考虑不同现实场景约束的运输车辆路径规划展开了深入研究。Yan等[9]为搬家公司开发了一个优化客户选择和车辆调度的模型,通过构建时空网络模型来描述运输车辆的装卸活动和最大化灵活客户方的选择,并基于分解算法来进行有效求解。Wang等[10]利用时空网络构建了一个两阶段的拾取和交付问题模型。高一鹭等[11]提出了一种基于时空网络的路径优化方法,以解决自动化集装箱码头运输中的路径冲突问题。吴正阳等[12]采用时空网络模型来避免子回路的产生,对车辆配送路线规划问题进行更加直观准确的描述,该模型以扩大模型规模为代价丰富了车辆配送路径选择方案,并求解车辆到达、离开客户点的时刻。以上文献结合货物及物料配送领域中存在的实际应用问题进行研究讨论,利用时空网络方法对具体场景进行准确描述,提高了运输车辆作业调度及路径规划的效率,但未有文献采用时空网络方法来对考虑道路宽度限制的场内运输车辆路径规划问题进行研究。
本文采用时空网络建模方法研究了建设场地内的大型车辆调度问题,在该场景下考虑道路限制造成的车辆会车避让,对场内车辆进行调度及会车引导,从而避免时空冲突。针对研究问题,提出了基于时空网络的场内车辆路径规划模型与算法,优化场内不同种类的运输车辆通过会车点的次序,并对比场内所有运输车辆在时空网络中所占用的弧与对应的离散时间点是否重叠,以此为基础设计算法排开风电场内所有运输车辆在时空网络中的重叠部分,使得所有车辆在场内的总时间最小。
1 问题描述
将建设场地路网抽象为拓扑网络G=S,L,其中,L(l∈L)是拓扑网络中边的集合,S(s∈S)是拓扑网络中的节点集合。节点包括路口节点和会车点,S*为会车点集合。以图1(a)中的实际路网为例,共包括11条原始路段,12个节点。其中原始路段(5, 10)由于距离过长,中途设置了会车点7以方便场内车辆的会车避让,在拓扑网络中将其视为两个路段(5, 7)和(7, 10)。此外,路网中的所有路段均为双向行驶的单车道,在拓扑网络中一条路段可以看作两个有方向的边l和l′,l和l′方向相反组成一个冲突边对l,l′,l和l′不能同时被占用。最后,图1(a)对应的拓扑网络共包括22条边,12个节点。
基于构建的拓扑网络,本文旨在对研究时段内给定的车辆集合进行车辆调度,其中时间维度用离散的时间点来表示,而不同车辆具有不同的优先级,优先级越高的车辆在会车时优先通行,而优先级低的车辆则在会车点进行避让等待。本文使用时空网络技术来直观、具体地反映车辆会车避让的等待时间和时空轨迹。以图1(a)中的车辆1和2为例,图1(b)的时空网络展示了两个车辆的时空轨迹。如图所示,车辆1和2的路径冲突,需对其进行会让指导。考虑车辆1优先级高于车辆2,因此车辆2在时间点5到达会车点7后,需停车等待,直至车辆1驶出路段(5, 7)后才能驶入路段(7, 5)。
2 优化模型
2.1 符号定义
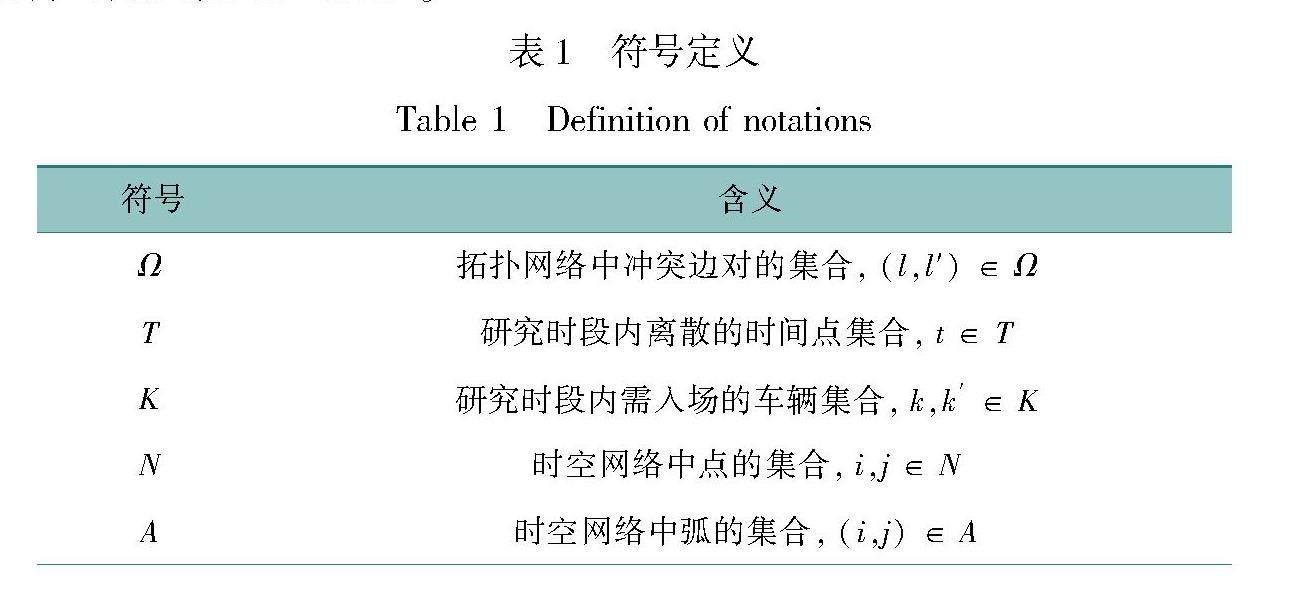
本文涉及的其他符号定义如表1所示。
2.2 时空网络构建
时空网络中的一个点表示拓扑网络上的节点在时间轴上的虚拟拓展点,点的属性包括其对应的拓扑网络中的节点、其对应的离散时间点。则时空网络中点的集合为
N={i|ρ1i=s,ρ2i=t,s∈S,t∈T},(1)
其中,ρ1i为点i对应的拓扑网络中的节点,ρ2i为点i对应的离散时间点。
时空网络中的弧描述了车辆的活动,分为等待弧和行驶弧两种。其中等待弧表示车辆在会车点进行避让的等待活动,只发生在会车点处。等待弧的起终点所对应的拓扑网络中的节点相同,且对应的离散时间点相差1,即
Aw={(i,j)|ρ1i=s,ρ1j=s,ρ2i=t-1,ρ2j=t,s∈S*,t∈T\{1}}。(2)
行驶弧表示车辆在拓扑网络中一条边上的行驶活动,即从边的起始节点行驶至其终点节点。因此,行驶弧是基于拓扑网络中的每条边构建的,行驶弧起终点对应拓扑网络中一条边的起始、终点节点,且起终点对应的离散时间点差值为边的车辆行驶时间,即
Ar={(i,j)|ρ1i=s(l),ρ1j=e(l),ρ2i=t-trunl,ρ2j=t,t∈T\{1,…,trunl},l∈L},(3)
其中拓扑网络中边对应的行驶弧集合为
Arl={(i,j)∈Ar|ρ1i=s(l),ρ1j=e(l),ρ2j-ρ2i=trunl}。(4)
2.3 模型构建
基于上述构建的时空网络,本文构建了相应的场内车辆路径规划模型,设置二元变量xkij(k∈K,(i,j)∈A),其值取1时表示车辆k经过时空网络中的弧(i,j),反之值为0。模型的目标为所有车辆在场内的总加权时间最小,包括等待时间和行驶时间。权重用车辆的优先级来衡量,以此确保优先级低的车在会车时进行避让等待,则目标函数为
min Z=∑k∈K∑(i,j)∈Awqkxkij+∑k∈K∑(i,j)∈Arqkxkij(ρ2j-ρ2i) 。(5)
模型的约束包括两类,即车辆的流平衡约束和车辆会车避让约束。流平衡约束见式(6)~(10)。其中式(6)表示车辆在给定的起点和时间入场;式(8)表示车辆最终到达给定的终点;式(7)和(9)禁止车辆驶回起点和驶出终点,以此来消除车辆路径上的子回路;式(10)表示车辆在其他点上的流平衡约束。
∑(i,j)∈Ar|ρ1i=ok,ρ2i=tdepkxkij=1,k∈K ,(6)
∑(j,i)∈A|ρ1i=ok,ρ2i=tdepkxkji=0,k∈K ,(7)
∑(i,j)∈Ar|ρ1j=dkxkij=1,k∈K ,(8)
∑(j,i)∈A|ρ1j=dkxkji=0,k∈K ,(9)
∑(i,j)∈Axkij=∑(j,i′)∈Axkji′,j∈N,k∈K|ρ1j∈S\{ok,dk} 。(10)
车辆会车避让约束如式(11)所示。对于拓扑网络中的一个冲突边对l,l′来说,式(11)表示当车辆k′经过边l对应的一条行驶弧(i′,j′)时,离散时间点ρ2i′前后Δtpass时间内(即区间[ρ2i′-Δtpass,ρ2i′+Δtpass])没有任何其他车辆驶入路段l。
∑k∈K\{k′}∑(i,j)∈Arl′|ρ2i∈[ρ2i′-Δtpass-trunl′,ρ2j′+Δtpass]xkij≤M(1-xk′i′j′),k′∈K,(l,l′)∈Ω,(i,j)∈Arl 。 (11)
3 求解算法
上述模型旨在为研究时段内的所有车辆分配一条时空路径,每条时空路径上不存在任何时空冲突,目标为最小化场内所有车辆的时间。为了快速求解上述模型,本文考虑根据各车辆给定的起终点,利用Yen算法(偏离路径法)计算得到各车辆的K短路径[13],之后计算得到各车辆到达最短路径上各节点和占用各路段的时间信息。若车辆间存在时空冲突,根据冲突车辆优先级属性,首先遍历寻找优先级低的车辆K段路径集合中未被优先级高的车辆占用的K短路,若存在该条路径,则安排优先级低的车辆更改当前路径,按照所搜索到的K短路行驶;若不存在该条路径,则安排优先级低的车辆在会车点等待直到优先级高的车辆离开冲突路段。特别地,当两个车优先级相同时,根据先到先服务原则,优先让入场时间早的车辆进入冲突路段。根据冲突的预计发生时间,解决当前最早发生的冲突,直到场内所有运输车辆都有无冲突的路径。
对于轨迹时空冲突较少的情况,算法迭代较少的次数就可以得到所有车辆间无冲突的时空路径。但当多个车辆聚集在路网中的某一区域时,可能会产生拥堵现象。此时,若在调整车辆行驶路径时没有考虑后续影响,冲突路段的前1个节点的等待或路径重新调整可能会导致车辆轨迹的二次冲突。为了解决上述车辆二次冲突和多个车辆在同一路段存在会车冲突的问题,本文提出了一种基于时空网络的冲突解决方法,如图2所示。假定需要规划运输车辆C在t时刻经过n个时间刻度到达D的路径,若在时空网络中不存在Ct到Dt+n的通路(路径中的弧和点被其他运输车辆占用),此时C需在到达Dt+n前在会车点处等待wt直至拥堵消除,此时运输车辆C到达的时间网络节点更新为Dt+n+wt。
算法的主要流程如下:
步骤1 第1辆车进入路网,编号i=1,使用Dijkstra算法计算车辆1行驶的最短路径,记录车辆1最短路段集合{[Sp,Sq]},经过路段时间段集合{[aSp1,dSq1]},其中aSp1=Gs0spc,dSq1=Gs0sqv,Gs0sp是从起点SO到Sp的距离,c是车速。
步骤2 每有后续新车进入路网,i=i+1,若i>I进入步骤5,否则初始化K短路集Pi,候选集Xi,确定起点si,终点ti,松弛系数δ(K短路径的长度与最短路径的长度的比值),使用Dijkstra算法计算车辆i行驶的最短路径pi1,pi1放入集合Pi中,计算pi1的长度fpi1,令F=δ×fpi1,令k=1,记录pi1路段集合{[Sp,Sq]}和路段时间段集合{[aSpi,dSqi]},其中aSpm=Gs0spc,dSqm=Gs0sqc。
步骤3 若k>K,进入步骤2,否则从pik中最靠近t的点开始到点si,点v摆动到所有可能连接的点m上,vm满足不在候选集Xi的条件。使用Dijkstra法搜索点m到ti的最短路,记为pm,把pksv、vm和pm组成的偏离径路放入候选集Xi中,其中pksv表示pik上从si到v的子路径。
步骤4 若候选集Xi为空,进入步骤2;若不为空,计算所有候选集中路径fp升序排列,最小值路径记为pik+1,只保留前K条路径,若fpik+1>F进入步骤5,否则把pik+1移入Pi中,k=k+1,进入步骤3。
步骤5 对场内所有车辆所经过的路段队列和所经过路段的占用时间队列进行两两比较,若存在两辆车行驶方向相反、所经过占用时间有冲突的路段,则提取出其中最先发生的路段Si,Sj,同时记录两辆车经过上述路段时各自的占用时间aSim,dSjm,判定两个车辆会在场内行驶途中发生会车冲突,此时进入步骤6比较两个车辆的优先级Pm,Pn;若不存在占用时间重合的路段Si,Sj,则车辆按照初始最短路径时空信息行驶。
步骤6 对比场上车辆优先级属性值,设优先级高的车辆为m1,优先级低的车辆为m2。按照所述车辆会车避让准则对两个车辆进行会车指导,首先遍历车辆m2的K短路集合,判断是否存在未被优先级更高的车辆占用的次短路,计算该路径上的总行程时间tk。若存在,则令车辆m2按此次短路径行驶,更新车辆m2经过路段{[Sp,Sq]}及时间段集合{[aspm2,dsqm2]}。若不存在,接着遍历优先级低的车从入口到冲突路段之间的路口,若存在会车点,则令车辆在会车点处等待,更新车辆m2经过路段{[Sp,Sq]}及时间段集合{[aspm2,dsqm2]};若不存在会车点,则令车辆m2在车辆入口等待,等待时间w=dsjm1-asjm2,并重新计算此时车辆行驶最短路总行程时间t,其中aspm2=aspm2+w,dsqm2=dsqm2+w,p,q≥i,j。更新避让车辆路径信息,并返回步骤5。
步骤7 对比场内所有车辆所经过路段队列和经过路段的占用时间队列无重合部分终止。
4 算例分析
为了验证提出的模型和求解算法的有效性,本文以一个实际的大型风电场的场内路网为例,构造案例进行求解分析。算法使用Python编程实现,在2.20 GHz PC,16 GB RAM,Windows11,64位操作系统上运行。
4.1 小规模算例
所研究的风电场场内路网如图3所示,我们将路网中的路口节点分为一般节点、在场区边界的出入口以及卸货点。在图3中,F为会车点,M为场区边界的出入口,D为卸货点,S为一般路口节点。在这部分的小规模算例中,我们仅考虑3辆车,车辆的起终点、入场时间、优先级等信息如表2所示。由表可见,车辆1和车辆3的优先级低于车辆2。
采用所提出的算法对该算例进行求解。首先得到各车辆从任务起点至终点的初始K(K=5)短路径集合,然后计算得到车辆经过路网各节点的时刻,对比计算第k短路上的车辆行驶时间和当前最短路径上的行驶时间,进行多次迭代循环。当k=1时,得到无冲突的车辆时空路径,即取当前所规划的最短路径。最终结果中,3辆车间的时空冲突都得到消除,冲突数量达到0。表3展示了最后各车辆的时空路径结果,而图4展示了各车辆会车避让调整前后的时空路径。从结果图表中可以看出,车辆1为避让会车优先级更高的车辆2,在会车点F8处等待了1.7 min,待车辆2通过冲突路段后,车辆1继续行驶;而对于车辆1和车辆3产生的会车冲突,由于车辆1和车辆3会车优先级相同但车辆1作业时间更早,所以此时由车辆3在会车点F7处停车等待。最后,车辆2在场内无须等待,车辆1和车辆3在场内的等待时间与场内总时间的比值分别为3.64%和8.01%。
4.2 大规模算例
在相同的路网上,这部分构建了不同车辆规模的大规模算例,并对结果进行对比分析。共做了4组实验,车辆数分别为20、40、60、80,随机生成车辆的起点、终点、优先级和出发时间等信息。
使用本文提出的求解算法对模型进行求解,算法运行时间会随车队规模增加而增大,并且计算时间均在
1 s以内。图5展示了4组实验下的对比统计结果,包括无需等待车辆数、车辆平均等待时间和平均运行时间。显然,无需等待车辆数随着车队规模增大而增加,但是其占总车辆数的比例随着车队规模增大而减小。这是因为车队规模越大,车辆间的时空冲突越多,需要会车等待的车辆比例越高。图5中红色折线代表车辆平均等待时间,蓝色折线代表车辆平均运行时间。由图6可以看出,当车队规模为20时,车辆平均等待时间和平均运行时间最小;当车队规模≥40时,车辆平均等待时间和平均运行时间基本保持不变。由此可见,车队规模对车辆平均等待时间和平均运行时间影响很小。
图6展示了不同车队规模下路网上所有车辆为进入各路段的总等待时间分布情况,用于挖掘路网上的瓶颈路段,即路网上最容易发生车辆冲突和等待的路段。从图6中可以看出,随着车队规模的增大,出现车辆冲突的路段数量随之增加,而所有冲突路段上的总等待时间也不断增长。该现象说明场内车辆数量越多,路网上的拥堵程度越严重。而当车队规模达到40辆及以上时,F8-D6路段上的车辆总等待时间显著高于其他路段,且在不同车队规模增场景下均高于其他路段。因此在实际应用中,当场内车辆较多时,可考虑拓宽F8-D6路段或采取其他相关措施,对该路段进行拥堵疏解来减少场内车辆间的冲突和等待时间。
此外,场内车辆总等待时间占总行驶时间的百分比可有效反映车辆的运输效率,该值百分比越高,则说明车辆在行驶全程耗费的等待时间越多,运输效率越低。如图7所示,随着车队规模的增加,上述百分比指标不断上升,可知场内车辆数量增加时会造成车辆运输效率降低。而当车队规模超过40辆时,该指标上升趋势明显放缓,由此可见本文中提出的算法可在车辆较多时有效安排车辆合理避让,尽可能减少等待时间在总行驶时间中的占比,具有较强的实际应用性。
5 结论
针对建设场内运输车辆在道路限制的场景下面临的对向会车冲突问题,基于时空网络模型提出了一种求解算法,来规避车辆间的时空冲突。时空网络模型以最小化车辆在场内总时间为目标,算法利用时空网络的特性进行模型刻画,通过时空对比计算出冲突产生的位置和时间,并通过调节车辆在会车点的等待时间排除冲突。另外,以一个大型风电场的实际路网为基础构造多个算例验证提出的模型和算法的有效性。通过对比分析可得:
(1)所提出的模型可兼顾场内所有车辆的时空分布信息,为每辆车辆提供导航指令,在车辆行驶冲突产生之前进行规避,有效消除车辆间的行驶冲突,具有较强实际应用性;
(2)提出的算法效率很高,在算例中的不同车辆规模下都能在1 s内得到结果,能满足实时要求,可以很好地应用至实际车辆导航中。
(3)提出的模型和算法,在不同车辆规模下均可在消除车辆间行驶冲突的同时,保证车辆在会车时不等待过长时间,最终的方案具有较高的车辆运输效率。
参考文献:
[1]RAY J J. A web-based spatial decision support system optimizes routes for oversize/overweight vehicles in Delaware[J]. Decision Support Systems, 2007, 43(4): 1171-1185. DOI: 10.1016/j.dss.2005.07.007.
[2]OSEGUEDA R, GARCIA-DIAZ A, ASHUR S, et al. GIS-based network routing procedures for overweight and oversized vehicles[J]. Journal of Transportation Engineering, 1999, 125(4): 324-331. DOI: 10.1061/(asce)0733-947x(1999)125: 4(324).
[3]申世杰. 大件产品公路运输安全管理系统研究及应用[D]. 重庆: 重庆大学, 2008.
[4]吴丽丽. 重大件公路运输若干问题的研究[D]. 哈尔滨: 东北林业大学, 2007.
[5]郑家祥, 殷奎生. 高土石坝施工过程计算机模拟[J]. 水电站设计, 1993, 9(2): 70-75.
[6]刘宁. 高心墙堆石坝施工场内交通仿真与实时控制研究[D]. 天津: 天津大学, 2013.
[7]周思, 肖宜, 申明亮, 等. 大型水利工程土石方调配道路系统建模研究[J]. 中国农村水利水电, 2011(5): 109-112.
[8]WANG Y, ZHANG S L, GUAN X Y, et al. Cooperation and profit allocation for two-echelon logistics pickup and delivery problems with state-space-time networks[J]. Applied Soft Computing, 2021, 109: 107528. DOI: 10.1016/j.asoc.2021.107528.
[9]YAN S Y, CHU J C, HUNG W C. A customer selection and vehicle scheduling model for moving companies[J]. Transportation Letters, 2020, 12(9): 613-622. DOI: 10.1080/19427867.2019.1671061.
[10]WANG L F, SONG J, SHI L Y. Dynamic emergency logistics planning: models and heuristic algorithm[J]. Optimization Letters, 2015, 9(8): 1533-1552. DOI: 10.1007/s11590-015-0853-z.
[11]高一鹭, 胡志华. 基于时空网络的自动化集装箱码头自动化导引车路径规划[J]. 计算机应用, 2020, 40(7): 2155-2163. DOI: 10.11772/j.issn.1001-9081.2019122117.
[12]吴正阳, 鲁工圆, 马驷. 多资源约束下车辆配送路径优化模型[J]. 交通运输工程与信息学报, 2018, 16(1): 122-130. DOI: 10.3969/j.issn.1672-4747.2018.01.019.

