核心素养下的初中数学教学策略分析

刘汉平

【摘要】文章以让初中生通过数学课程的学习，形成会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界的数学学习品格与关键能力为目标，以“生活即教育、社会即学校、教学做合一”为指导思想，结合在初中数学课堂教学中培养学生学科核心素养的策略，做出了密切联系苏科版初中数学教材内容的案例分析，旨在持续增强初中数学教育的育人水平和教学质量，贯彻落实促进学生实现数学“三会”的新课标理念.

【关键词】核心素养；初中数学；教学策略；“生活即教育”；“社会即学校”；“教学做合一”

【基金项目】本文系江苏省徐州市“十四五”规划课题《数学课程核心素养视野下课堂教学转型的行动研究》（课题编号：GH14-21-L020）的阶段性研究成果.

《义务教育数学课程标准（2022年版）》（简称“新课标”）概括归纳了义务教育阶段学生在数学学习过程中，所形成的数学核心素养，且明确指出，“义务教育数学课程应使学生通过数学的学习，形成和发展面向未来社会和个人发展所需要的核心素养”“实现义务教育阶段的培养目标，使得人人都能获得良好的数学教育”.由此可见，在初中阶段的数学课程教学中，要加强加大对学生数学核心素养培养的必要性及关键性.下面笔者在把握初中生数学眼光、数学思维及数学语言形成发展特点的基础上，对在数学课堂教学中运用生活教育理论培养学生学科核心素养的策略方法做出说明.

一、生活即教育，联系生活创设情境，用数学眼光观察现实

会用数学的眼光观察现实世界，是初中生在数学课程学习中形成抽象能力、几何直观、空间观念及创新意识的集中体现.这是一种从数学的角度，认识与探究现实世界客观现象中所蕴含的数量关系与空间形式，并提出有意义的数学问题的数学核心素养和数学学习能力.初中数学教师在应用陶行知生活教育理论培养学生数学眼光时，可以教学情境为载体，将学生在实际生活中常见的现象转移到课堂中来，为学生创设直观形象、真实立体的数学教学情境，以此活跃数学课堂教学氛围，启发引导学生进行数学抽象，促使学生逐步形成从数学角度观察现实世界的意识习惯，进而发展其好奇心、想象力与创新能力.

例如，在苏科版七年级下册数学教材“二元一次方程组”一课中，引导学生认识二元一次方程组时，初中数学教师就可以从“生活即教育”的角度为学生创设数学教学情境，促使学生用数学的眼光观察现实世界与实际生活.

首先，初中数学教师可以联系学生的小学数学生活，让学生从方程的角度再度分析与思考经典数学问题———鸡兔同笼：“今有鸡兔同笼，上有三十五头，下有九十四足，问鸡兔各几何.”并利用微课教学技术，为学生播放与鸡兔同笼有关的动画，以调动学生的多重感官与数学学习兴趣，促使学生自觉类比已知的二元一次方程知识，列出两个方程，即设鸡有x只，兔有y只，便能得到两个关于未知数x与y的方程：x+y=35，2x+4y=94.随后，初中数学教师可将联立两个方程求解未知数的过程呈现给学生，让学生认识到将含有两个未知数的两个一次方程联立在一起组成的方程组，就是二元一次方程组.

最后，初中数学教师可引导学生求出方程组的解，促进学生的数学探究与分析能力的发展.由此，初中生就会在兴趣的内驱作用下，更为积极踊跃地参与解二元一次方程组的数学学习活动中，这不但能够让学生清楚地体会到二元一次方程组的解是二元一次方程组中两个方程的公共解，同时能够让学生由衷地感受到应用二元一次方程组解决现实生活问题、形象刻画现实世界中客观事物数量关系的实际意义，从而达到促进学生数学学习方式变革与数学眼光发展的教学目的.

二、社会即学校，联系生活提炼问题，用数学思维理解现实

会用数学的思维思考现实世界，是中学生在数学学习过程中发展运算能力、推理意识与推理能力的主要表现.数学是一门逻辑性、结构性与抽象性较突出的基础课程，在学习数学、分析解决数学问题与应用数学思想方法的过程中，初中生将经历独立的数学思维过程，主动建立起数学对象之间、数学与现实世界之间的逻辑联系，从而逐步形成重逻辑、有条理的理性思维和科学态度.基于陶行知生活教育理论，实施与展开培养初中生数学思维的数学教育工作时，初中数学教师可以充分借助问题导学法的思维引领作用及优势，向学生提出与现实世界、社会生活有密切关联的具有启发性或引导性的教学问题，启迪学生主动地从数学学科的视角分析思考实际问题，并运用数学学科思维方式和思想方法解决处理生活问题，让学生在感知与体悟数学应用价值的过程中，亲身经历数学的再发现与再生成，从而有效改善思维定式问题，进阶思维能力.

例如，在苏科版八年级上册数学教材“勾股定理”一课中，教师在引导学生推导与证明勾股定理（直角三角形的两条直角边的平方和等于斜边的平方）时，可以让学生仔细观察手中的两种三角板数学学具，并鼓励学生迁移运用已知的三角形认识经验，说出两种三角板数学学具的三角形名称，指出它们的直角边和斜边.

在这之后，初中数学教师可以此为素材，向学生提出具有启发性与引导性的教学问题：“在不等边直角三角板中，两个直角边的长度分别是多少？斜边长度是多少？斜边和两个直角边的数量关系是怎样的？在等腰直角三角板中，两个直角边与斜边的长度是否蕴含同样的数学规律？”以此将学生的注意力更多地集中在对两个三角板边的特征的观察、分析与比较上，然后引导学生以验证勾股定理的真伪为出发点，围绕数学学具展开数学推理、抽象和证明，进而使其通过数学运算，得出“在直角三角形中，斜边的平方等于两个直角边平方之和”的数学结论，充分把握勾股定理的实质.

在学生通过细致研究两种不同类型的直角三角板推导出勾股定理后，初中数学教师还可为学生布置有关勾股定理逆推导、勾股定理实际应用的数学随堂练习题：

【练习一】如图（图2），AD⊥BC，垂足为点D.如果在△ABC中，有CD=1，AD=2，BD=4.那么能否证明△ABC是直角三角形？

【练习二】装修工人欲将一个长为1.8m，宽为0.9m，厚为0.3m的床垫放进长、宽、高分别是1.2m，1m，2m的电梯中，那么这个床垫能放进去吗？为什么？

【练习三】以Rt△ABC三边为边长，绘制三个正方形，并分析三个正方形面积的关系.

通过对手中三角板数学学具三边特征的细致观察及对其中所蕴含数学规律的探究，初中生不但能够充分掌握勾股定理的实质，深刻认识到在直角三角形中，斜边的平方等于两直角边平方之和的数学定理，还能够形成积极用数学的思维思考探究现实世界中客观事物的探究能力，这样其在围绕勾股定理展开数学随堂练习时，也会在无意间实现对勾股定理的逆推导和实际运用，从而学会融会贯通的数学学习方法，学会从更为多元与发散的角度思考、观察及分析现实生活中客观事物及现象中所包含的数学原理和数学规律.如此，初中生的数学问题意识和数学思维能力便会在潜移默化中得以有机形成和稳定提高.

三、教学做合一：联系生活组织实践，用数学语言表达现实

会用数学语言表达现实世界，是学生在学习初中数学课程内容后形成数据观念、模型观念和应用意识的认知表现.数学既是推理和运算的工具，也是表达与交流的语言.由此可见，数学具有与语文学科等同的工具性与人文性统一的特点，能够为学生解释说明现实生活中客观事物的关系、性质与规律提供载体与抓手.基于这一认识，初中数学教师在数学课堂教学中立足陶行知生活教育理论，对学生的数学语言进行针对性培养与集中锻炼时，就可以通过组织学生展开综合性数学实践活动的方式，驱动学生应用数学去表达、解释与分析现实世界的客观事物与现象，以此深化学生对数学语言简洁、优美与精练特点的认识，培养学生应用学科知识的意识和实践能力.

例如，在苏科版九年级下册数学教材“相似三角形的性质”一课教学中，基于陶行知生活教育理论中的“教学做合一”观点培养学生数学语言时，初中数学教师可以在学生基本把握与理解认识相似三角形的性质后，依据学生的数学学习水平与数学问题解决能力均衡划分数学学习小组，并在此基础上，联系物理学科、地理学科与现实生活，为学生布置如下相似三角形性质应用实践和迁移创新的数学学习课题：

【课题1】用相似三角形知识解决物理实验问题.在一次探究小孔成像原理的物理光学实验中，一实验小组观察到燃烧的蜡烛AB经过小孔O在光屏上所成的像A′B′.通过测量，已知蜡烛AB长为35cm，小孔O到蜡烛AB、到像A′B′的距离分别是38cm和24cm，那么像A′B′的长是多少？

【课题2】用相似三角形知识解决地理识图问题.观察中国地图，连接北京、西安、南京三座城市，可将其近似看作等边三角形.通过在比例尺为1∶500的地图上，测量北京到西安、西安到南京、南京到北京的直线距离分别是12cm，10cm与11cm，那么北京到西安、西安到南京、南京到北京的实际直线距离是多少？由三座城市围成的三角形的面积实际是多少？

【课题3】用相似三角形知识解决测高问题.小明在学习光的反射规律后，想到了一个测量未知建筑物高度的方法：在地面点O处（图3）平放一面平面镜，并在平面镜上做标记.然后向后退去，直至在点C处恰好看到未知高度建筑物AB的顶点A在平面镜中的像，且与平面镜上的标记重合.根据人眼到地面的距离、建筑物AB的底端点B到点O、点O到点C的距离，再利用相似三角形性质求出建筑物AB的高度.试判断小明这一测高方法是否能够准确测出建筑物AB的高度.除了这种测高方法外，你们还能想到哪些测量未知建筑物高度的方法？请以校园中的旗杆为研究对象，检验方法并测量旗杆高度.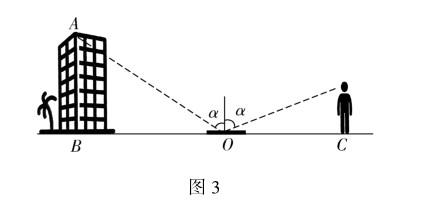

设计【课题1】的目的是让学生能够应用相似三角形的基本性质与数形结合思想方法，进行数学抽象与数学建模，进而准确测量与计算出像A′B′的长度，认识到数学与物理间的紧密关联，形成数理融合的学习意识与数学应用意识.设计【课题2】的目的是让学生能够将数学中的几何图形知识迁移类比到地理学科的地图观察和识别之中，认识与体悟到数学的工具性与应用性.设计【课题3】的目的是让学生能够在验证用光的反射规律测高的方法的正确性后，另辟新径提出更多应用相似三角形性质解决生活中测高问题的技巧方法，从而锻炼学生的创新实践能力.在这一过程中，学生不仅能够实现对已掌握、已习得的相似三角形知识的迁移运用与创新实践，而且能够对数学课程的工具性、实用性和应用性形成更为透彻与深刻的感知体悟，进而发展并形成数学应用意识和数学问题解决能力.

结 语

综上所述，初中生的数学核心素养是在合理运用数学眼光观察现实世界，合理运用数学思维思考现实世界与合理运用数学语言表达现实世界中，不断形成与发展的.在核心素养视域下的初中数学课堂教学中，教师可立足数学课程源于对现实世界抽象的本质，积极关联陶行知生活教育理念为学生创设真实数学情境，向学生提出真实数学问题，引导学生展开综合实践，以此引领数学教育回归生活教育本真，最终实现让学数学核心素养协调发展的育人目标.

【参考文献】

[1]庞平统.初中数学教学现状分析与课堂教学策略研究[J].考试周刊，2022（52）：84-87.

[2]余锦锋.基于核心素养的初中数学课堂教学策略[J].读写算，2022（36）：90-92.

[3]张玉华.基于核心素养的初中数学教学探究[J].数学学习与研究，2022（36）：125-127.

[4]苏雪云，刘艳茹，斯琴其木格.初中数学合作学习教学模式实施策略探讨[J].赤峰学院学报（自然科学版），2022，38（12）：88-92.

[5]张玲.基于学生核心素养发展的初中数学课堂教学分析：以“圆周角的定理”教学为例[J].数学之友，2022，36（24）：28-30.