考虑桩土变形协调的复合地基设计方法

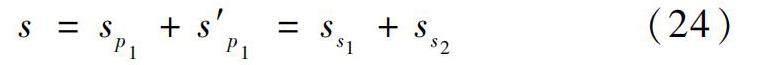
摘要：目前在复合地基的设计中，由于采用桩体压缩模量计算得到的复合压缩模量偏大，造成复合地基加固区沉降被低估；另外桩和桩间土承载力发挥系数取值主观性较强，导致复合地基承载力计算结果偏大。针对上述两个问题，从复合地基形成机理出发，指出桩及桩间土共同直接承担荷载时必须保证桩土变形协调。桩土变形协调的条件是：① 桩刺入垫层的深度不能超过垫层厚度；② 桩宜设置为摩擦桩。在此前提下，分别计算桩及桩间土的沉降，利用桩土变形协调方法得到了桩土应力比和承载力发挥系数理论值，进而得到加固区的沉降计算方法。工程算例证实，从保证复合地基有效设计和工程安全的角度出发，应该根据桩土变形协调来进行复合地基设计计算。

关 键 词：复合地基；桩土变形协调；承载力发挥系数；桩土应力比；沉降

中图法分类号：TU472

文献标志码：A

DOI：10.16232/j.cnki.1001-4179.2024.05.021

0 引 言

近年来，竖向增强体复合地基在国内得到了广泛的应用，作为一种新的地基处理技术，有关规范对复合地基沉降和承载力计算这两个关键问题给出了初步解决方案。譬如复合地基沉降计算，规范［1-3］均采用分层总和法^［4］，将加固区视为一复合地基。对于复合压缩模量，规范［1-2］按照面积加权平均得到；规范［3］是将天然地基的压缩模量乘以承载力特征值增大系数得到。但闫明礼等^［5］认为规范［1-2］对于桩的模量采用桩体压缩模量，会使得到的复合压缩模量计算值偏大，导致加固区复合地基变形计算值偏小；而杨光华等^［6］认为按照规范［3］得到的复合压缩模量偏小，造成加固区变形计算值偏大。刘吉福等^［7］根据桩土作用计算桩土附加应力，然后采用分层总和法计算复合地基沉降，按土层厚度加权平均得到桩间土的平均压缩模量，进而得到桩土模量比，桩土应力比等于桩土模量比的桩段为桩身等沉区。刘彬^［8］针对长短桩布桩方式，对复合地基沉降开展了离散元仿真模拟研究和现场检测分析，提出了采用分离式布桩和交叉式布桩的长短桩复合地基加固方案。李强等^［9］通过现场监测发现，当地基受到荷载后，灌注桩存在向垫层方向刺入的现象。

上述研究表明，采用复合压缩模量进行加固区沉降计算，关键在于桩体模量的合理选用。能够采用桩体压缩模量来计算复合压缩模量的前提是桩只发生压缩变形，而不发生位移^［10］。但实际工程中，桩往往会产生顶部刺入垫层或者底部刺入非加固区土层的位移，使得采用桩体压缩模量来计算复合压缩模量的前提不复存在。

其次，复合地基的承载力计算涉及到桩和桩间土各自承载力特征值的发挥程度（承载力发挥系数）。规范对这些发挥系数给出了经验值，但存在较强的主观性^［1-2］。周同和等^［11］根据某工程场地多桩型复合地基的现场试验，探讨了多桩型复合地基增强体中单桩与桩间土承载力系数的影响因素。王明山等^［12］认为承载力系数如何取值是多桩型复合地基设计计算中的重要问题，并结合工程实例分析了多桩型复合地基的桩土应力比、荷载分担比、桩与土承载力发挥等。上述研究表明，要想较为准确地确定承载力发挥系数，并用来计算复合地基承载力，需要通过现场试验，但即便这样，由于现场试验面积与实际工程处理面积存在尺寸效应，现场小尺寸试验获得的发挥系数与实际工程之间存在差距，有时差距还很大，造成计算结果与实际情况不太相符。

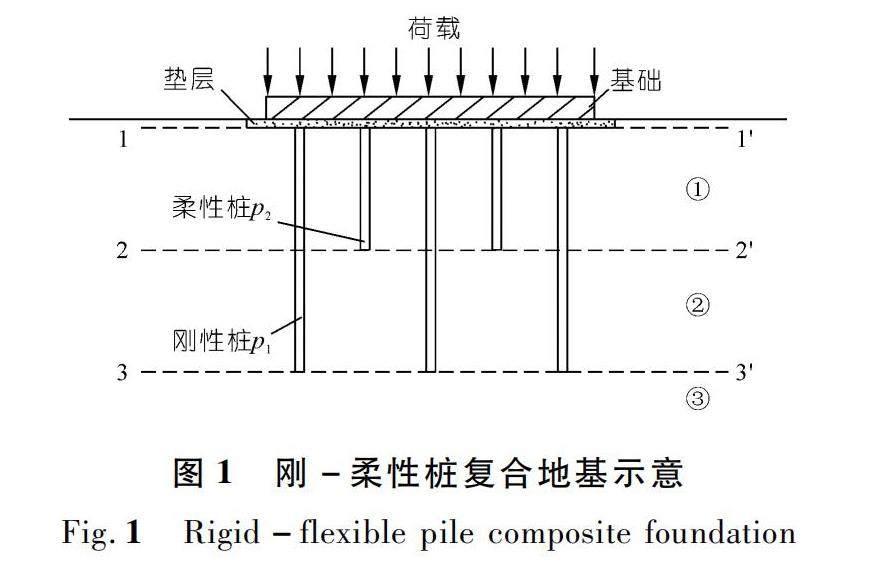
为了解决上述问题，本文以刚-柔性桩复合地基为代表（图1），不再采用复合压缩模量来计算加固区沉降，而是分别计算桩及桩间土的沉降，利用桩土变形协调方法来得到桩土应力比和承载力发挥系数，进而得到加固区的沉降计算值；同时，利用上述方法得到的承载力发挥系数，去解决目前复合地基承载力确定中由于承载力发挥系数取值经验性较强而导致的计算结果主观性偏大问题。

1 桩土变形协调的条件

复合地基与浅基础和桩基础最本质的区别在于复合地基中桩及桩间土共同直接承担上部荷载^［13］。这就必须保证桩土变形协调，否则一旦荷载全部由地基土承担或者由桩承担，复合地基就可能退化为浅基础或桩基础，并极易出现复合地基破坏。要想保证桩土变形协调，必须满足以下两个条件。

（1） 刚性桩刺入垫层的深度不能超过垫层厚度。在刚性基础（如水闸混凝土底板）下的复合地基上设置柔性垫层，可以增加桩间土承担荷载的比例，充分利用桩间土的承载潜能，提高地基承载力。同样地，在柔性基础（如填土路堤和柔性面层堆场）下的复合地基上铺设刚度相对较大的垫层，可以提高桩土应力比，充分发挥桩体的承载潜能，提高复合地基的承载力，减小复合地基的沉降。上述分析表明，垫层在协调桩土荷载分担比例和变形协调这2个方面至关重要。

当垫层设计的较薄时，如果刚性桩设置为端承桩，在上部荷载作用下刚性桩可能向上刺穿垫层，直接顶托刚性基础（如混凝土底板）。此时，由于桩间土压缩变形远大于桩的变形，会使刚性基础与天然地面脱离，上部荷载全部由刚性桩承担，刚性桩承载力发挥系数最大，为1.0；柔性桩和桩间土承载力发挥系数最小，为0，刚-柔性桩复合地基退化为传统意义上的桩基础。由于柔性桩和桩间土不再参与提供承载力，此时利用复合地基承载力计算方法所得结果偏于危险，工程偏于不安全。因此，刚性桩向上刺入垫层的深度s_p1不能超过垫层厚度d，否则复合地基不能形成（图2）。

与刚性桩相比，柔性桩的变形模量小得多，如果垫层采用砂碎石，那么对于刚性基础来说，刚性桩、柔性桩以及桩间土承载力发挥系数从大到小为β₁>β₂>β₃，刚性桩桩顶所受压力大于柔性桩桩顶压力；如果刚性桩和柔性桩桩身半径相等，那么刚性桩刺入垫层的深度要大于柔性桩。因此，柔性桩刺入垫层的深度不会超过刚性桩，柔性桩顶托刚性基础的情况不会发生。

根据上述分析，为了保证刚性桩、柔性桩以及桩间土共同直接承担上部荷载，形成复合地基，需要保证刚性桩向上刺入垫层的深度不超过垫层的厚度，即s_p1≤d，这是刚-柔性桩复合地基垫层厚度设计的基本原理，也是保证刚性桩、柔性桩以及桩间土变形协调的基本条件。对于只有一种竖向增强体的复合地基，如水泥土搅拌桩复合地基，其垫层厚度设计原理与此相同。

需要指出的是，由于刚性桩刺入垫层，在垫层下一定范围的地基土体会在刚性桩桩周对桩产生一个向下的拉力作用，即负摩阻力作用，从而减小刚性桩桩顶刺入垫层的深度，设计时可以相应减小垫层设计厚度。由于该值较小，而且对刚性桩刺入垫层的深度起抑制作用，从垫层厚度设计安全角度出发，可以不计入其影响。

（2） 刚性桩和柔性桩宜设置为摩擦桩。根据上述分析，对于深厚淤泥质地基，宜将刚性桩和柔性桩均设置为摩擦桩，这样桩在上部荷载作用下可以自由移动，形成桩土能够变形协调的有利条件。如果桩设置为端承桩，那么由于桩底位移受阻而迫使桩顶刺入垫层的深度达到垫层厚度的可能性大大增加，很难保证桩在全过程工作中与桩间土始终形成复合地基。

2 复合地基加固区沉降计算

对于深厚软土地基，刚-柔性桩桩端持力层土质均较差，考虑将刚性桩、柔性桩均设置为摩擦型桩，桩顶所受压力全部由桩周土提供的侧摩阻力承担，桩端压力为0。根据图1和图3，对复合地基中刚性桩、柔性桩和桩间土进行应力变形分析。

考虑桩土竖向静力平衡，有：

N_p1Q_p1+N_p2Q_p2+Q_s1=F（1）

式中：N_p1、N_p2分别为刚性桩、柔性桩根数；Q_p1、Q_p2、Q_s1分别为每根刚性桩、每根柔性桩、地基表面各自分担的荷载、F为总荷载。

Q_p1=σ_p11A_p1=β₁f_p1A_p1=n₁₁β₃f_s1A_p1（2）

Q_p2=σ_p21A_p2=β₂f_p2A_p2=n₂₁β₃f_s1A_p2（3）

Q_s1=σ_s1A_s=β₃f_s1A_s（4）

n₁₁=σ_p11/σ_s1=β₁f_p1/β₃f_s1（5）

n₂₁=σ_p21/σ_s1=β₂f_p2/β₃f_s1（6）

n₁₂=σ_p12/σ_s2=β₁f_p1/β₃f_s2（7）

式中：σ_p11、σ_p21分别为刚性桩、柔性桩桩顶处应力；σ_p12为刚性桩在加固区②顶面2-2′处桩的应力；σ_s1、σ_s2、σ_s3分别为加固区①顶面1-1′处、加固区②顶面2-2′处和非加固区③顶面3-3′处地基应力；f_p1、f_p2、f_s1、f_s2分别为刚性桩p₁、柔性桩p₂、加固区①桩间土和加固区②桩间土的承载力特征值；A_p1、A_p2、A_s分别为每根刚性桩、每根柔性桩和桩间土面积；n₁₁、n₂₁为加固区①顶面1-1′处刚性桩和柔性桩桩顶与桩间土的应力比；n₁₂为加固区②顶面2-2′处刚性桩与桩间土的应力比；β₁、β₂、β₃分别为刚性桩、柔性桩以及桩间土地基承载力发挥系数。

将公式（2）～（4）代入公式（1），有：

β₃f_s1（N_p1n₁₁A_p1+N_p2n₂₁A_p2+A_s）=F（8）

设地基处理总面积为A，则根据刚性桩、柔性桩面积置换率m₁、m₂，有：

β₃f_s1A［1+m₁（n₁₁-1）+m₂（n₂₁-1）］=F（9）

m₁=N_p1A_p1/A（10）

m₂=N_p2A_p2/A（11）

对于刚性桩和柔性桩，由于考虑其均为理想摩擦型桩，其桩顶承担的上部荷载全部由各自桩侧土体侧摩阻力承担，桩端压力为0，不向下刺入，其变形只有向上刺入垫层的刺入量和桩身压缩量。刚性桩和柔性桩刺入垫层的刺入量s_p1、s_p2^［14］和桩身压缩量s′_p1、s′_p2分别为

式中：E_d、ν_d分别为垫层的变形模量和泊松比；r₁、r₂分别为刚性桩和柔性桩桩身半径；l₁、l₂为加固区①和②的厚度；E_p1、E_p2分别为刚性桩和柔性桩的桩体压缩模量。

对于加固区①和加固区②来说，桩间土的压缩量分别为

式中：E_s1、E_s2分别为加固区①和②地基土压缩模量；η₁、η₂分别为地基表面1-1′处桩间土应力β₃f_s1在2-2′和3-3′界面处的应力扩散系数，按以下公式计算：

式中：a、b分别为地基处理范围长边和短边尺寸，有A=ab；θ为应力扩散角，对于刚性底板下的柔性垫层如砂砾石，当地基土较为软弱时，可取θ=25°^［2］。

考虑桩土变形协调，对于加固区①，柔性桩的变形应该等于桩间土的变形，根据公式（14）～（16），有：

也即：

由公式（21）可以求得n₂₁。

对于加固区①和②，刚性桩的变形应该等于桩间土的变形，根据公式（12）～（13）以及公式（16）～（17），有：

也即：

由公式（23）可以求得n₁₁。

将上述求得的n₁₁和n₂₁代入公式（9）可以求得β₃，将β₃代入公式（5）可以求得β₁，由公式（7）求得n₁₂，由公式（6）求得β₂。至此，上述公式（1）～（23）中的未知量n₁₁、n₂₁、n₁₂以及β₁、β₂、β₃都得到解答。

复合地基加固区沉降为

在上述分析中，根据第二节保证桩土变形协调的2个条件，刚性桩和柔性桩均宜设置为摩擦型桩，其桩顶所受压力全部由桩周土体所提供的侧摩阻力承担，桩端压力为0。这是摩擦型桩的理想化情况，实际工程中桩端或多或少都会存在压力，可以通过桩顶所受压力扣减桩周土体侧摩阻力得到。对于端承摩擦型桩（桩底有压力）的情况，只需要在摩擦型桩的基础上考虑刚性桩、柔性桩在桩端产生向下的刺入量即可，其他分析类似，在此不再赘述。上述推导同样适用于单桩型复合地基加固区的沉降计算。

3 复合地基承载力计算

上述分析推导过程，由于不涉及复合压缩模量的计算问题，避免了采用桩体压缩模量通过面积加权平均来获得复合压缩模量而导致的加固区沉降计算值偏小的缺陷；同时，上述过程求得的刚性桩、柔性桩及桩间土承载力特征值发挥系数β₁、β₂、β₃，可以准确确定复合地基承载力：

该式可以较好地解决复合地基承载力发挥系数取值的不确定性问题。

4 工程算例

4.1 算例1

广东省芦苞大型水闸采用CFG桩复合地基进行处理^［15］。根据文献［15］中图5（地质剖面图）和表1，CFG桩均长22.0 m，共布置451根，桩直径为500 mm，桩体压缩模量取1 500 MPa。闸室底板尺寸为92.0 m×22.0 m×2.0 m（长×宽×厚），CFG桩面积置换率为0.043 7。根据CFG桩桩身范围内不同土层的厚度和变形模量，将成层地基转换为均质地基，得到地基平均变形模量约88.3 MPa。根据天然地基的p-s曲线可以得到天然地基承载力特征值约135 kPa，桩端下为卵石粗砂层。桩顶与基础之间铺设300 mm粗砂垫层，垫层变形模量为80 MPa，泊松比为0.3。设计要求复合地基承载力特征值为300.0 kPa。

将上述参数代入，根据公式（18），求得应力扩散系数为0.423；根据公式（21），求得桩土应力比为15；根据公式（8），求得桩间土承载力特征值发挥系数β₃为1.378；根据公式（16），求得CFG桩加固区变形为33.0 mm。

为了说明桩体压缩模量的敏感性问题，同时根据上述步骤对桩体压缩模量分别为1 000 MPa和2 000 MPa的情况进行了计算，得到加固区变形值分别为30.7 mm和36.5 mm。

文献［15］实测资料表明，复合地基沉降为24～35 mm。根据该文献的观点，由于桩底以下为卵石粗砂层，其沉降可以忽略不计，即不考虑非加固区沉降。当桩体压缩模量分别为1 000，1 500，2 000 MPa时，利用本文计算方法得到的加固区沉降依次为30.7，33.0，36.5 mm，如果和文献［15］一样忽略非加固区沉降，则本文方法计算值与实测值具有较好的吻合性。

当桩体压缩模量分别为1 000，1 500，2 000 MPa时，由于桩土应力比介于11.5～17.8之间，桩间土承载力得到了较好的发挥，β₃介于1.281～1.523之间，与可挤密地基中挤土桩施工后桩间土地基实际承载力比天然地基承载力有较大幅度提高的认识一致。

4.2 算例2

杭州市某塔形商住楼^［16］采用长-短桩复合地基进行处理，场地处理范围为30.84 m×14.70 m（长×宽）。钢筋混凝土长桩共44根，直径500 mm，桩长37 m，桩身压缩模量30 000 MPa。水泥搅拌桩共60根，直径600 mm，桩长9 m，桩身压缩模量360 MPa。碎石垫层厚0.15 m，压缩模量105 MPa，泊松比为0.35。长桩桩端处土层为中风化岩层，外部荷载为74 168 kN，天然地基承载力取70 kPa。

根据文献［16］中表2，可以得知短桩范围内土体加权平均压缩模量为8.4 MPa，短桩桩端至长桩桩端范围内加权平均压缩模量为13.69 MPa。根据长-短桩平面布置，可知长桩和短桩面积置换率分别为 0.019 和0.037。

将上述参数代入，根据公式（18）和公式（19），求得短桩和长桩处应力扩散系数分别为0.50和0.141；根据公式（21）和公式（23），求得短桩和长桩各自的桩土应力比为5.44和371；根据公式（8），求得桩间土承载力特征值发挥系数β₃为0.284；根据公式（16）和公式（17），求得加固区变形为s_s1+s_s2=28.8 mm。当与文献［16］一样不考虑长桩桩端下卧层（非加固区）压缩量时，则按照本文方法计算得到的地基沉降量为28.8 mm。

根据公式（12），长桩向上刺入碎石垫层深度为24.2 mm，该数值明显大于文献［16］中的实测地基平均沉降量（8.8 mm）。由于文献［16］未对是否考虑长桩刺入碎石垫层的刺入量做出说明，因此如果考虑，则文献［16］地基平均沉降量应该为实测地基平均沉降量加上长桩向上刺入碎石垫层的刺入量，即8.8+24.2=33.0 mm，与本文计算值（28.8 mm）较为接近。

4.3 算例3

南京浦镇车辆厂生活区由十多栋多层住宅楼组成^［6］。场地土体自上而下分别为：粉质黏土，地基承载力标准值为90 kPa，压缩模量为4.46 MPa，厚约1.0 m；淤泥质粉质黏土，地基承载力标准值为60 kPa，压缩模量为2.82 MPa，层厚13～18 m；粉土，地基承载力标准值为105 kPa，压缩模量为6.16 MPa。

设计要求地基承载力特征值达到160 kPa。采用桩径为500 mm，桩长为15.5 m的CFG桩复合地基进行处理，桩体压缩模量取1 500 MPa。CFG桩总根数为63根，处理面积约a×b=12 m×6.3 m=75.6 m²。桩顶与基础之间铺设300 mm粗砂垫层，垫层模量为50 MPa，泊松比为0.3。

将上述参数代入，根据公式（18），求得应力扩散系数为0.138；根据公式（21），求得桩土应力比为245；根据公式（8），求得桩间土承载力特征值发挥系数β₃为0.043；由公式（16），求得加固区变形为11.65 mm。

根据文献［6］中表2，桩端下卧层沉降量为37.64 mm，则根据本文方法计算得到的地基总沉降量为49.29 mm，与实测地基沉降量46 mm（280 d）较为接近。

4.4 讨 论

分析上述3个算例，发现算例1桩间土承载力特征值发挥系数较大，超过1.0；而算例2和算例3桩间土承载力特征值发挥系数较小，特别是算例3，桩间土实际承担的承载力仅为3.87 kPa，远小于其承载力标准值（90 kPa）。在对某水闸工程刚性管桩复合地基的研究中^［17］，也发现桩间土实际承担的承载力为2.5 kPa，承载力发挥系数仅为0.071。根据规范^［1-2］，桩间土承载力特征值发挥系数β₃可取0.5～0.9。上述算例表明，规范建议的β₃值在某些工程中有可能被高估，造成复合地基承载力计算值偏高，工程偏于不安全；而在某些工程中有可能被低估，工程偏于保守。

在复合地基设计时，上部荷载可以由桩来承担，也可以由桩间土来承担，例如刚性桩复合地基，由于刚性桩强度较大，原则上可以由刚性桩多承担荷载，以减小桩间土承担的荷载，但使刚性桩多承担荷载是有条件的，即桩要能够产生与其承担的荷载相应的变形。因此，就复合地基设计来说，桩及桩间土的承载力发挥系数并非独立取值，而是密切关联的，否则即使按照复合地基承载力计算公式得到的承载力能够满足安全要求，甚至安全裕度还很大，也有可能造成实际工程中复合地基发生破坏的情况。

根据上述分析，用事先假定桩及桩间土承载力特征值发挥系数来确定复合地基承载力及沉降的做法值得商榷，一旦桩间土承载力被过高设计，而实际桩间土承载力并没有按设计发挥作用，这样设计的复合地基往往偏于不安全。

5 结 论

本文以刚-柔性桩复合地基为代表，分析得到了一种复合地基设计方法。

（1） 复合地基的形成条件是桩及桩间土必须共同直接承担上部荷载，因此桩及桩间土必须保证变形协调。保证桩土变形协调的前提条件是：① 刚性桩刺入垫层的深度不能超过垫层厚度；② 刚性桩和柔性桩均宜设置为摩擦桩，这也是复合地基垫层厚度设计的基本原理。对于只有一种竖向增强体的复合地基，如水泥土搅拌桩复合地基，其垫层厚度设计原理与此相同。

（2） 基于静力平衡和桩土变形协调，从理论上得到了复合地基的桩土应力比和各自的承载力特征值发挥系数，进而可以较为准确地得到复合地基加固区沉降，解决了目前采用复合压缩模量方法低估加固区沉降的缺陷。

（3） 根据计算得到的承载力发挥系数，可以准确确定复合地基承载力，解决了目前复合地基承载力确定中由于主观性较强而导致的计算结果偏大问题。

（4） 工程算例表明，事先假定桩及桩间土承载力特征值发挥系数来确定复合地基承载力及沉降的做法值得商榷，从保证复合地基的有效设计和工程安全的角度出发，相关复合地基规范应该根据桩土变形协调来进行复合地基设计。

值得指出的是，由于岩土工程中影响计算准确性的因素较多，因此本文提出的复合地基设计方法也是一种半理论半经验方法，尚需进一步在实践中进行完善。

参考文献：

［1］中华人民共和国住房和城乡建设部.刚-柔性桩复合地基技术规程：JGJ/T 210-2010［S］.北京：中国建筑工业出版社，2010.

［2］中华人民共和国住房和城乡建设部.复合地基技术规范：GB/T 50783-2012［S］.北京：中国计划出版社，2012.

［3］中华人民共和国住房和城乡建设部.建筑地基处理技术规范：JGJ 79-2012［S］.北京：中国建筑工业出版社，2012.

［4］中华人民共和国住房和城乡建设部.建筑地基基础设计规范：GB 50007-2011［S］.北京：中国建筑工业出版社，2011.

［5］闫明礼，曲秀莉，刘伟，等．复合地基的复合模量分析［J］.建筑科学，2004（4）：27-32.

［6］杨光华，徐传堡，李志云，等.软土地基刚性桩复合地基变形计算的简化方法［J］.岩土工程学报，2017，39（增2）：21-24.

［7］刘吉福，郑刚，龚晓南.附加应力法计算刚性桩复合地基路基沉降［J］.岩土工程学报，2018，40（11）：1995-2002.

［8］刘彬.长短桩布桩方式对复合地基沉降变形影响研究［J］.人民长江，2019，50（7）：144-149.

［9］李强，赵海丰，刘国栋，等.减沉桩与加筋土褥垫层联合作用减沉机理研究［J］.人民长江，2015（14）：58-60，79.

［10］彭良泉.刍议多桩型复合地基的设计方法［J］.土工基础，2023，37（5）：802-806.

［11］周同和，王非，赵宏，等.多桩型刚性承台下刚性长短桩复合地基载荷试验分析［J］.岩土工程学报，2015（1）：105-111.

［12］王明山，王广驰，闫雪峰，等.多桩型复合地基承载性状研究［J］.岩土工程学报，2005，27（10）：1142-1146.

［13］龚晓南.广义复合地基理论及工程应用［J］.岩土工程学报，2007，29（1）：1-13.

［14］沈珠江.理论土力学［M］.北京：中国水利水电出版社，2000.

［15］杨光华，苏卜坤，乔有梁.刚性桩复合地基沉降计算方法［J］.岩石力学与工程学报，2009，28（11）：2193-2200.

［16］葛忻声，龚晓南，张先明.长短桩复合地基有限元分析及设计计算方法探讨［J］.建筑结构学报，2003（4）：91-96.

［17］刘鹏，杨光华.考虑桩土变形协调的软土刚性桩复合地基设计计算［J］.岩石力学与工程学报，2011，30（增2）：4039-4046.

（编辑：胡旭东）

Design method of composite foundation considering pile-soil deformation coordination

PENG Liangquan^1，2

（1.Changjiang Survey，Planning，Design and Research Co.，Ltd.，Wuhan 430010，China；2.National Dam Safety Engineering Technology Research Center，Wuhan 430010，China）

Abstract：The composite compression modulus obtained by using the compression modulus of pile body is usually larger，which leads to the underestimate of the settlement of composite foundation reinforcement area.In addition，the selection of bearing capacity coefficient between piles and soil is subjective，resulting in a larger calculation result of the composite foundation bearing capacity.In view of the above two problems，starting from the formation mechanism of composite foundation，we point out that the pile-soil deformation must be coordinated when the pile and the soil bear capacity together.The conditions for the coordination of pile-soil deformation are as follows：①the depth of pile penetration into the cushion cannot exceed the thickness of the cushion；② piles should be set as friction pile.Under this premise，the settlements of piles and soil between piles were calculated respectively.The theoretical values of pile-soil stress ratio and bearing capacity coefficient were obtained by using pile-soil deformation coordination method.Further the settlement calculation method of reinforcement area was given.The engineering example shows that the design of composite foundation should be carried out according to the deformation coordination of pile-soil from the perspective of ensuring the effective design and engineering safety of composite foundation.

Key words：composite foundation；pile-soil deformation coordination；bearing capacity coefficient；pile-soil stress ratio；settlement