基于改进AHP及云模型的水轮机调节系统状态评价

张彬桥 杨洋 刘雷 马昭

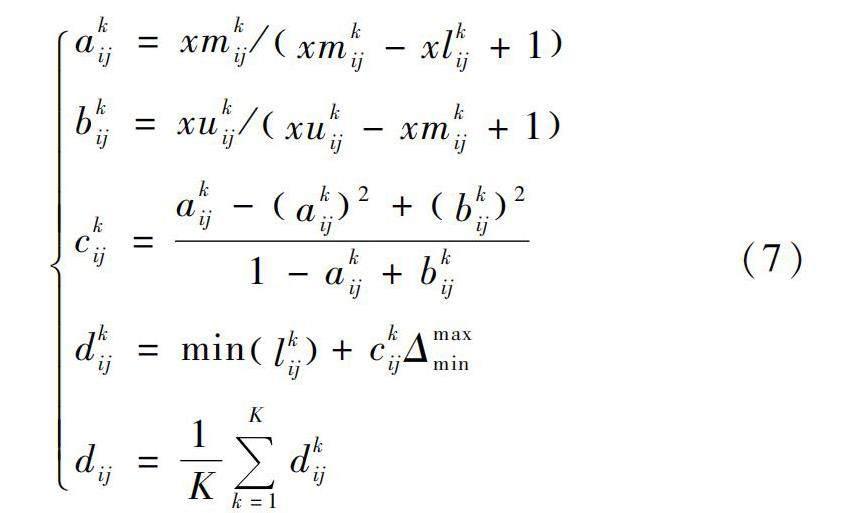
摘要：针对水轮机调节系统综合评价不够全面，无法综合反映系统多指标、多层次的复杂性问题，提出了基于模糊层次分析法（AHP）-决策与实验室评估法（DEMATEL）-云模型的水轮机调节系统综合评价模型。首先建立基于主要设备和相关工况的多层次指标体系，采用模糊AHP计算评价指标的初始权重；通过DEMATEL法计算评价指标的相互影响与参照关系，绘制出指标因果关系图，并结合初始权重计算评价指标的综合权重；引入云模型得到评价指标各等级的隶属度矩阵。最后将权重结果与隶属度结合，得到系统综合评价等级。算例分析表明，该方法可高效快捷地对水轮机调节系统运行状态进行客观评价，为状态检修提供参考依据。

关 键 词：水轮机调节系统；综合评价；三角模糊理论；云模型；DEMATEL

中图法分类号：TV74；TM62

文献标志码：A

DOI：10.16232/j.cnki.1001-4179.2024.05.029

0 引 言

水轮机调节系统在水力发电过程中处于重要地位，对发电质量和系统安全性、经济性有重要影响，水轮机调节系统状态分析评价是水电站运维检修的重要内容。当前大多数水电站采用的仍是“预防性维护检修”，往往会出现维修不足与维修过剩的情况^［1］，影响电站的经济效益和正常运转。

目前针对水轮机^［2］、风电机组^［3］等设备开展的状态评估相关研究中，常见评估方法有信号时域分析法^［4］、神经网络^［5］、专家系统^［6］等。模糊综合评价方法以模糊数学为理论依据，因其不过多依赖先验数据，具有较好的普适性，在工程领域受到广泛研究和关注。石宜金等^［7］引入皮尔逊相关系数，建立了变压器模糊综合评价模型；王玉梅等^［8］在断路器评估中采用灰色变权模糊综合评判，综合了评估模糊性和灰色性。

针对水轮机调节系统的状态评估研究，熊涛等^［9］引入层次分析法（AHP），初步实现对调节系统的模糊综合评估。谢加荣等^［10］采用sigmoid形隶属度函数对三角形隶属度函数进行优化，得到系统综合状态。上述方法均采用传统AHP计算指标权重，未考虑同层指标的相互影响，权重确定缺乏客观性、全面性，影响评估结果准确性。但有学者认为，可通过引入决策与实验室评估法（DEMATEL）^［11］修正AHP缺陷，得到更加科学、准确的权重指数。同时，水轮机调节系统运行环境及工况复杂，在综合评价体系的构建中存在模糊性、不确定性，与模糊评价法使用的定性隶属度函数难以适配，而云模型方法^［12］较好地考虑了数据随机性，可通过模糊化实现定性评估到定量评估的转换。

针对现有水轮机调节系统状态评估方法的不足，本文提出了融合模糊AHP、DEMATEL和云模型的水轮机调节系统综合评价方法，并引入评价指标劣化度算子，避免水轮机调节系统状态评价中专家评分的主观性和繁琐性，有效增强评价参数赋值的可信度。

1 调节系统综合评价指标体系和流程

根据调节系统结构特征以及运行原理^［13］，建立符合实际应用的水轮机调节系统状态运行3层指标体系——A目标层、B准则层、C指标层。本文选取漏油量、油泵泵油时间、油泵启动间隔等22个评价指标，如图1所示。

本文引入模糊AHP、DEMATEL和云模型方法对水轮机调节系统的运行状态进行综合评价，基本思路是采用模糊AHP和DEMATEL方法计算指标的综合权重，然后运用劣化度算子和云模型建立评价指标各等级隶属度矩阵，最后结合综合权重，根据最大隶属度原则确定水轮机调节系统的状态等级，流程见图2。

2 基于模糊AHP-DEMATEL-云模型的综合评价方法

2.1 模糊AHP计算初始权重

传统的层次分析法广泛应用于赋权问题，具备简单实用的优点，但是考虑专家主观意识和模糊环境下的不确定性，难以得到科学合理的判断矩阵。引入三角模糊数可解决传统AHP主观性较高且误差大的问题。根据表1收集专家评价，假设共有T个专家对n个指标进行两两比较，利用三角模糊数对其不确定性进行定量分析。

（1）获取第t个专家的判断结果a^t_ij：

计算全部专家判断结果的均值，得到三角模糊矩阵A

式中：m表示专家判断的理想值，l为模糊下限，u为模糊上限，l与m差距越大判断越模糊，反之判断越精确。

（2）通过矩阵A构建模糊判别因子矩阵E。

式中：e_ij=（u_ij-l_ij）/2m_ij，记为标准离差率，此数值越大说明模糊程度越大，但可信度越小；反之模糊程度越小，可信度越大。

（3）构建调整判断矩阵Q。

（4）依据线性代数列变化，将矩阵Q转换成对角线均为1的判别矩阵H，并分别求判别矩阵H每行元素f_ij乘积的n次方根，将其归一化，得到初始权重向量w′_i。

2.2 模糊DEMATEL确定指标影响关系

决策实验室分析法即DEMATEL法，运用图论和矩阵对系统内部要素的不确定关系进行分析。通过计算指标因素的中心度，确定指标相互影响关系和影响程度。引入表2的三角模糊数建立专家术语与模糊数之间的映射关系，弥补专家判断的主观性和差异性。

1. 根据专家意见建立初始直接影响矩阵，设专家k给出的评定结果为s^k_ij=（l^k_ij，m^k_ij，u^k_ij），利用CFCS方法^［14］去模糊化，计算标准化的三角模糊数。

式中：Δ^max_min为初始三角模糊数最右侧值与最左侧值之差。

（2）依次计算左右标准值a^k_ij、b^k_ij，标准化总值c^k_ij，精确值d^k_ij以及K位专家评论的精确值均值d_ij。

1. 直接关系矩阵D等价标准化，计算综合影响矩阵T。

式中：I为单位矩阵。

（4）计算指标因素的影响度e，被影响度f，中心度m，原因度h。

2.3 模糊AHP-DEMATEL计算综合权重

对指标各中心度归一化得到修正权重，然后结合初始权重计算综合权重。

式中：w″_i为修正权重值；w′_i是初始权重；W_i为最终的综合权重。

2.4 基于云模型计算综合评价等级

云模型最早由李德毅院士提出，以3个数字特征期望E_x（表示定量描述的值）、熵E_n（表示影响因素的取值范围）、超熵H_e（表示影响因素的离散程度）描述。通过Matlab生成正态隶属云图实现模糊、随机环境下定量值对定性概念的数字化展现。

（1）鉴于评级指标因素量纲和数量级的不同，本文以相对劣化度进行标准化处理。

对正向指标即越大越优型进行标准化：

式中：C_max、C_min表示正向指标的理想值和极限值；C_i表示实测值。

对负向指标即越小越优型进行标准化：

式中：C′_min、C′_max表示负向指标的理想值和极限值。

（2）将调节系统综合评价划分为5种状态等级，基于指标劣化度及黄金分割确定标准云的评价范围以及数字特征如表3所列，超熵由经验取值0.05^［15］。

根据云数字特征，在Matlab中生成状态评价等级指标标准云图如图3所示。

（3）计算评价指标隶属度矩阵。根据指标的劣化度值x计算与正态云模型之间的各等级云隶属度μ向量，考虑隶属度的随机性，通过1 000次计算求均值。

式中：E′_n=normrnd（E_n，H_e），是以熵为均值、超熵为标准差的正态随机数。

对于n个评价指标分别运用云模型计算各等级隶属度，形成隶属度矩阵U。

式中：μ_ij表示指标i归属于综合评价等级j的隶属度值。

（4）计算综合评价结果向量。根据综合权重W和隶属度矩阵U，由式（13）确定调节系统A的综合评价结果向量。

U_A=W×U=（U¹_A，U²_A，U³_A，U⁴_A，U⁵_A）（14）

式中：Uⁱ_A（i=1，2，3，4，5）表示调节系统A对应于5种评价等级的隶属度。

3 算例分析

根据式（11）～（12）对某水电站调节系统某时刻运行数据进行初始化处理，结果如表4所列。

3.1 综合权重确定

3.1.1 模糊AHP计算初始权重

采用式（1）～（2）将专家意见转为定量的三角模糊矩阵。根据式（3）～（5）自上而下递归计算，以此量化底层指标对于评价顶层主体的重要程度，结果如表5所列。

3.1.2 模糊DEMATEL确定指标影响关系

基于DEMATEL方法，根据式（6）～（9），计算评价指标的影响度、被影响度、原因度、中心度，具体数据如表6所列。

根据数据建立中心度与原因度的因果关系，如图4所示。原因度为正值的指标表明这些指标在系统中容易对其他指标造成影响，称其为原因指标；原因度为负值的指标则表示它们在系统中容易被其他指标影响，称其为结果指标。

3.1.3 模糊AHP-DEMATEL计算综合权重

根据式（10）对评价指标的初始权重以及中心度下的修正权重进行综合，得到综合权重为W=（0.025 9，0.037 6，0.053 4，0.028 7，0.048 2，0.027 6，0.044 1，0.056 6，0.051 2，0.015 5，0.062 8，0.074 0，0.049 8，0.089 0，0.073 9，0.051 2，0.081 1，0.044 0，0.030 8，0.037 6，0.011 1，0.006 1），各权重分布如图5所示。

3.2 评价指标隶属度矩阵

将表6中各指标的相对劣化度代入云模型，根据式（13）计算取均值，得到水轮机调节系统各指标的隶属度矩阵如表7所列。

3.3 水轮机调节系统综合评价结果

根据上述所求综合权重W与隶属度矩阵U，由式（13）确定调节系统状态评估结果为

U_A=W×U

=［0.01820.27070.51950.10530.004］

矩阵U_A表示本实例中的水轮机调节系统综合评价结果，如表8所列。

根据隶属度最大原则该水轮机调节系统整体处于“中等”状态，由于“良好”状态的隶属度（0.2707）大于“注意”状态（0.1053），因此系统整体处于中等偏上水平。同理可得，调节系统的子系统辅助油系统为“良好”状态；开机工况为“良好”状态；停机工况为“中等”状态；带负荷工况为“中等”状态；甩负荷工况为“中等”状态；水力系统为“中等”状态；运行可靠性为“良好”状态。

4 结 论

（1）将三角模糊数引入AHP解决了语义模糊、主观性强、过度依赖专家经验等问题。采用DEMATEL对AHP法进行修正，考虑了指标间的影响关系，得到的综合权重更具可信度，提高了评估的准确性。

（2）建立了符合实际的水轮机调节系统状态评估的多层次模型，并将模糊综合评价与云模型结合建立了模糊综合评价模型，考虑了不确定性的映射关系，最终实现了调节系统整体及其子系统的运行状态综合评价。该结果可为工作人员确定水轮机运行状态和趋势提供准确有效的意见，为水轮机调节系统综合评价提供了新方法。

参考文献：

［1］钟旭，张宝源，孟威，等.基于VMD-TCN的水电机组健康状态监测系统设计［J］.水利水电快报，2024，45（2）：44-47.

［2］宋科，杨邦成，段维华.偏流条件下潮流能水轮机的熵产特性评估［J］.水力发电学报，2022，41（8）：12-19.

［3］李进友，李媛，冯冰，等.基于随机组合赋权模糊评价的风电机组健康状态评估［J］.太阳能学报，2022，43（8）：340-351.

［4］黎梓昕，林海军，徐雄，等.基于KPCA-PSO-SVM的水轮机组故障检测方法［J］.排灌机械工程学报，2023，41（5）：467-474.

［5］王力，刘子奇.WPA-IGA-BP神经网络的模拟电路故障诊断［J］.系统工程与电子技术，2021，43（4）：1133-1143.

［6］邓军，陈东，秦立斌，等.多层面、多维度输电线路运维辅助决策专家系统［J］.信息与控制，2015，44（5）：612-621

［7］石宜金，谭贵生，赵波，等.基于模糊综合评估模型与信息融合的电力变压器状态评估方法［J］.电力系统保护与控制，2022，50（21）：167-176.

［8］王玉梅，张胤.基于云模型与变权灰色模糊综合评判的真空断路器状态评估［J］.制造业自动化，2020，42（2）：94-98.

［9］熊涛，周建中，付文龙，等.基于模糊层次分析法的抽水蓄能机组调节系统状态综合评估［J］.水电能源科学，2016，34（9）：170-172.

［10］谢加荣，蔡卫江，邢红超，等.抽水蓄能机组调速系统健康状态评估［J］.水电能源科学，2020，38（4）：134-137，196.

［11］CHENG L H，CAO D Q，GUO H M.Analysis of coal mine occupational disease hazard evaluation index based on AHP-DEMATEL［J］.Archives of Environmental & Occupational Health，2021，76（7）：372-384.

［12］田林钢，高佳东，巴超，等.强降雨条件下土石坝安全评价［J］.人民长江，2021，52（6）：195-200.

［13］蔡燕生，龙建明，李爱民.水轮机调节［M］.郑州：黄河水利出版社，2009.

［14］薛松，张珍珍.基于Fuzzy-DEMATEL的PPP项目协同监管影响因素识别与分析［J］.软科学，2021，35（7）：104-109，115.

［15］崔玉海，吴泽宁，吴丽.基于云模型的安阳市洪水灾害风险评价［J］.人民长江，2020，51（7）：7-12.

（编辑：郭甜甜）

Operation status evaluation of hydraulic turbine regulation system based on

improved AHP and cloud model

ZHANG Binqiao^1，2，YANG Yang^1，2，LIU Lei^1，2，MA Zhao³

（1.Hubei Provincial Key Laboratory for Operation and Control of Cascaded Hydropower Station，China Three Gorges University，Yichang 443002，China；2.College of Electrical Engineering & New Energy，China Three Gorges University，Yichang 443002，China；3.Datang Yunnan Power Generation Co.，Ltd.，Kunming 650000，China）

Abstract：Comprehensive evaluation of hydraulic turbine regulation system is not comprehensive enough and cannot comprehensively reflect the complexity of the multiple indicators and levels of the system，so a comprehensive evaluation on hydraulic turbine regulation systems based on the fuzzy analytic hierarchy process （AHP）-decision and laboratory evaluation method（DEMATEL）-cloud model was proposed.Firstly，a multi-level index system based on major equipment and relevant working conditions was established，and the initial weight of evaluation indexes was calculated by fuzzy AHP；the mutual influence and reference relationship of evaluation index was calculated by DEMATEL method，and the index causal relationship diagram was drawn，and the comprehensive weight of evaluation indexes was calculated in combination the initial weight；the membership degree matrix of each level of evaluation index was obtained by introducing cloud model.Finally，the weight results were combined with the membership degree to obtain the comprehensive evaluation grade of the system.The case analysis showed that this method can make an objective evaluation on the operation status of hydraulic turbine regulation system efficiently and quickly，providing a reference basis for state maintenance.

Key words：hydraulic turbine regulation system；comprehensive evaluation；triangular fuzzy theory；cloud model；DEMATEL