对一道椭圆题的研究

朱云燕

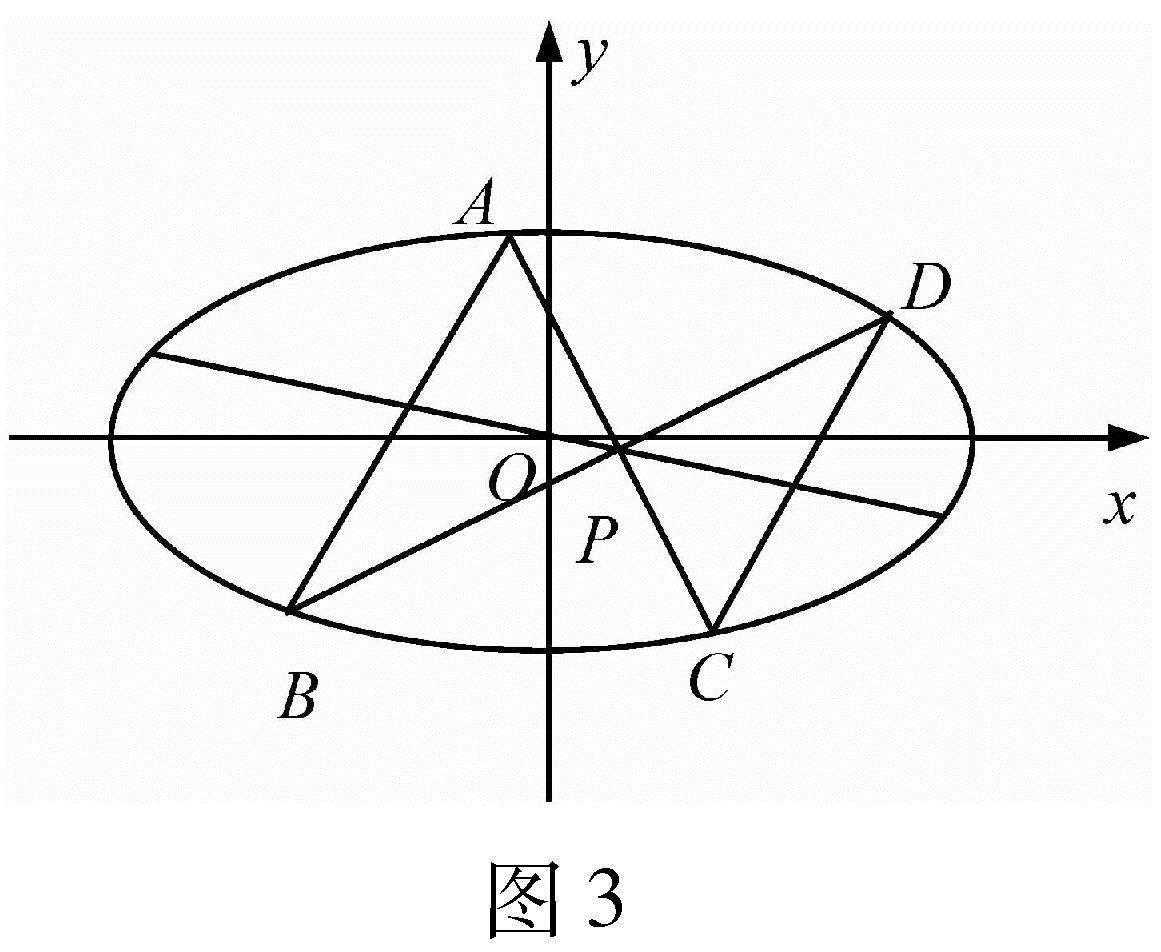
在教学中，笔者最近讲了下面的一道椭圆题：

（1）求椭圆的方程；

（2）求证：直线CD的斜率为定值．

第（2）问求得直线CD的斜率为定值kCD=2，发现AB//CD．

作为教师，我们不能仅仅停留在思考如何解决这个问题的层次，还要继续前进，研究问题是如何提出来的，学会命题．研究问题的背景、本质，研究问题的一般情形，达到更高境界．为启发学生、帮助学生，做好充分的准备工作．

1．题1的背景探究

对于此题，通过逐步提问的方式，探索问题的背景、弄清问题的由来、揭示问题的本质．

为叙述方便，引入几个定义．

定义1 连接椭圆上任意两点的线段叫做弦．

定義2 经过椭圆中心的弦叫做椭圆的直径．

定义3 平行于椭圆一条直径的弦的中点的轨迹和该直径叫做椭圆的一对共轭直径．

至此，我们明白了点P落在椭圆直径AB的共轭直径EF上．

2．第（2）问的一般情形

将题1的第（2）问进行一般化得到：

P是线段EF上异于E，F的一点，直线AP，BP与椭圆的另一交点分别为C，D．则AB//CD．

再一般化推广，于是便得到椭圆内接四边形对边平行的一个充要条件．

3．椭圆内接四边形对边平行的一个充要条件

由于一般是对特殊的概括，特殊是一般的具体表现，一般深刻，特殊鲜活、生动．从一般的命题2可以演绎出大量的特殊、生动的问题．

4．命题2的特殊情形

以上证明直线平行，并没有证明直线的斜率相等，而是设出线段的比值，利用线段成比例证明平行．

除了运用命题2的结论来命制题目外，我们还可以用解决命题2的方法命制题目．

5．用解决命题2的方法来命制题目

以上先把一道具体的题目推广到一般情形，从特殊到一般，揭示问题的本质．再利用一般结论，从一般到特殊，命制新的题目．最后再利用解决问题的方法命制新题，不但重视结论的应用，而且重视解决问题方法的应用．数学学习不但要重视结果的学习，还要重视过程的学习，要全面掌握解决问题的方法，形成解决问题的结构性、系统性方法，更全面地分析问题解决问题．例如，刻画点共线，不但可用斜率、直线方程，也可以用向量共线等，证明直线平行，不但可以证明直线的斜率相等，也可以用线段成比例来证明，简洁解决问题．解析几何中的大多题目都有着一般背景，我们要深入研究这些背景，把题目系列化、系统化，切实减轻学生的作业，实现提质增效．深入研究圆锥曲线的性质，充分揭示题目的背景，得出简洁、和谐、深刻的结论，发现它们之间奇妙的关联，给我们以美的享受，让我们更爱数学，更爱数学教育．