整体建构多向关联 核心问题分层进阶

【摘   要】问题序列能有效链接知识概念，引发学生的认知冲突，并为探究路径奠定基础，从而促进学生对相关知识概念的深度理解和知识结构的建立。以“圆的再认识”的教学为例，通过“单元整体解读，聚焦本质关联；把握学情特征，明确目标定位；提炼核心问题，思维分项进阶”的问题链驱动式教学策略，能引领学生的学习不断走向深处，进而发展学生的高阶思维。

【关键词】问题链；多向关联；分层进阶

在实际教学中，不少教师在课堂上提出的问题或多或少都存在琐碎、随意、封闭等问题，导致数学本质指向模糊以及知识链接断裂，进而使学生的思维空间受限。为解决这些问题，笔者所在团队积极探索构建问题链的有效方式，以促进学生的深度学习并构建结构化认知。

问题链是教师根据教学内容和教学目标，精心提炼出核心问题及其驱动性子问题，从而形成的具有逻辑关联的问题序列。这样的问题序列能有效链接知识概念，引发学生的认知冲突，并为探究路径奠定基础，从而促进学生对相关知识概念的深度理解和知识结构的建立。下面以“圆的再认识”的教学为例，具体阐述问题链的生成、架构以及在教学中的应用。

一、單元整体解读，聚焦本质关联

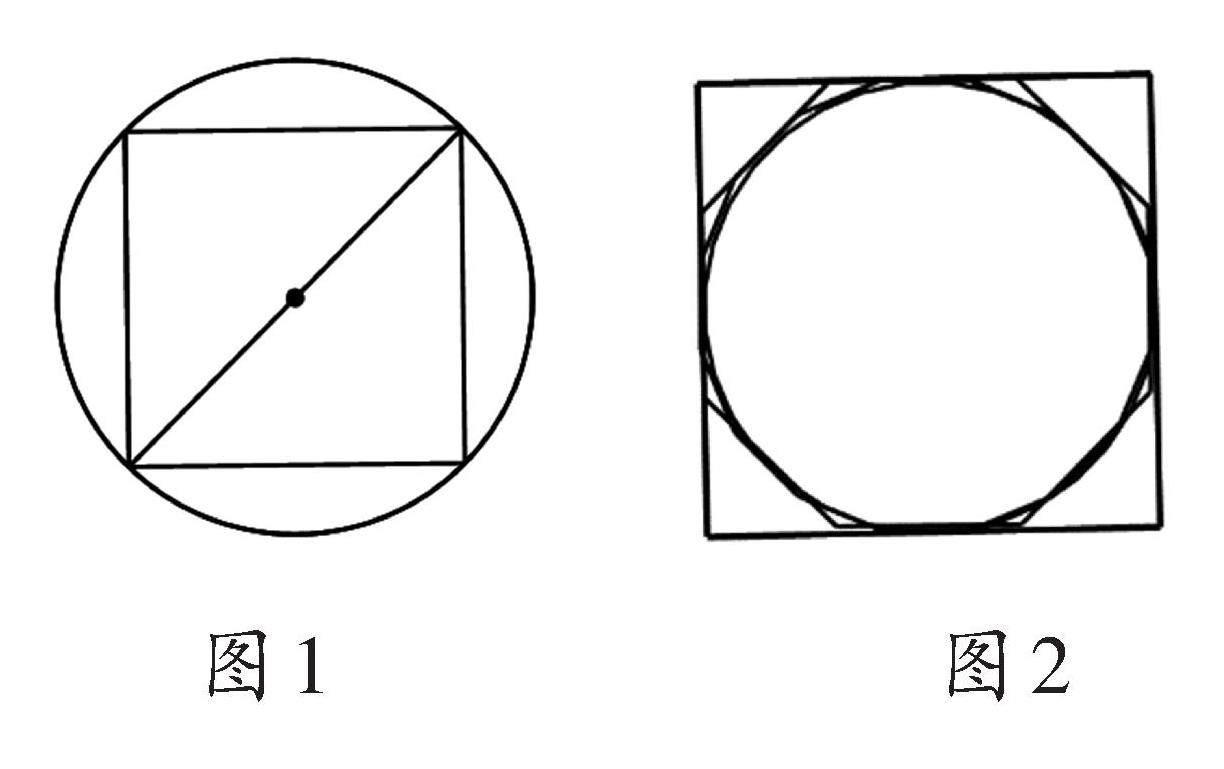
中国古代数学著作《周髀算经》中说：“圆出于方。”这揭示了圆与方之间的内在关系。这里的“方”指正方形，有两种解释：一是以正方形对角线的中点为圆心旋转对角线，即可得到圆（如图1）。二是通过不断切去正方形的角，将其逐渐转化为边数更多的正多边形。随着边数的增加，其形状逐渐逼近圆（如图2）。这两种解释都揭示了正多边形与圆之间的关联，也为认识圆提供了教学思路。

目前多个版本的教材都对正多边形与圆的关系进行了深入探讨。其中，人教版教材和苏教版教材都提及了刘徽的割圆术：“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣。”意思是不断增加正多边形的边数，使其从正六边形逐渐变化为正十二边形、正二十四边形等。当边数趋于无穷时，正多边形的形状将无限接近圆（如图3），从而求得圆周率的近似值是3.14。而北师大版教材则引用了阿基米德的研究，通过对比圆的外切正多边形和内接正多边形，进一步验证了“圆内接正多边形边数增加时，其面积逐渐逼近圆的面积”（如图4）。

在教学中，教师可以引导学生沿着古人的研究路径，自主发现正多边形与圆之间的这种紧密联系。同时，鼓励学生深入探究正多边形变化过程中周长和面积的变化规律。在后续的教学中，教师还可以引导学生利用刘徽的割圆术来探究圆周率，进而计算圆的周长。利用阿基米德的研究，进一步说明“圆内接和外切正多边形的边数越多，其面积越大，而圆的面积则是最大的”。

二、把握学情特征，明确目标定位

问题的来源不应仅限于教材，还应紧密关联学生的学习基础和经验。教师需要根据学生的认知特点，明确教学目标，提炼核心问题。为此，笔者设计了相关的前测题，用以检测学生的认知起点。

（一）对正多边形的认知

【前测题1】下列哪些图形是正多边形？你认为怎样的图形是正多边形？

从测试结果来看，大部分学生能够准确识别正多边形，部分学生还从边的长度和角的角度对正多边形进行了思考。尽管他们尚不能准确描述正多边形的定义，但已对正多边形有了初步的认识。

（二）对圆的数学史的了解

【前测题2】你知道有哪些数学家研究过与圆相关的内容吗？他们分别有什么成就？

从测试结果来看，大部分学生仅知道祖冲之（如图5），对其他数学家，如刘徽、阿基米德等，则知之甚少。这表明学生对数学史的了解相对有限，需要教师引导他们接触更多的数学文化。

（三）对正多边形与圆关系的认识

【前测题3】你认为正多边形和圆之间有联系吗？如果有，请简单说一说。

测试结果显示，有12.8%的学生联想到了方中圆（外方内圆）和圆中方（内方外圆）的情况。近三分之一的学生提到了圆与正多边形的某种联系（如图6）。然而，他们主要关注的是两者的外部特征，因此还需要通过活动引导他们关注两者内部的结构关联，深化他们对极限思想的理解。

基于教材研读和学情分析，确立本内容的教学目标如下。

（1）通过比较正多边形与圆，发现它们之间的内在联系，建立平面图形的知识结构，并在图形的演变中感悟极限思想。

（2）在使用直尺画圆、寻找正多边形边的过程中，运用正多边形与圆的关系解决实际问题，想象图形的变化，了解数学在现实生活中的应用，体会数学之美。

（3）了解圆的研究发展历史，感受古人的智慧，感悟数学文化，掌握科学的数学学习方法。

三、提炼核心问题，思维分项进阶

教师通过教材解读和学情分析，明确本内容的研究主题：正多边形与圆有什么联系？进一步提炼出三个核心问题，并将这些核心问题分解为一系列具有驱动性的子问题（如表1），促进学生的思维不断进阶，学习逐步走向深处。

在研究主题下，核心问题呈现出递进式关系，促进学生思维从感知向领悟、内化进阶。而核心问题下的驱动性子问题既呈现递进式关系，又存在并列式关系，共同促进研究主题的落实。

（一）在分析想象中感知正多边形与圆的联系

在探究正多边形与圆之间联系的过程中，教师需要帮助学生在头脑中形成几何图形的表象。只有建立丰富的表象，才能进行几何图形的特征探究。而表象的形成离不开分析与想象。

【核心问题1】正多边形与圆有关联吗？

● 驱动性子问题：将圆周等分，依次用线段连接等分点，会形成什么图形？

教师出示一个圆，引导学生想象：圆上有3个点，将圆周等分成了3份。依次连接这3个点，会得到什么图形？学生反馈是正三角形。教师顺势引导学生利用正三角形寻找圆的圆心与半径，接着继续提问：“若将圆四等分、五等分、六等分呢？”

● 驱动性子问题：能求出圆内接正多边形的周长与面积吗？

教师出示两个问题：①如果圆的直径是d，正方形的面积是多少？②如果圆的直径是d，正六边形的周长是多少？（两题任选其一）

学生反馈：正方形可以分成2个高是[d2]、底是d的三角形，从而求出它的面积是[d2]×d÷2×2=[d22]（如图7）；正六边形可以分成6个边长为[d2]的正三角形，从而求出它的周长是[d2]×6=3d（如图8）。

在解决问题的过程中，学生发现圆内接正多边形与圆之间确实存在紧密的联系。在此基础上，教师引导学生继续想象：如果将圆周十二等分、二十四等分，依次用线段连接等分点后将会得到什么图形？继续分割下去又会发生什么变化？学生发现：正二十四边形已经很像一个圆。若继续分割，将逐步接近圆形。

通过对圆的不断分割，学生从有限思考拓展到无限想象，从而得到极限思想的渗透与空间观念的培养。而计算圆内接正多边形的周长与面积，进一步展现了正多边形与圆的结构化联系。学生通过充分的想象与计算，初步认识到正多边形与圆的联系。

（二）在关联类比中领悟正多边形与圆的联系

建立丰富的表象是探究几何图形特征的前提。教师要引导学生自主探究正多边形与圆的特征，并关注这些特征在正多边形变化过程中的变动，进一步感悟几何图形之间的联系。

【核心问题2】随着边数的增多，正多边形会发生哪些变化？

在边数逐渐增加的过程中，除形状外，正多边形的面积、周长、对称轴等都会发生相应的变化。教师要引导学生自选其中一个方面进行探究，进一步感受正多边形与圆的联系。

● 驱动性子问题：正多边形的面积有哪些变化？

对比正多边形与外接圆的面积，学生发现：外接圆与正多边形之间空白部分的面积逐渐减小，因而正多边形的面积逐渐增大（如图9）。教师适时提问：“正多边形的面积会无限增大吗？”

● 驱动性子问题：正多边形的周长有哪些变化？

通过图形测量、计算、归纳、概括，学生发现：随着边数的增多，正多边形的周长越来越长，逐步逼近圆的周长（如表2）。

● 驱动性子问题：正多边形的对称轴有哪些变化？

通过画图与想象，学生发现：正多边形有多少条边就有多少条对称轴。随着正多边形边数的增多，其对称轴数量也逐渐增多。而圆有无数条对称轴，且这些对称轴均位于直径所在的直线上（如图10）。

图10

基于此，教师用微视频介绍刘徽的割圆术：刘徽通过极限思想，把圆分割成3072份，最终得到圆周率的近似值3.14，为圆周长和面积的计算作出了巨大贡献。

实际上，正多边形与圆的关联远不止于此，还有从中心点到顶点的距离均相等等。教师可以引导学生通过对对称轴的探究，进一步认识圆的对称性。同时，在周长与面积的变化过程中，再次深入渗透极限思想，为学生后续学习圆周率与圆面积奠定思维基础。

（三）在应用操作中内化正多边形与圆的联系

具身操作是内化知识最好的方式。将正多边形与圆的联系用于解决问题，可以促进学生对知识的正向迁移与内化，使學生的思维水平从结构关联走向抽象扩展。

【核心问题3】如何应用正多边形与圆的关系解决问题？

● 驱动性子问题：你能利用正多边形与圆的关系，只用直尺画圆吗？

教师引导学生思考：怎样只用直尺通过不同的方法画圆。学生反馈：一种方法是根据圆有无数条对称轴画圆；另一种方法是根据“圆出于方”，先画一个正方形，然后不断切割正方形的角，使正多边形的边数越来越多，进而“形成圆”。

无论是哪种方法，都体现了学生对圆更深入的理解和应用。学生在逆向运用圆与正多边形关系的过程中，体会到圆与其他平面图形的联系，并在操作过程中将所学知识付诸实践，从而体会到数学学习的魅力。

● 驱动性子问题：正多边形的顶点两两相连，会变成什么图形？

教师出示相关图形，并引导学生观察想象：如果边数继续增加，图形会发生什么变化？通过动态呈现图形的变化（如图11），验证了正多边形与圆之间的紧密联系。

教师引导学生在解决问题中两次应用正多边形与圆的联系，将它们的关联进行内化，并继续渗透极限思想，引导学生想象，引发学生的认知冲突，让学生将正多边形与圆再次进行关联，从而感悟数学的魅力与美学。

虽然正多边形与圆在本质上是两种截然不同的几何图形——一种是直线图形，另一种是曲线图形，但教师可以从数学史的视角出发，引导学生重走古人的探索之路，将这两种图形进行关联。这不仅能渗透极限思想，提升学生的空间想象力，还有助于促进学生对知识的结构化理解。而这种结构化理解可以为学生后续学习圆周率及圆的面积奠定思维基础。在教学设计上，笔者所在团队则尝试运用问题链驱动的方式，引导学生在学习过程中自主提问、自主探究、自主解决问题，从而形成一种自主学习的范式，以提高学生的学习能力。

参考文献：

［1］邵汉民，陈柏钢.渗透类比与极限   体会联系与区别：基于正多边形的视角进行圆的整体设计的实践研究［J］.小学数学教师，2021（7/8）：97-102.

［2］陈霞.学习材料多向关联   核心任务分层进阶：以人教版教材二年级上册“表内乘法（二）”单元复习为例［J］.教学月刊·小学版（数学），2023（11）：18-22.

［3］鲍善军，朱曙光.“一题一课”的教学价值、设计与策略［J］.教学月刊·小学版（数学），2022（7/8）：12-16.

（浙江省杭州市钱塘区临江新城实验学校）