深度学习的驱动要素

郑金宾 吴婷婷 杜华

【作者简介】郑金宾，正高级教师，天津市第一百中学教科处主任，研究方向为高中数学教学；吴婷婷，二级教师，研究方向为高中数学教学；杜华，高级教师，研究方向为高中数学教学。

【摘 要】本文以“余弦定理”一课的教学为例，针对学生数学学习的现状，对深度学习的驱动要素进行研究，阐明了学科观念、情境、问题、任务、活动、评价等驱动要素的内涵及操作策略，对在课堂上如何驱动学生进行深度学习，促使学习真正发生，发展学生的数学核心素养进行了探索。

【关键词】深度学习；驱动要素；余弦定理

深度学习以学科核心素养为导向［1］，指向学生关键能力、必备品格与正确价值观念的形成，是学生有意义的学习过程。深度学习并不是学生天生就会的，也不是学生能够自发实现的，需要教师充分考虑教情、学情，从教学的诸要素及其结构出发，设计恰当的学习环节驱动学生深度学习的发生。从某种意义上讲，深度学习驱动程度的强弱，决定了深度学习达成效果的好坏。

一、观念驱动

观念是行动的先导。学科观念是学生学习的方向，它对于学生了解问题的背景、缘由、目标导向，明确知识的来龙去脉，学会发现与提出问题，实现进阶式目标具有重要意义，有助于学生掌握知识背后的结构、联系、规律，形成知识与经验的结构化。缺乏学科观念的教学，势必是零散的、碎片化的，容易导致机械解题、盲目刷题的知识本位教学，无法实现知识的应用与根本性迁移，知识能力、道德价值与力量升华也无从谈起。观念驱动功能的發挥取决于学生的数学思维与现实思维切换的程度，对数学学科价值的认同程度等，这关键在于教师学科观念教学的设计与实施水平。深度学习视角下的观念驱动就是要基于学生已有概念系统中的经验和学科知识本质，以数学核心概念为统领，从学科观念出发，给学生强有力的意识引领，对学生进行潜移默化的科学精神、理性思维熏陶，从整体上把握学科知识的内涵，凸显学科知识间的结构、关联和规律，解决好“学什么”“为什么学”“怎么学”“学到什么程度”等问题，实现课程内容的结构化，体现学科育人价值，让深度学习在课堂上真正发生，实现“教是为了不教”的目的。

数学是研究空间形式与数量关系的一门科学［2］。“余弦定理”刻画了任意三角形中的边角关系，是三角函数知识和平面向量知识在三角形中的具体运用，为解三角形提供了基本而重要的工具。为什么要探究一般三角形中的边角关系？如何探究一般三角形中的边角关系？对于多数学生而言，没有形成明确的思想认识、有效的思维方法和一般的学科观念。用学科观念驱动“余弦定理”的深度学习，就要从学习余弦定理涉及的概念、原理、方法、观念出发，触发学生的深度认识。如，数学研究对象既需要定性研究也需要定量研究，那么三角形如何进行定性研究？在定性研究的基础上，又该如何进行定量研究？三角形与哪些数学知识有关联，它们能为三角形问题的解决提供哪些支撑？这些学科观念能够迅速激发学生学习的兴趣，促使学生主动探究、深入思考，提升理性思维。

二、情境驱动

情境是学科观念的载体。好的情境能激发学生的求知欲，诱发学生思考，引发学生自主探究、挑战问题，培养科学精神。好的情境需要真实，脱离了真实性情境的数学学习就会变成“干巴巴”的数学符号的堆砌。浅层学习往往只关注情境本身，而深度学习则关注情境中蕴含的学科本质属性。情境设置的目的不仅仅是去解决情境中的具体问题，更主要的是在问题的解决过程中生发新的数学概念、方法、原理与观念。情境不能是摆设，情境驱动功能的发挥取决于情境能否契合学科观念的培育，契合学科核心概念的形成，契合学科原理的发现，契合学科核心素养的发展。深度学习视角下的情境驱动就是要基于学生学习的现实，从知识内容的逻辑体系出发，真实地再现与学生学习相关的真实世界，指向关键问题，找到数学元素，发现数学主题，提炼数学概念，捕捉数学关系，形成数学结构，欣赏数学美感，彰显数学观念。同时，要关注学生个体行为的即时反应，强调学生个体意识的深度介入，激活学生的知识储备，唤醒学生的活动经验，实现学生知识与经验的相互转化。

三角形源自现实世界，因此“余弦定理”的教学情境必须是真实的。在余弦定理的学习中，多数学生缺乏由定性研究到定量研究的能力。为了强化定量研究的学科观念，可以设置以测量为目标的真实情境：

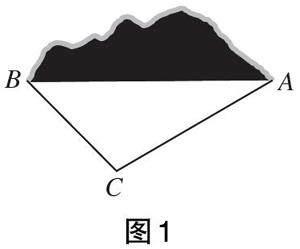
如图1，某隧道施工队为了开凿一条山地隧道，需要测算隧道的长度。工程技术人员先在地面上选一适当的位置C，量出C到山脚A，B的距离，其中CA=3km，CB=1km，再利用经纬仪量出C对山脚AB的张角∠BCA=150°，请回答：隧道AB的长度能否确定？如果能够确定，如何求出其长度？

情境中至少包含以下信息：其一，利用边角边可以判定三角形全等，这个三角形是唯一确定的；其二，三角形的其他元素与给定的元素具有一定的数量关系；其三，研究这种数量关系具有重要的现实意义。这样的情境创设容易激发学生的深度思考，驱动学生深度联系所学知识，那么对三角形边角关系的探究便呼之欲出了。

三、问题驱动

数学是思维的体操，思维需要问题来驱动，问题在情境中产生。通过真实的情境，提出合适的数学问题，促进学生思维的进阶，培养高阶思维，是深度学习的必由之路。在课堂教学中，教师都会提出问题，但为什么有些问题不能驱动学生的深度学习？因为这些问题往往是点状的、孤立的，教师满堂问，学生随意答，问题缺乏挑战性、探究性、启发性，没有将问题的驱动功能发挥出来。问题驱动功能的发挥取决于问题能否有效调动学生进行知识的关联，能否有效启发学生进行知识的多维整合，能否激发学生开展深度的分析、评价、创造等思维活动。深度学习视角下的问题驱动就是要在真实情境中建构数学问题，设计体现主题情境的核心问题，并将其分解为纵横关联的子问题串，建立相应的问题框架，建构明晰完整的以主问题为核心的问题体系。以问题为支架，引导学生积极参与知识“探”的过程，弄清是什么；积极参与知识“究”的过程，弄懂为什么；积极参与知识“用”的过程，学会怎么用；帮助学生“思”有来龙、“想”有去脉、“用”有所属，提升数学思考力和实践力。［3］

“余弦定理”的核心是“在三角形中根据两边及其夹角求出第三条边”，为解决此核心问题，可以将其分解为如下子问题串：

子问题串1 用平面向量方法解决数学和实际问题的“三步曲”是什么？在△ABC中，如何用向量表示问题中涉及的几何元素？这些向量之间有什么内在的联系？

子问题串2 利用“三角形回路”[CB]-[CA]=[AB]，欲求[AB]，应该如何设计运算方案？这种运算与平面向量的什么知识有关？它的运算特点是什么？它的優越性体现在什么地方？运算结果是什么？你还能用其他方法得出余弦定理吗？

子问题串3 你能用恰当的数学语言表示运算结果吗？（如文字语言、图形语言、符号语言等。）余弦定理中的三条边具有什么特性？勾股定理与余弦定理有什么关系？如果已知三角形的三条边，能否确定三个角？

子问题串4 利用余弦定理及其推论可以解决哪几类解三角形的问题？其他类型的解三角形问题能否应用余弦定理及其推论去解决？余弦定理的优势和劣势分别在哪里？

子问题串5 余弦定理与三角形、余弦函数密切相关，你能想到哪些相关性？利用三角函数，你还能把三角形中的哪些定性结论变成可定量计算的数学表达式？依据是什么？

这样，以问题为驱动，通过“情境—问题化”“问题—模型化”的“水平数学化”过程，学生围绕核心问题，在解决循序渐进的子问题串的过程中，实现了知识进阶、思维进阶、能力进阶。

四、任务驱动

问题的解决是以学习任务为载体来实际推动的。产生了数学问题，不等于就产生了能够驱动学生学习的推动力，这需要学习任务去驱动。实际上，在教师的教与学生的学之间横亘着一条条“鸿沟”，如学生应该达到的水平与实际水平的差距，教师想要教给学生的知识与学生实际接受水平的差距，教师教知识的方式方法与学生实际参与程度的差异等。因此，特定的学习任务要成为帮助学生跨越这些“鸿沟”的桥梁。但是，在某些数学课堂上，学习任务不能紧密结合学情，不能将数学学科核心素养与具体数学内容结合起来，学生不知道自己该做什么以及完成的标志是什么，任务往往缺乏连贯性，学生疲于应付各种学习任务，对于学习任务背后的数学方法与核心观点不能深入触及。深度学习视角下的任务驱动就是要基于数学问题解决的需要，结合真实情境，设计能够承载学习目标的核心任务，再结合学生的学习基础、学习习惯，将核心任务分解成若干个子任务。任务要具有挑战性、开放性、综合性和关联性，子任务间要进行结构化衔接，学生以完成可视化、共享化的学习成果为标志，在子任务完成过程中探索和解决数学问题，实现数学核心素养的发展。

如子问题串4对应的子任务的设置要以余弦定理的迁移应用为目标，让学生在不同情境中完成学习任务，在联系、加工、处理、转换过程中，实现要点弄通、多点联通、触类旁通。

1.在△ABC中，已知b=3，c=1，A=60°，求a。

2.在△ABC中，已知a=3，b=5，c=7，求cosB。

3.在△ABC中，已知a=3，b=5，c=7，求△ABC最大内角的余弦值。

4.在△ABC中，已知a=3，b=5，c=7，判断△ABC的形状。

5.在△ABC中，已知b=3，c=[23]，A=[[  6]]，解三角形。

6.在△ABC中，已知AB=9，BC=7，AC=8，求AC边上的中线长。

五、活动驱动

任务的完成需要在活动中实现。数学教学是活动的教学，这一点已经得到广大数学教师的认同。然而，在实际教学中很多教师会用学习的部分活动代替学生完整的学习活动，如让学生从教材中找相应的知识点进行填空来代替学生的自主学习，让学生通过小组合作、讨论交流、组长展示、总结点评来代替数学探究、数学创新活动，让个别学生的展示活动来代替全体学生的学习活动，用识记、理解、应用等低阶思维活动来代替分析、评价、创造等高阶思维活动等。学生的学习活动不能走过场，要避免标签化、简单化，要体现结构化、主体性、阶梯性。［4］深度学习视角下的活动驱动就是要基于学习任务的高质量完成，结合学习任务设计符合学生实际的学习活动，激发学生的主体参与意识，促使学生以主体的身份参与学习活动；设置完整的深度加工学习链条，激活学生学习的兴趣，引发认知冲突；引导学生建立知识间的关联，形成有效联结；在新的情境中迁移应用，解决新的问题；以批判性的眼光审视数学现象，进行辨别、辨析、辩论；模拟社会实践的真实情境，在应用情境中解决实际问题，并产生新的待探索的问题。由此，把握数学学科本质，培养“四基”，提升“四能”，实现“三会”，发展核心素养。

如为完成子问题串5的学习任务，学习活动的设计要充分发挥学生的主体性，让学生以余弦定理为支点撬动三角函数综合应用能力的提升。

【让学生说】你还能想到三角形中的哪些关系？（在三角形中大边对大角，任意两边之和大于第三边，内角和为180°，任意两个角的和小于180°等。）

【让学生想】如果a＞b，那么sinA与sinB、cosA与cosB的大小能确定吗？三角形的内角和定理在三角函数的化简中有什么作用？根据0＜A+B＜，能得到关于A、B的什么样的三角函数关系式？

【让学生写】你能转化出哪些可以定量计算的式子？［由a＞b推出cosA＜cosB，由sin（A+B）=sinC，cos（A+B）=-cosC，tan（A+B）=-tanC，0＜A+B＜，推出cosA+cosB＞0等。］

【让学生交流】这些结论从其他侧面反映了三角形中的边角关系，将这些定性问题转化为定量问题所依赖的数学思想方法是什么？（利用三角函数的单调性、诱导公式进行转化，体现了对应思想、函数思想、数形结合思想等。）

以上学习活动的开展，深化了三角形与三角函数的联系，同时为正弦定理的学习埋下伏笔，有助于新结论的发现，助推学生的思维由单点结构向多点结构进阶，由多点结构向关联结构、抽象拓展结构进阶。

六、评价驱动

教、学、评应该是一体化、一致的。教、學、评一体化是深度学习的内在要求与具体体现，是落实学科核心素养的关键。缺少了教学评价，教师的教就失去了灵魂与价值，学生的学就失去了意义与方向。［5］在有些课堂上，教、学、评一体化并没有真正落实好、实施好，关键原因是评价并没有真正发挥作用。教师只顾着教，学生只忙着学，评价与教、学割裂开来，评价的导向、诊断、调节、激励、管理、发展、甄别、鉴定等功能没有得到充分发挥，这样反而容易导致教师教得不深，学生学得不透。在评价主体上，往往注重教师的作用，而忽视学生自身、同伴、小组、班级、家长、社区、社会等主体的作用；在评价内容上，往往注重评价学生知识掌握的程度，而忽视对学生能力提升、情感体验、价值观念的评价；在评价方式上，往往注重教师点评，而忽视学生自评、同伴互评、小组评价、家长评价、社区评价等方式。深度学习视角下的评价驱动就是基于教、学、评的一致性，利用评价对学生产生积极促进和正强化，突出教学评价的多元化实施，同时要注重教师评价的提问方式、语言组织方式、交流工具、反馈方式的选择与使用，围绕数学主干知识、核心概念、核心问题、核心任务、中心活动，以一以贯之的评价指标开展持续性、一致性、全程性的教学评价。深度学习的评价强调过程性评价，突出数学思想方法、思维方法、研究方法、学科观念的连贯性，从而促进学生数学核心素养的阶段性、连续性发展。

为评价学生余弦定理的学习效果，可以设置如下评价活动，以此引导学生再一次审视余弦定理的来龙去脉，深层次揭示余弦定理的数学本质，引发学生对定性研究到定量研究的深度思考，激发学生的深层次学习思考与体验，促进学生主动求学、真学、深学、乐学。

1.请每位同学课后查阅相关资料，了解余弦定理的发展史，写成一个数学故事，在班级学习园地展示交流。

2.用不同的数学语言叙述余弦定理，并尝试用多种方法证明，写成数学小论文，并在班级进行展示分享。

3.思考“为什么不能用边边角判定三角形全等”，举出具体例子加以演算说明，并利用图形进行解释，小组内互评。

总之，深度学习需要驱动。观念、情境、问题、任务、活动、评价是深度学习驱动的核心要素，也是基于核心素养发展的课堂教学的重要抓手。深度学习从来都不是空的，深度学习的驱动更需要从教学中的每一个环节入手用心实施。

参考文献：

［1］刘月霞，郭华.  深度学习：走向核心素养［M］. 北京：教育科学出版社，2018：7.

［2］中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）［M］. 北京：人民教育出版社，2020：1.

［3］罗增儒.  数学素养课堂落实的思考［J］. 中小学课堂教学研究，2020（11）：3-6，31.

［4］郑金宾，郑成鸾，赵维亮.  以“任意角”为例看深度学习之“深”［J］. 中学数学杂志，2023（9）：31-34.

［5］张维忠，江漂.  素养导向的数学核心素养评价：《义务教育数学课程标准（2022年版）》的新变化［J］. 中小学课堂教学研究，2022（7）：1-3，7.

（责任编辑：潘安）