提升学生认知能力的数学教学探索
王琳 陈锋 夏马成

摘 要:针对2022年无锡市中考试题中一道常规代数推理题得分率偏低的情况,文章深入剖析了学生失分的原因,并进行了典型认知错误的分析,提出了一系列针对性的教学策略,包括研读课程标准与教材,夯实基础教学;参考教材力求规范,注重规范教学;注重学生能力培养,彰显核心素养。这些策略的实施将有助于提高学生的代数推理题得分率,进一步提升学生的整体学业水平。
关键词:试题剖析;认知分析;代数推理;数学教学
数学作为中考的重要科目之一,是考查学生逻辑思维、分析能力和问题解决能力的重要工具。其中,代数推理题是数学中考中常见的一类题型,它要求学生灵活运用所学的代数知识,通过推理、分析、计算等多种手段,找出问题的解决方案。
2022年无锡市中考试卷中第26题是一道比较常规的代数推理题,而且在平时教学中,教师都作为典型例题强调过,但实际得分情况却出乎意料,满分10分的题,平均得分只有4.09分。针对这一情况,文章深入剖析了学生失分的原因,并提出一系列针对性的教学策略,以期提高学生的代数推理题得分率。
一、中考试题剖析
(一)试题呈现
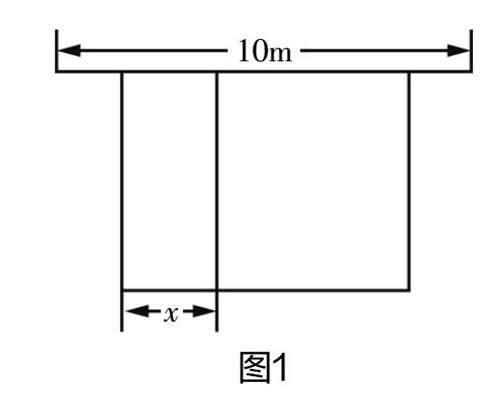
某农场计划建造一个矩形养殖场,为充分利用现有资源,该矩形养殖场一面靠墙(墙的长度为10m),另外三面用栅栏围成,中间再用栅栏把它分成两个面积为1∶2的矩形,已知栅栏的总长度为24m,设较小矩形的宽为xm,如图1所示。1. 若矩形养殖场的总面积为36m2,求此时x的值;2. 当x为多少时,矩形养殖场的总面积最大?最大值为多少?
(二)命题立意
纵观无锡市近几年中考数学试题的命题特点,最后三道压轴题中必有一道方程、不等式、函数相结合的应用题。今年在“双减”背景下,为了稳中求变,变中求新,命题组在该试题的命制过程中,始终围绕体现数学本质、凸显学生数学核心素养的宗旨,以便更好地体现本题所承载的选拔功能。《义务教育数学课程标准(2022版)》中的学段目标提到:第四学段(7-9年级)会用代数式、方程、不等式、函数等描述现实问题中的数量关系和变化规律,形成合适的运算思路解决问题;形成抽象能力、模型观念,进一步发展运算能力。在新课标的目标和理念的引领下,命题组遵循“源于教材,又高于教材”的原则,同时突出考查学生的阅读理解能力、自主探究能力,考查学生从数学的角度发现和提出问题、分析和解决问题的能力,从而落实学生的学科核心素养。
(三)素材选取
根据双向细目表和数学学科素养的要求,命题组选取了苏科版教材九年级上册第34页的习题10和11进行了改编。具体素材内容如第10题:学校打算用长16m的篱笆围成一个长方形的生物园饲养小兔,生物园的一面靠墙(如图2),面积是30m2,求这个生物园的长和宽。第11题:如图3,用长6m的铝合金条制成“日”字形窗框,窗框的宽和高各是多少时,窗户的透光面积为1.5m2(铝合金条的宽度不计)?
(四)试题评析
素材上的两道题解题思路一样,都是设宽为xm,然后用x表示另一条边,根据面积列方程求解。但是,从学生的解答过程来看,第11题的错误率会明显高于第10题,因为第11题中的“日”字形,多了一条宽,这也是学生思维上所遇到的一个障碍。因此,此次中考第26题就将这一“障碍”融入进去,导致接近10%的学生在这道题上失误了。另外,素材中的第10题,没有给出墙的长度。而在中考第26题中,墙的长度决定了最后解的取舍问题。有部分学生忽略了这个条件,也导致了失分。对比原题,“高于教材”就体现在了两个方面:第一,中间多了一道分隔栅栏;第二,墙的长度限定了x的取值范围。面对这样的问题,学生会有似曾相识的感觉,可以有效激发学生的探究欲望,促进学生的数学思考,提高思维的效率。该命题意在引领教师更加注重教材,创造性地运用教材;引领教师反思教学,树立以发展学生学科核心素养为导向的教学意识;引领教师改变教学方式,引导学生走上热爱数学,开发智慧的学科育人之路。
二、典型认知错误分析
(一)审题不够仔细,忽略重要条件
认知失误一:“中间再用栅栏把它分成两个面积为1∶2的矩形”这个条件没有注意,由面积1∶2的关系得到平行于墙的一边长为3xm,而垂直于墙的栅栏误以为2根,中间分隔的没有计算在内,错误地将垂直于墙的一边长表示为m。有这种失误的学生很多,大概要占10%。
认知失误二:“该矩形养殖场一面靠墙(墙的长度为10m)”这句话中括号里的一个隐藏条件没注意,学生忘记检验所求得的解是否符合题意。通过列方程可求得x有两个解2和6,而当x=6时,平行于墙的一边长为18m,大于了墙长,不符合题意,应舍去。
认知失误三:学生未注意“x为较小矩形的宽”这个条件,答题时根据面积1∶2进行了分类讨论。若左边与右边的面积比为1∶2,则平行于墙的一边表示为3xm;若左边与右边的面积比为2∶1,则平行于墙的一边表示为1.5xm。学生思考了两种情况,花了大量时间求解,却还被扣分。
(二)基本技能不足,计算频频出错
认知失误一:将所列方程去分母,化简为9x(24-3x)。此类学生想利用等式的性质,去掉左边式子上的分母3,两边同乘以3时,左式反而多乘了3。其实,没必要两边同乘以3,代数式化简掌握得好的学生,直接可以利用左边式子的因数3,直接进行约分化简。
认知失误二:一元二次方程求解不熟练。对方程x2-8x+12=0不会用十字相乘法求解。有的学生用公式法求解,在代公式时,计算出错。有的学生用配方法求解,配方出错,或是直接开方时出错。
认知失误三:有学生设垂直于墙的一边长为ym,从而列出了方程组x+y=8
xy=12,不会消元求解,只会用整数去凑解。
(三)函數思想欠缺,性质理解不透
第2题“当x为多少时,矩形养殖场的总面积最大?最大值为多少?”这道题是借助函数思想,建立面积S与x的函数关系式,由函数的性质来求得面积的最大值。
认知失误一:部分学生不考虑自变量x的取值范围,直接根据函数表达式S=-3(x-4)2+48得当x=4时,S最大=48。
认知失误二:二次函数的增减性不会描述。如“∵-3<0,∴S随x的增大而减小”,这与一次函数的增减性混淆。“∵-3<0,∴S随(x-4)2增大而减小”“S随x-4增大而减小”“x越接近4,S的值越大……”虽说有一定的道理,但是并不规范。
认知失误三:不理解函数的连续性,或者说自变量的范围。例如,“∵0 三、改进课堂教学的策略 (一)研读课程标准与教材,夯实基础教学 《义务教育数学课程标准(2022版)》的修订原则是坚持目标导向、坚持问题导向、坚持创新导向,对教学增强了指导性。各课程标准针对内容要求提出学业要求、教学提示,细化了评价与考试命题建议,注重实现“教—学—评”一致性,增加了教学、评价案例,不仅明确了“为什么教”“教什么”“教到什么程度”,而且强化了“怎么教”的具体指导。所以每位教师都需要仔细研读新课标和教材,紧扣课程标准和教材来制订教学目标,夯实基础是重中之重。尤其是在面对中考的初三复习课时,教师往往把题目的难度拔得很高,而忽视了最根本的基础教学。此外,很多教师在实际教学中固守传统的教学模式、教学理念。有些教师虽然能够学习、了解课程标准,但对课程标准的理解仅停留在基础层面,并未对其实际的内涵进行深入挖掘。 例如,部分学生在解题过程中,因解方程计算出错的频率很高,但试题中的计算量并不大。一元二次方程的解法、方程组的消元法等都是课标中要求必须掌握的。作为一线教师,在课堂教学过程中,必须重视“四基”,在基础教育时需要舍得花时间,让学生慢慢去理解,去悟透,而不要急于求成。比如,教师在教授解方程中的去分母时,不是看到有分母就机械性地立即去,而是先引导学生观察式子能否先化简,化简后如果有分母再考虑去分母。无论是解方程还是计算,教师都得让学生放慢速度,先观察思考,再用最优的方案去解决问题。 (二)参考教材力求规范,注重规范教学 数学课程要培养学生的核心素养,主要包括三个方面:第一,会用数学的眼光观察现实世界;第二,会用数学的思维思考现实世界;第三,会用数学的语言表达现实世界。数学的眼光是抽象敏锐的,数学的思维是逻辑严谨的,数学的语言是精准简洁的。因此,数学教师在数学课堂上除了强调解题方法外,还需关注学生数学语言的表达是否有逻辑、是否严谨、是否规范。从阅卷工作中可以发现,由于书写不规范导致失分的情况也很普遍。作为教师得反思,平时的教学是否规范,日常的课堂语言、板书示范、学生作业的修改,教师都要参考教材,力求规范。数学是一门非常讲究严谨的学科,教师应在平时的教學中渗透这种思想,注重培养学生的规范意识,让学生在学习过程中逐步养成良好的学习习惯。 (三)注重学生能力培养,彰显核心素养 学生核心素养的养成,不是靠教师课堂上“教”出来的,而是要学生主动参与课堂上的数学活动来获取的;不是让学生成为“解题模仿机器”就能培养出来的,而是需要学生自己去感悟与思维的;不是通过强化训练突击出来的,而是学生经过思考后日积月累攒下来的。教师在教学时往往存在“轻过程、重结果”的错误做法:一是新授内容无限制地被压缩,相关概念、原理等新知内容,课上一带而过,甚至和盘托出;二是进行大规模机械重复的强化训练,并加大训练难度,导致学生在数学学习过程中出现了这样一种奇怪的现象:虽然不知道问题是如何产生的,却知道如何去解答,“知其然而不知其所以然”几乎成了许多学生数学学习的真实写照。 例如,从这次中考的第26题答题情况来看,学生在审题不仔细上失分的情况严重。因此,教师在教学过程中不仅要教授解题方法,还应该引导学生如何去读题、如何去分析题目,让学生自己思考,最终获得最优化的解题方案。本次中考的第26题也是旨在引导教师要关注学生自主学习、主动探究的学习方式,试题“模仿式”的教学是无法提升学生探究能力和发展学生思维的。因此,教师要执果索因,不断反思、优化课堂,做到从传授知识到传授思维,由“授人以鱼”转变为“授人以渔”。数学学习离不开解题,掌握数学思想方法,才能站在解题的制高点。在教学中,教师应把数学思想方法渗透每一堂课中,通过“一题多解”或“一题多变”,让学生在多元思维碰撞中,感悟与形成思想方法。 综上所述,深入剖析学生在考试中的失分情况,有助于教师明确课堂教学中的薄弱环节,并为今后的教学工作提供改进方向。中考答卷不仅考察了学生对知识的掌握程度,还展现了学生的综合素质和学科能力。因此,教师在教育教学过程中,应当聚焦于理解、思维、思想方法和数学精神的培养,应潜移默化地在课堂上实现知识与能力的融合、方法与实践的结合、教书与育人的统一,从而实现学生全面发展。 参考文献: [1]秦奋. 由一道题的解答失误谈中考几何复习[J]. 中学数学教学参考,2020(14):46-48. [2]林崇德. 学生发展核心素养:面向未来应该培养怎样的人?[J]. 中国教育学刊,2016(06):1-2. [3]张月媚. 提升学生数学能力的一种教学模式探索[J]. 福建教育学院学报,2008(06):123-125. (责任编辑:淳 洁)

