思维导图在初中数学教学中的应用研究
李会梅
【摘要】数学是一门培养学生推理能力和逻辑思维的学科,在学生的学习生涯中占有极其重要的地位.而思维导图是一种常见的整合信息和梳理信息的工具,能够围绕中心思维向外生发出成千上万个关联项目和数学知识,最终使得某一数学概念呈现立体式、放射性的思维结构.因此,在初中数学教学过程中,教师可以借助思维导图将文字和图形以及所学知识用相互关联和隶属的层次关系加以表示,进而强化学生的数学思维,提高学生的学习效果.鉴于此,文章简析了目前教师在初中数学教学中使用思维导图时存在的问题,并从思维导图在初中数学教学中的应用价值出发,结合笔者自身的教学实践,探索出一些思维导图在初中数学教学中的应用策略,以供参考.
【关键词】思维导图;初中数学;课堂教学;应用策略
引 言
在升入初中后,数学学科的学习难度明显增加,且此阶段的数学知识多以代数、几何为主,这意味着学生会学习大量的概念、公式以及定理等抽象性知识.这就要求学生具备良好的分析能力以及逻辑思维能力,以攻克初中阶段的数学难题.随着教学改革的不断深化,数学学习不再是单一的课堂教学,学生也不再是机械化的“考试机器”,因此教师要在关注学生学习成绩的基础上,培养学生数学核心素养,优化学生的数学思维,引导学生在分析问题、解决问题的过程中,将习得的数学知识转换为数学技能.因此,数学教师有效利用“思维导图”这一教学工具能够切实提高学生的数学学习效率和课堂数学的成效.
一、思维导图的概念简述
思维导图又名“思维地图”或“脑力激荡图”,最早是由英国著名心理学家东尼·博赞发明的一种表达发散性思维的有效图形思维工具.它的出现与发明离不开人类的发散性思维方式.作为一种图文并茂式的思考工具,思维导图能借助鲜明的树状结构,将多个知识和概念加以连接,从而借助层次分明的层级图展示不同内容之间的隶属关系,进而梳理出多个概念之间错综复杂的内在联系.由此可知,思维导图最大的特点有两个方面,即图文并茂和结构鲜明.图文并茂的特点能够帮助学生更好地建立形象思维,且文字大多是精炼的关键语句,有助于学生识记;而结构鲜明的特点可有效优化学生的整合性思维和发散性思维,从而使学生建立清晰的学习思路.
二、初中数学教师在使用思维导图时存在的问题
(一)弃之不用———教师思想传统,教学理念落后
在很长一段时间内,受传统教学理念的影响,很多教师,尤其是老教师不愿意接受新兴思想,更不愿主动地探索和运用新的教学理念.因此,很多时候的数学课堂内容十分单薄、枯燥.思维导图作为一种新型的教学方式,很多数学教师对它有一种抵触心理,认为它只能应用于文科教学当中,在理科教学,尤其是数学教学中的应用少之又少.这样一来就极大地缩小了思维导图在数学教学中的使用范围.
(二)流于表面———过分关注形式,反而忽视内容
部分数学教师注意到了思维导图对数学教学的助力作用,也在自己的教学过程中有意识地应用了思维导图,但是由于自身能力的局限,其没能有效创新思维导图的使用方法,只是僵化地生搬硬套,只考虑自己班级的基础学情和学生的实际情况,使得思维导图的使用和学生数学核心素养的提升成为互不相干的两大部分.长此以往,既丧失了教师的教学热情,又消磨了学生的参与兴趣,最终难以体现思维导图在数学学科中的教学价值和教学作用.
(三)故步自封———导图结构单一,实施形式僵化
思维导图的适用范围十分广泛,不仅可以用来整合、归纳数学概念和知识点,还可以强化学生的迁移性思维,串联相似题型;不仅能引导学生梳理解题的思路,还能强化学生的知识网络.但是部分教师对思维导图的适用范围认知不清,觉得思维导图只能用来整理相应的数学概念以避免学生混淆,殊不知思维导图的应用形式多种多样.这样僵化的实施方式使得思维导图在数学教学中难以发挥应有的作用.
三、思维导图在初中数学教学中的应用价值
(一)简化知识内容、整合数学概念的有效工具
因为思维导图讲求图文并茂,而其中的文字都是精炼的关键语句,所以教师借助思维导图能够更好地帮助学生简化繁杂的数学概念和理论知识,精取其中的关键要素加以理解和记忆.同样,在深入理解和制作思维导图的过程中,学生通过对知识脉络的横向及纵向对比,可前后联系,触类旁通,进而实现举一反三.因此,在这一过程中,学生能够迅速建立起全面且完整的数学学习网络.
(二)发散数学思维、攻克教学难点的关键举措
思维导图本身就是基于人类的发散性思维而进行总结和分析的,因此学生会在制作思维导图的过程中探索知识点之间的联系,并在实践中逐渐深化对知识的理解,进而提高知识的综合應用能力.这样可使学生根据自己的学习需求对思维导图进行制作或优化,使其整合性思维和分类性思维得到很好的锻炼和发展,最终达到发散学生数学思维的目的,更好地引导学生攻克数学学习中的难点问题.
(三)深化知识理解、提高自学能力的核心做法
思维导图的图文并茂形式能为学生直观地呈现知识点之间的联系,使学生能够找到容易掌握的记忆点和不容易区分的混淆点.同样,教师引导学生自行制作思维导图,能够使学生自觉发现知识点之间的联系,串联新旧内容,从而辅助自己更好地理解数学知识,进而实现提高学生自学能力的教学目标.
四、思维导图在初中数学教学中的实践
(一)预学:借思维导图辅助学生预习,奠定课堂学习基础
课前预习是学生养成良好学习习惯的关键阶段.良好的课前预习能提高学生在数学课堂上的学习效率.教师借助思维导图辅助学生进行课前预习,能够创新课前学习形式,激发学生的学习兴趣.因此,教师不仅可以让学生在完善思维导图的过程中完成预习作业,还可以让学生根据自己提前给出的思维导图理清容易混淆的知识点,优化课前预习效果.
以人教版初中数学七年级上册“正数和负数”的教学为例,本节课意在让学生理清正数和负数的概念,学会用正数、负数表示意义相反的量,理解“0”的意义.教师可提前准备一个包含关键概念的初步思维导图,如以“有理数”为中心词,以“正数”“负数”“整数”“分数”“零”为分支.这个思维导图可以包括一些关键词,但要留有空白供学生自行填写.
1.布置预习作业
教师布置预习作业,让学生基于自己给出的基础思维导图,通过课本或其他资源填补空缺部分,如例子、性质和其在日常生活中的应用等.比如,在“正数”分支下,学生需要找到并填写正数的定义、性质及其在生活中的例子(如温度上升)等;在“负数”分支下,学生需要填写负数的相应信息;在“零”的分支下,学生需要描述它的特性和意义.
2.学生自主学习
学生利用课本和其他资源独立完成思维导图的补充工作.在这个过程中,学生可以自己手绘或用电子设备完成思维导图,同时要在思维导图中用自己的语言解释概念,从而加深对知识的理解与记忆.
3.互动交流
学生独自完成思维导图后,可以通过小组讨论的方式互相检查,从而补充彼此的思维导图,这样可以更深入地探讨每个概念.教师也可以组织一个小组讨论会,让学生展示并解释自己的思维导图,这样可以帮助其他学生从不同的角度理解数学概念.
4.课堂教学衔接
在正式开始上课之前,教师可以选取几个优秀的思维导图,和全班学生一起分析和讨论,从而让所有学生都能看到多元化的思考方式.教师可以根据学生提交的思维导图,了解学生的预习情况,并在课堂上针对学生普遍存在的问题进行详细解释.教师可以给出一个简单的思维导图模板,引导学生借鉴、理解,之后让学生根据自己的学习经验和预习情况完成一个属于自己的“有理数”思维导图,进而为课堂学习奠定基础.
(二)导学:借思维导图强化课堂笔记,归类细化课堂知识
不同于传统的文科学习,数学知识更加细碎化和零散化,因此很多时候学生很难有条理地记录数学笔记.因此,教师可以借助思维导图引导学生条理清晰地记录课堂笔记.这样一来,大框架的课堂知识会更加精细,而细碎化的知识结构会更加明确.
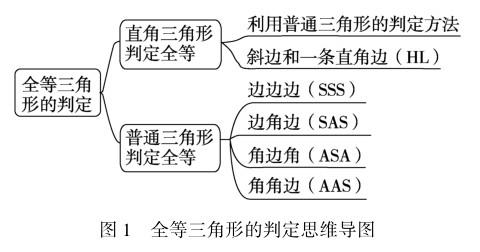
以人教版初中数学八年级上册“三角形全等的判定”教学为例,本部分内容繁杂众多,学生在记笔记时会出现毫无头绪的情况,此时教师可以引导学生借助思维导图快速地完成笔记记录.例如,在判定全等三角形的方法中,普通三角形和直角三角形是有所区别的.因此,在这里,教师可以引导学生以“全等三角形的判定”为中心词,延伸出同级隶属关系的“直角三角形判定全等”和“普通三角形判定全等”.直角三角形的全等判断方法可延伸出两大分支,第一分支是利用普通三角形的判定方法,第二分支是直角三角形的特殊判定方法,即“斜边和一条直角边(HL)”.同样,普通三角形的全等判断方法可扩展为四种,即“边边边(SSS)”“边角边(SAS)”“角边角(ASA)”“角角边(AAS)”.
(三)活学:借思维导图扩展解题思路,培养学生数学发散思维
数学讲求活学活用.因此,数学教师借助思维导图能够使学生建立起解决数学问题的多元视角,进而使学生能够运用多种路径解决数学问题,拓展学生的解题思路,同时有利于学生进行知识点之间的迁移,使学生在梳理某一知识点的思维导图时,可以发散到另一相似知识点中,进而发展学生的思维品质.
一般情况下,学生在解答几何题目时,会因所做的辅助线不同,而使最终形成的解题思路也有所不同.因此,教师可以让学生将自己的解题思路进行整理,并借助思维导图的方式加以呈现.例如,学生可将例题作为思维导图的依据,将“辅助线”确定为中心点,并延伸出多个下级隶属关系,以此说明做辅助线的不同方法以及做辅助线的目的,进而不断扩展解题思路.学生将同一题目的多种方法以思维导图的形式加以呈现,既可培养发散性思维,又可选出最优解法.
(四)用学:借思维导图联系实际生活,提高学生核心素养
《义务教育数学课程标准(2022年版)》对数学核心素养有明确规定,即要求学生“会用数学的眼光观察现实世界,会用数学的思维思考现实世界,会用数学的语言表达现实世界”.因此,教师可以引导学生运用数学思维导图看待问题,解决问题,进而实现学以致用、知行合一的教学目标,最终提升学生的核心素养.
以人教版初中数学七年级下册“平面直角坐标系”教学为例,教师在教学过程中可以一边展现思维导图的内容,一边以班级为模板,将坐标系中的位置表示与学生的实际座位进行联系.比如,在以“平面直角坐标系”为中心词进行延伸时,下级隶属两个分支,即“概念”和“象限”,此时教师可以以班级为模板,确定座位中心的学生即为原点位置,随后根据他的座位和坐标系的概念确定横纵轴以及方向.接着,教师在介紹“象限”这一内容时,可以让处于第一象限的学生暂时起立,随后按顺序逐一起立,引导学生建立思维导图和现实生活的联系,更好地帮助学生理解数学概念,同时为接下来利用平面直角坐标系表示地理位置的学习奠定基础,降低难度.
结 语
初中阶段是学生学习数学知识、培养数学能力的关键时期.为了帮助学生更好地学习数学知识,数学教师应及时更新教学理念,优化教学方法.数学教师借助思维导图,可有效培养学生的核心素养,提高学生的学习能力,激发学生的学习兴趣和探究热情,进而推动数学课堂的进步与发展.数学教师要巧用思维导图助力课堂进步,促进学生的能力提升和素养发展.
【参考文献】
[1]刘娜.思维导图在初中数学教学中的运用探究[J].教育艺术,2023(3):75.
[2]魏禄山.思维导图在初中数学教学中的应用[J].数学学习与研究,2023(4):26-28.
[3]邵前进.浅议思维导图在初中数学教学中的作用[J].课程教育研究,2018(39):123.
[4]张德礼.“思维导图”助力初中数学难点学习[J].学周刊,2019(12):98.
[5]陈春花.核心素养下思维导图在初中数学教学中的应用[J].新课程教学(电子版),2023(1):7-8.
[6]曾伟,黄泳.“思维导图”助力初中数学难点学习[J].学周刊,2017(1):107-108.

