一种基于多层次校验的低恢复成本纠删码
邓文杰 洪铁原 唐聃 王燮


摘 要:随着纠删码在分布式存储系统中的实际应用,纠删码为存储系统提供了更加优秀的存储效率,但当节点丢失时,相较于传统副本技术更多的网络传输带宽开销成为了造成系统性能瓶颈的关键因素。为了解决MDS编码高带宽开销对系统性能的影响,一类新型编码方案——分组码被应用在分布式存储系统中,相较于传统MDS编码能够有效地降低节点修复时的数据传输量,从而减少网络带宽需求。在Pyramid分组码的基础上进行层次扩展,提出一种HLRC(hierarchical local repair codes)纠删码。HLRC相较于LRC引入了层次编码模型,将原始数据块构建为编码矩阵,根据层次进行分别编码,生成包含数据块范围不同的局部校验块;每个层次包含的数据块数量不同,可以保证修复节点时的低修复成本,同时还拥有较高的存储效率。HLRC相较于Pyramid拥有额外的校验块冗余,能够降低校验块出错和多节点出错时的恢复开销。在基于Ceph的分布式存储系统中的实验结果表明,HLRC与Pyramid等分组码相比,单节点修复开销最高可降低48.56%,多节点修复开销最高可降低25%。
关键词:纠删码;分组码;层次编码;带宽开销;恢复成本
中图分类号:TP391 文献标志码:A 文章编号:1001-3695(2024)05-023-1441-07
doi: 10.19734/j.issn.1001-3695.2023.08.0399
Low recovery-overhead erasure codes based on multi-hierarchical check
Abstract:With the practical application of erasure codes in distributed storage systems, erasure codes provide better storage efficiency for storage systems, but when nodes are lost, more network transmission bandwidth overhead compared with traditional replica technology becomes a key factor causing system performance bottlenecks. In order to solve the impact of high bandwidth overhead of MDS coding on system performance, a new type of coding scheme, packet coding, is applied in distri-buted storage systems. Compared with traditional MDS coding, it can effectively reduce the amount of data transmission during node repairing, thus reducing the network bandwidth demand. This paper proposed a HLRC(hierarchical local repair codes) based on the hierarchical expansion of Pyramid codes. HLRC introduced a hierarchical coding model compared to LRC, which constructed the original data blocks as a coding matrix, and coded according to the hierarchical levels to generate local checksum blocks with different ranges of data blocks. Each hierarchy contained a different number of data blocks, which ensured low repair cost and high storage efficiency when repairing nodes. HLRC had additional checksum block redundancy compared to Pyramid codes, which reduced the recovery overhead in the event of checksum block errors and multi-node errors. Experimental results in a Ceph-based distributed storage system show that HLRC can reduce single-node repair overhead by up to 48.56% and multi-node repair overhead by up to 25% compared to Pyramid codes and other packet codes.
Key words:erasure code; group repair codes; hierarchical coding; bandwidth overhead; recovery overhead
0 引言
在當今数字化时代,海量数据的存储和处理已经成为一项重要且具有挑战性的任务。分布式存储系统[1~3]作为一种有效的数据管理和存储方案,被广泛应用于云计算、大数据分析和分布式计算等领域。然而,这些系统面临着诸多挑战,如节点故障、网络延迟和数据丢失等。
纠删码(erasure code)[4]是一种高效的冗余编码方案,用于在分布式存储系统中实现数据的冗余和容错。与传统的副本技术[5]不同,纠删码可以通过增加冗余数据,以较低的存储代价提供更强的容错能力。在分布式存储系统中,数据通常会被划分为多个数据块,并分布存储在不同的节点上,以实现数据的冗余备份和高可靠性。当某个节点发生故障或数据丢失时,纠删码可以通过冗余数据恢复丢失的数据块,而无须访问原始数据所在的节点。这种冗余和恢复的能力使得分布式存储系统能更好地应对节点故障、数据丢失等问题。
具备MDS性质的RS码[6]等纠删码拥有理论最优的存储效率,同时能够提供较好的容错能力,但缺点在于节点出错进行数据恢复时对网络带宽的占用过高。在分布式存储系统中,由于其易扩展的特性,网络带宽相较于存储空间而言更为珍贵,所以此类编码很容易造成系统性能的瓶颈[7]。
阵列码作为纠删码的另外一个分支,其主要思想是将条带内的数据块生成一个编码阵列,通过阵列进行编码生成校验块。其优点是计算简单,且在以节点为出错单位时,大部分的阵列码都为MDS编码。现阶段主流的阵列码有EVENODD码[8]、DRDP码[9]等。相较于传统MDS编码,其编译码都是基于简单的XOR操作,所以计算简单且高效,编译码过程也易于实现。但是依然存在传统MDS编码的缺点,在节点出错时需要读取的数据量非常大,对网络带宽造成相当大的挑战,容易引起系统的性能瓶颈。同时LDPC[10]编码方案采用了图结构进行编码,修复开销优秀,但其基于Tanner图和概率的构造方式使其更适合在信道编码中使用。Tu等人[11]提出的DDUC码实现了更新和解码的解耦,从而提高了系统的并发性能;Zhang等人[12]提出的SA-RSR算法能够加速异或类纠删码单节点故障恢复。
根据现阶段研究表明,分布式存储系统中90%以上的节点丢失为单节点丢失[13],同时为了应对节点修复时网络带宽占用高这一挑战,研究人员提出了许多解决方案,其中之一就是分组码。分组码作为一种纠删码方案,具有在分布式存储系统中提供高可靠性和高效性的潜力。分组码的主要思想是将数据块分成多个组,并为每个组计算冗余信息,以实现错误检测和纠正。与MDS码相比,在面临节点故障时具备较低的修复成本。现阶段主流的分组码有LRC[14]、Pyramid码[15]、DLRC[16]、TLRC[17]等。其中,LRC最先提出将数据块分组,通过分组编码的思想降低单节点修复时需要读取的节点数目,从而大幅降低修复时的带宽需求;Pyramid码提供了多层次的分组编码思想,将局部校验块的类别按照实际需要来进行调整,更能够适应不同大小的存储系统需要;DLRC提出重叠编码的思想,让数据块分组时,不同的组内包含的数据块可以有一定的重叠,使得存储效率有较大提升;TLRC将全局校验块和数据块一起纳入到局部校验块的生成过程中,使得全局校驗块丢失时修复成本也较低。之后又提出了多种基于交叉编码的分组码,例如,SHEC[18]虽然容错能力优秀,但修复开销较大;GRC[19]采用将条带分组并增加局部校验块的思想来降低多节点修复开销;RGRC[20]通过旋转编码的编码方式将多个条带组合成条带集,进而减少修复成本。
分布式存储系统相较于传统集中式存储系统需要进行更多的数据迁移,现阶段主流的MDS纠删码方案在修复数据时需要较大的网络带宽开销,导致网络带宽经常成为系统性能的瓶颈,同时在分布式存储系统中大部分的节点丢失是单节点丢失。目前的纠删码方案研究仅限于修复开销和存储效率,对于同时提高单节点修复效率和存储效率的研究较少。针对以上问题,本文结合阵列码的阵列化思想提出层次局部修复码HLRC(hierarchical local repair codes)。其主要的思想是在编码时将数据块和全局块进行阵列化,通过编码阵列生成不同层次的局部校验块,在保证优秀的单节点修复性能的同时,为系统提供可观的容错能力,在分布式存储系统之中有良好的使用前景。
1 相关工作
1.1 RS编码
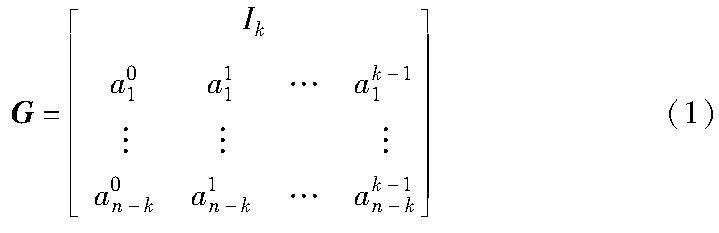
RS(n,k)码是一种具备MDS性质的编码,其计算都在GF(2w)上完成,主要思想是将文件拆分成数据块再进行条带化,每个条带内包含k个数据块D=(d1,d2,…,dk),通过与生成矩阵G相乘即可得到编译后的码字c=(c1,c2,…,cn),其中前k位为数据位,所以其为系统MDS码。生成矩阵的构造如式(1)所示,其中a为GF(2w)的元素。
当数据丢失时,只要丢失节点数x满足条件1≤x≤n-k,无论丢失多少节点数都可以通过读取所有的剩余数据块来进行修复操作,所以容错能力高但修复效率较为低下。
1.2 Pyramid编码
Pyramid(n,k)最先提出层次结构编码思想,其主要思想是将数据块划分为不同的层次,为每个不同的层次生成不同类型的局部校验块,所以可以更灵活地调整编码方案。图1展示了Pyramid(20,12)的编码结构。
其中每个校验块的生成都是基于MDS编码,在本文中MDS编码一般指RS码。图中Pyramid编码将数据块划分为三层次,第一层长度为3,第二层长度为6,第三层为全局校验块。用di代表当前条带内第i个数据块,pi表示当前条带内第i个子局部校验块,p′i表示当前条带内第i个局部校验块,p″i表示当前条带内第i个全局校验块。pi、p′i、p″i的构造方式如式(2)~(4)所示,其中r为全局校验块个数,li为第i层分组的分组个数。
Pyramid码的层次结构使其能够在拥有优秀的单节点修复开销的同时还兼顾一定的存储效率,但其缺点在于所有的全局校验块以及高层次校验块都没有添加额外的冗余手段,导致其多节容错能力不足,同时当丢失全局校验块或者高层次校验块时修复成本依然很高。
2 HLRC的设计
2.1 HLRC基础概念
本节对HLRC涉及使用的相关符号进行解释,其中HLRC(k, c, m, r, s)使用的符号具体含义如表1所示。
为了更好进行描述,本文定义以下概念:
定义1 编码阵列。将当前条带的数据块进行阵列化后的数据布局。
定义2 效率优先局部校验块。当前的编码阵列中第一层级的局部校验块,与Pyramid码类似,HLRC编码时也会产生不同层级的局部校验块,其中层级越低,编码组内的数据块越少。
定义3 存储优先局部校验块。当前的编码阵列中第二层级的局部校验块,其编码时组内数据块相较于第一层范围更广,存储效率也就更高。
定义4 校验全局校验块。当前条带中编码范围为所有局部校验块的校验块,其作用是为局部校验块提供额外的容错,能够为编码方案提供更好的容错能力和多节点修复性能。
定义5 数据全局校验块。编码矩阵中编码范围涵盖所有数据块的校验块,其主要作用是满足编码的容错性能需要。
定义6 修复成本。在本文中如没有特别指定,修复成本通常指定为节点恢复时读取和传输的总数据量。
2.2 HLRC编码
编码流程一般分为四个步骤,分别对应的是四个不同类型的校验块的生成。首先是数据全局校验块的生成,对条带内k个数据块进行编码操作,生成r个数据全局校验块,其中各个参数需要满足k+r+c≤c2。
a)进行数据全局校验块p=(p1,p2,…pr)的生成。定义矩阵GGlobal是一个r×k阶矩阵,其构造如式(5)所示;同时在所有校验块的编码中,a为GF(2w)上的元素,其构造方式如式(6)所示,其中任意两个g互异,且后续的构造方式也与a(i, j)构造方式一致。
通过GGlobal可以计算得到对应的数据全局校验块p,具体的计算流程如式(7)所示。
b)进行效率优先局部校验块p′=(p′1,p′2,…,p′c)的生成。定义矩阵GEF是一个c×m阶矩阵,构造如式(8)所示。数据矩阵DEF是一个m×c阶矩阵,其中di, j代表编码阵列中位于第i行第j列的数据块,构造如式(9)(10)所示。
通过GEF计算可以得到包含c个效率优先局部校验块p′的矩阵,取对角线元素即可得到c个效率优先局部校验块,计算流程如式(11)所示。
c)进行存储优先局部校验块p″=(p″1,p″2,…,p″m)的生成。定义矩阵GSF是一个m×c阶矩阵,数据矩阵DSF是一个c×m阶的矩阵,如式(12)~(14)所示。
通过GPGlobal计算可以得到m个存储优先局部校验块p″。
d)对于校验全局校验块p可以通过式(15)计算。
2.3 HLRC解码
HLRC的解码方式主要与丢失节点的数量与参与解码的校验块有关,可以根据丢失节点的数量将错误分为两类丢失错误:单节点丢失和丢失节点数大于1的多节点丢失。其中单节点修复拥有三种解码方法:效率优先解码、容错优先解码和校验块解码,其分别对应着三类不同校验块参与解码的方式。
2.3.1 单节点修复
对于单节点出错,若出错节点derrorp″,derrorp,设出错节点位于原编码阵列中第n行第j列,且不属于存储优先局部校验块。则可使用其对应的效率优先局部校验块分组内的数据进行解码,可以以最优的解码效率尽可能快速高效地修复错误。这类解码方式称为效率优先解码,如图2所示,具体修复步骤如下:
a)确定丢失节点所对应的效率优先局部校验块p′j。
b)得到p′j的编码方程,如式(16)所示。
c)通过p′j的编码方程以及组内的数据块,通过式(17)进行解码,得到丢失节点derror。
a)确定丢失节点在原编码阵列中对应的局部校验块p″n。
b)按照式(18)确定p″n的原编码方程。
c)通过p″j的编码方程以及组内的数据块,通过式(19)进行解码,得到丢失节点derror。
若出错节点为derror∈(p′∪p″∪p),即出错节点为任意一个局部校验块,则可使用其对应的校验全局校验块分组内的数据进行解码。这一流程被称为校验块解码,如图4所示,具体步骤如下:
a)确定丢失节点在原编码阵列中对应的第x个校验全局校验块px。
b)按照式(20)确定px的原编码方程。
c)通过px的编码方程以及组内的数据块,通过式(21)(22)进行解码,得到丢失节点derror。
表2为LRC(k,l,r)、DLRC(k,m,n,l)、HLRC(k,c,m,r,s)以及TLRC(k,m,s,x,r)的理论单节点修复开销。
2.3.2 多节点修复
定理1 设丢失节点个数为x,当拥有x个与丢失的数据块有关联的校验块时则能够修复该错误。
证明 当拥有x个校验块,意味着能够生成x个带有未知块数据的校驗方程。在2.2节编码时,每一个校验块生成时的生成矩阵内的gi都是两两互异的,且每一组方程的构成都按照RS码编码流程。所以在足够大的GF(2w)中,条带内每一个校验方程之间都是线性无关的。将x个校验方程组成校验方程组可以得到线性方程组Ax=b,由于每一个校验方程线性两两无关,可以推出系数矩阵A为满秩,则Ax=b的秩满足以下条件:r(A)=r(A,b)=x,线性方程组能够得到一个唯一解,则该错误可以修复。
本文提出一种效率最优的多节点修复算法,其基本思想就是首先使用修复开销最低的效率优先单节点修复算法来修复丢失节点中可以直接被修复的节点;再添加剩余节点的效率优先局部校验块编码方程至解码方程组;然后添加其他相关编码方程直至满足定理1中的解码条件r(A)=r(A,b)=x;最后联立方程组进行解码,即可实现修复开销最低的多节点修复。具体流程如图5所示。
下面以HLRC(11,4,3,1,1)为例来展示其编码过程,单节点修复过程以及效率最优多节点修复算法的执行过程。HLRC(11,4,3,1,1)的布局如图6所示。
通过本章的HLRC编码算法可以计算得到所有校验块,总体的生成矩阵G如式(23)所示。
通过图6可以看出,对于每一部分的校验块而言,其计算复杂度以及需要的数据块都不同。效率优先局部校验块拥有最优秀的计算性能,其计算只需要三个数据块,在保证少数节点可靠性的同时拥有优秀的修复性能。对于存储优先校验块而言,其拥有较效率优先校验块更优秀的容错性能,仅需四个额外的冗余空间即可为所有数据块提供容错,所以它能在效率优先校验块无法恢复错误时提供额外的辅助。全局校验块和校验全局校验块分别为所有数据块和所有局部校验块提供最基础的容错能力。
对于单节点出错,若出错节点derrorp″,derrorp,例如此处出错节点为d1,1,则优先使用效率优先修复,通过局部校验块p′1的修复方程,只需读取d2,1、d3,1、p′1三个节点数据即可恢复丢失节点d1,1。此类型错误修复代价最小,且占总单节点错误概率的80%。若出错节点derror∈p″,例如此处假设出错节点为p″1,则优先使用存储优先解码,通过存储优先局部校验块p″1的修复方程,只需读取d1,1、d1,2、d1,3、d1,4节点数据即可恢复丢失节点p″1。此类型错误修复代价更大,但只占总单节点错误概率的15%。若出错节点为derror∈p,则需要通过所有局部校验块联立进行解码,是修复代价最高的单节点错误。但由于其个数较少,只占总概率的5%,所以其高代价可以被忽略。
对于多节点出错,则按照效率最优的多节点修复算法的流程对其进行修复。设出错节点为d1,1、d1,2、d1,3、d2,1、d2,2、d2,3,则算法开始寻找每一个节点修复性能最高的效率优先校验块p′1、p′2、p′3。再寻找每个节点对应的存储优先校验块p″1、p″2,最后使用数据全局校验块p1。一共可以得到六个线性无关的编码方程,通过定理1判定后即可修复该多节点错误。
3 实验结果
本文实验主要在基于Ceph的分布式纠删码测试平台上对HLRC以及其他纠删码进行部署并进行相关的性能比较,以便能够得到最真实的实验结果。
3.1 实验环境
Ceph是一个大型可靠的分布式存储系统,本纠删码测试实验平台基于Ceph的Pacific(16.2.13)版本搭建,其主要构件有Monitor和OSD。OSD为数据节点,负责存放数据以及数据的管理,其中分为Primary OSD主数据节点和OSD普通数据节点,系统基于其现有框架进行扩展纠删码OSD来添加不同的纠删码方案。Monitor负责管理数据节点以及与客户端交互,具体结构如图7所示。
在图7所示的分布式实验平台上,对HLRC(k, c, m, r, s)算法进行了实现与应用,其具体的实现流程如下:a)在分布式存储系统之中将目标文件拆分为若干个条带,每个条带内包含k个数据块,通过2.2节的编码算法得到(c+m+r+s)个校验块;b)将条带内每个数据块依次放置在节点之中,具体的数据布局如图8所示;c)循环步骤a)b)直到目标文件编码完毕;d)当系统出现节点失效时,通过2.3节的解码算法得到最优的解码方案,通过条带内其他校验块的辅助,计算得到丢失数据块,循环步骤d)直到丢失节点恢复完毕。
Ceph的OSD往往采用三副本技术进行数据冗余,本实验平台在原生Ceph中添加HLRC OSD和其他对比纠删码OSD,以便更方便快捷地得到准确实验数据。
3.2 容错能力
容错能力是指纠删码能够纠正的错误数量,在分布式存储系统中代表其可以纠正的最大丢失节点数。纠删码的容错能力是存储系统非常重要的一项参数。图9主要展示了RGRC(24,11)、HLRC(13,7,2,1,1)、HLRC(13,5,3,2,1)和HLRC(13,5,3,3,1)四种不同编码方案的多节点容错能力。其横坐标表示当前丢失的节点个数,纵坐标表示当前丢失节点数情况下的修复概率。
对于四个不同参数的HLRC其各自的额外存储空间分别为11、11、11、13。同时对比HLRC(13,7,2,1,1)、HLRC(13,5,3,2,1)可以看出,在相同开销的情况下不同的参数以及不同的编码布局其修复效率也会不同。虽然两个编码方案都使用了11个额外存储空间,但是编码阵列有所不同,后者编码布局更为接近正方形,拥有更加优秀的修复效率,所以HLRC能够提供更为灵活的编码方式,可以满足更多的差异化需求。HLRC(13,5,3,3,1)可以通过增加少量冗余节点的方式达到相比之下最优秀的修复效率。但总体来看,不同HLRC的多节点容错能力都非常优秀,都能达到95%以上的修复率。
3.3 单节点修复开销
当存活节点越多时,系统出现节点故障发生数据丢失的概率最高,所以單节点出错是存储系统中面临的最为常见的错误。单节点修复性能就能很大程度地决定分布式存储系统的总体稳定性和可靠性,也是对于纠删码方案而言最为关键的性能指标之一。本节对RS(24,12)、Pyramid(24,12)、LRC(12,6,6)、DLRC(12,6,3,6)以及HLRC(12,7,2,2,1)(图中用H1标注)、HLRC(12,5,3,2,1)(图中用H2标注)、RGRC(24,12)进行了单节点平均修复开销的比较,结果如图10所示。
在相同的存储开销下,HLRC两个不同参数的编码方案提供了最优秀的平均单节点修复开销。其中HLRC(12,7,2,2,1)平均每一个单节点修复仅仅只需要额外的2.7个辅助节点即可完成;HLRC(12,5,3,2,1)也只需要3.458个辅助节点,相较于其他编码方案都有一定的优势。
在存储系统中,本节使用RS(24,12)、Pyramid(24,12)、
LRC(12,6,6)、DLRC(12,6,3,6)、HLRC(12,7,2,2,1)(图中用H1标注)、HLRC(12,5,3,2,1)(图中用H2标注)、RGRC(24,12)七种不同的编码方案分别对七个大小不同的文件进行编码,文件的大小对应为图11中的横坐标。最后统计出七种不同的编码方案中每一次的单节点修复开销,具体的实验结果如图11所示。
由图11可以看出,使用HLRC进行编码的两种方案对各个大小的文件都拥有较低的单节点修复开销,对比LRC、DLRC和Pyramid码都拥有更加优秀的单节点修复性能。其中HLRC(12,7,2,2,1)相较于RGRC的修复开销降低了11.66%,相较于Pyramid码的修复开销降低了39.23%,相较于LRC的修复开销降低了40%,相较于DLRC降低了48.56%,相较于RS降低了77.5%。
3.4 多节点修复开销
分布式存储系统中,多节点出错的可能虽然远小于单节点出错的可能,但依然是系统不稳定的因素之一。HLRC使用效率最优多节点修复算法来实现对多节点出错的恢复,使其在多節点恢复效率上依然拥有不错的能力,能够保证系统的可靠性。本节对Pyramid(24,12)、LRC(12,6,6)、DLRC(12,6,3,6)、
RGRC(24,12)以及HLRC(12,7,2,2,1)进行了部署和对比,具体结果如图12所示。
由图12可以看出,HLRC拥有较为优秀的多节点修复能力,在丢失节点数较少时,修复开销相较于其他方案更加优秀。在丢失3节点时,HLRC的多节点修复开销相较于RGRC、Pyra-mid码、DLRC和LRC分别减少了15.07%、18.9%、25.1%和22.4%。在丢失4节点时,HLRC的多节点修复开销相较于RGRC、Pyramid码、DLRC和LRC分别减少了5.90%、11.7%、16.9%和15.1%。即使在丢失5个节点时相较于三个其他编码方案也平均提升了6.61%。
在实际的测试环境中,本节使用RGRC(24,12)、(24,12)Pyramid、LRC(12,6,6)、DLRC(12,6,3,6)、HLRC(12,7,2,2,1)五种编码方案:分别对四个大小不同的文件进行了编码。最后统计在五种不同的编码方案中每一次的4节点平均修复开销,具体的实验结果如图13所示。
由图13可以看出,在实际的分布式环境之下,HLRC在不同的文件大小下,都拥有优秀的多节点修复开销。同时随着编码文件的变大,修复开销优势更大。
3.5 存储效率
存储效率是纠删码方案中较为关键的指标之一,其决定了编码方案实际存储的数据占用空间占总使用空间的比例,其比例越大,代表存储效率越高。图14反映了HLRC(14,5,3,1,1)、RGRC(12,7)、(12,10)Pyramid、LRC(16,8,2)、DLRC(14,2,4,8)以及RS(14,10)六种不同编码方案的存储效率。
根据图14可以看出,HLRC相较于RS和LRC牺牲了少许的存储效率,其中与LRC的存储效率相差约3.2%,但HLRC提供了更加优秀的节点修复性能和更低的节点修复开销。所以这些少许额外开销是可忽略不计的。相较于Pyramid码和DLRC、HLRC、RGRC拥有相近的容错能力,更加优秀的单节点修复性能,同时还相较于Pyramid码提高了3.79%的存储效率。总体来看,HLRC的存储效率处在可接受的范围内。
3.6 实验数据分析
HLRC的优势主要集中在单节点修复成本上,在少量节点丢失时修复成本依然优秀。在单节点修复开销上,HLRC相较于Pyramid码的修复开销降低了39.23%,相较于LRC的修复开销降低了40%,相较于DLRC降低了48.56%,相较于RS降低了77.5%,都拥有相当大的优势。同时在多节点修复开销上也有一定的优势,根据实验数据表明,HLRC在少量节点时丢失拥有较好的修复开销,随着丢失节点的增多,修复开销优势随之降低。这一特性和分布式存储系统的故障规律非常契合,所以其应用在分布式存储系统中用于降低修复开销具有一定的优势。
4 结束语
根据研究表明存储系统中约90%的数据丢失是单节点丢失[13],。本文提出的针对少量节点丢失进行优化的层次编码方案HLRC可以更好地保证分布式存储系统中数据的可靠性。HLRC拥有灵活的编码方式,在保证容错能力和存储效率的同时,提供更加高效低开销的少数节点出错修复能力。HLRC能够通过调整编码参数来改变编码时的布局,从而能够让HLRC在相同的存储开销情况下拥有不同的容错能力和修复开销,这样便能更好地适应分布式存储系统中不同的存储需求。但如何权衡编码参数来自适应地让分布式存储系统中容错能力和修复开销达到理论上最平衡的状态,还需后续的进一步研究。
参考文献:
[1]Shvachko K,Kuang H,Radia S,et al. The Hadoop distributed file system [C]// Proc of the 26th Symposium on Mass Storage Systems and Technologies. Piscataway,NJ: IEEE Press,2010: 1-10.
[2]Weil S A,Brandt S A,Miller E L,et al. Ceph: a scalable,high-performance distributed file system [C]// Proc of the 7th Symposium on Operating Systems Design and Implementation. Berkeley,CA: USENIX Association,2006: 307-320.
[3]Ghemawat S,Gobioff H,Leung S T. The Google file system [J]. ACM SIGOPS Operating Systems Review,2003,37(5):29-43.
[4]王意洁,许方亮,裴晓强. 分布式存储中的纠删码容错技术研究 [J]. 计算机学报,2017,40(1):236-255. (Wang Yijie,Xu Fang-liang,Pei Xiaoqiang. Research on erasure code-based fault-tolerant technology for distributed storage [J]. Chinese Journal of Computers, 2017,40(1): 236-255.)
[5]罗象宏,舒继武. 存储系统中的纠删码研究综述 [J]. 计算机研究与发展,2012,49(1): 1-11. (Luo Xianghong,Shu Jiwu. Summary of research for erasure code in storage system [J]. Journal of Computer Research and Development,2012,49(1): 1-11.)
[6]唐聃,蔡紅亮,耿微. RS类纠删码的译码方法 [J]. 计算机研究与发展,2022,59(3): 582-596. (Tang Dan,Cai Hongliang,Geng Wei. Decoding method of Reed-Solomon erasure codes [J]. Journal of Computer Research and Development,2022,59(3): 582-596.)
[7]杨松霖,张广艳. 纠删码存储系统中数据修复方法综述 [J]. 计算机科学与探索,2017,11(10): 1531-1544. (Yang Songlin,Zhang Guangyan. Review of data recovery in storage systems based on erasure codes [J]. Journal of Frontiers of Computer Science & Technology,2017,11(10): 1531-1544.)
[8]Blaum M,Brady J,Bruck J,et al. EVENODD: an efficient scheme for tolerating double disk failures in RAID architectures [J]. IEEE Trans on Computers,1995,44(2): 192-202.
[9]洪铁原,唐聃,熊攀,等. 存储系统中的局部修复阵列码模型 [J]. 计算机应用研究,2024,41(1): 193-199. (Hong Tieyuan,Tang Dan,Xiong Pan,et al. Local repairable array code model in storage systems [J]. Application Research of Computers,2024,41(1): 193-199.)
[10]Bhuvaneshwari P V,Tharini C. Review on LDPC codes for big data storage [J]. Wireless Personal Communications,2021,117(3): 1601-1625.
[11]Tu Yaofeng,Xiao Rong,Han Yinjun,et al. DDUC: an erasure-coded system with decoupled data updating and coding [J]. Frontiers of Information Technology & Electronic Engineering,2023,24(5): 716-731.
[12]Zhang Xingjun,Liang Ningjin,Liu Yunfei,et al. SA-RSR: a read-optimal data recovery strategy for XOR-coded distributed storage systems [J]. Frontiers of Information Technology & Electronic Engineering,2022,23(6): 858-876.
[13]Hafner J L. WEAVER codes: highly fault tolerant erasure codes for storage systems [C]// Proc of the 4th USENIX Conference on File and Storage Technologies. Berkeley,CA: USENIX Association,2005: 211-224.
[14]Huang Cheng,Simitci H,Xu Yikang,et al. Erasure coding in windows azure storage [C]// Proc of USENIX Annual Technical Conference. Berkeley,CA: USENIX Association,2012: 15-26.
[15]Huang Cheng,Chen Minghua,Li Jin. Pyramid codes: flexible schemes to trade space for access efficiency in reliable data storage systems [J]. ACM Trans on Storage,2013,9(1): article No 3.
[16]Meng Yulong,Zhang Lingling,Xu Dong,et al. A dynamic erasure code based on block code [C]// Proc of International Conference on Embedded Wireless Systems and Networks. [S.l.]: Junction Publishing,2019: 379-383.
[17]Wang Zihao,Xie Zheng,Tang Dan. An erasure code with low recovery-overhead based on a particular three-hierarchical redundancy structure [J]. International Journal of Network Security,2022,24(5): 965-974.
[18]Miyamae T,Nakao T,Shiozawa K. Erasure code with shingled local parity groups for efficient recovery from multiple disk failures [C]// Proc of the 10th USENIX Conference on Hot Topics in System Dependability. Berkeley,CA: USENIX Association,2014:.
[19]林軒,王意洁,裴晓强,等. GRC: 一种适用于多节点失效的高容错低修复成本纠删码 [J]. 计算机研究与发展,2014,51(S2): 172-181. (Lin Xuan,Wang Yijie,Pei Xiaoqiang,et al. GRC: a high fault-tolerance and low recovery-overhead erasure code for multiple losses [J]. Journal of Computer Research and Development,2014,51 (S2): 172-181.)
[20]张航,刘善政,唐聃,等. 分布式存储系统中的低修复成本纠删码 [J]. 计算机应用,2020,40(10): 2942-2950. (Zhang Hang,Liu Shanzheng,Tang Dan,et al. Erasure code with low recovery-overhead in distributed storage systems [J]. Journal of Computer Applications,2020,40(10): 2942-2950.)

