基于码重分布与汉明距离的线性码盲识别方法
李歆昊,张 旻
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
为了实现通信的可靠性,并提高通信的效率,信道编码在数字通信中得到了普遍的应用。信道编码识别分析不仅在智能通信领域有应用前景,尤其是在通信侦察或网络对抗领域有迫切的军事需求[1]。因此,信道编码的盲识别就成了现在面临的主要问题。
目前,信道编码盲识别分析技术方面的研究大部分都集中在卷积码的盲识别,对于线性分组码以及属于线性分组码的循环码和BCH码识别一般需要有一定的先验知识或在一定条件下进行。如文献[2]提出了二进制BCH码的一种识别方法,其基本思路是根据循环特性等得到备选多项式;再根据校正子权重和最小原则得到最优多项式;最后通过因式分解得到生成多项式的最终估计表达式。但此算法需要在帧长度已知的前提下进行,对于码字的全盲识别还不可行。文献[3]对低码率的二进制线性分组码采用码重分布距离对接收码字进行盲识别。但此算法需要知道码字起点。文献[4]针对BCH码的盲识别问题,提出了基于欧几里德算法的最大公因式的识别方法,主要是通过求取最大公因式确定码长,再由系数矩阵求出生成多项式。但在容错性方面,此算法具有抗末端误码能力,对前段和中段误码却无能为力。文献[5]利用码根信息差熵函数识别BCH码的码长,进而利用码根统计获取生成多项式的整数根,通过遍历该域中的本原多项式以寻求满足BCH码生成多项式根性质的码根和本原多项式,从而实现BCH码的盲识别。文献[6]则提出了BCH码的一种生成多项式快速识别方法,在采用已有的码根信息差熵的思想获得二进制本原BCH码分组长度之后,利用有限域同构的原理来求取生成多项式。但文献[5]和文献[6]都只对低码率的码字有较好的识别效果。文献[7]主要是利用线性分组码对偶码字的统计特性和 Walsh-Hadamard变换解线性方程组,并采用“3倍标准差”准则给出判决门限,通过判断对偶空间归一化维数的最大值来实现码长和码字起点的估计。该算法虽然可以完成对码长和码字起点的判别,但运算时间较长,需要多次迭代,导致计算量较大。可以看出,现有的识别技术离工程应用还有一定的距离,如何在全盲的情况下对线性码进行识别的问题还有待解决。
目前,针对线性分组码的识别方法,大多要在一定的先验知识下才能进行。如已知码字起点来识别码长,无法实现码字的全盲识别。因此,本文提出了一种利用码重分布和汉明距离相结合的方法,在无先验知识的情况下,识别码长和码字起点,进而得到生成矩阵或生成多项式,实现线性分组码的全盲识别。
1 线性分组码识别基础
1.1 线性分组码基础
定义1 将每k个信息位分为一组进行独立处理,变成长度为n(n>k)位的编码称为(n,k)分组码,其码率r=k/n,校验位长(n-k)。若校验位是信息位的线性组合,则称该编码为(n,k)线性分组码[7]。
1.2 盲识别的数学模型
对于线性分组码的盲识别问题,就是在不知道编码先验信息的情况下,通过对码字序列的分析处理,从而估计出其生成矩阵。其数学模型描述为:

式中,M={M1,M2,…,Mi,…}表示以k比特为分组单位的输入,Mi={M1,M2,…,Mk}表示第i时刻输入的k 个比特信息;C={C1,C2,…,Ci,…}表示以n比特为分组单位的编码输出序列,Ci={C1,C2,…,Cn}表示第i时刻输出的n个比特信息;G表示生成矩阵。实际中,C是通过对接收或侦察信号解调处理得到。因此,线性分组码的盲识别问题就是在仅知道C的前提下如何获得生成矩阵G,进而完成对信息的还原。
线性分组码识别分析包括的未知参数有:码字起点、码长和生成矩阵。对于截获到或侦察到的一串经过线性分组码编码的码字,我们要从中提取出有用的信息,必须对码字的编码形式和编码参数进行识别。由于截获数据的任意性,我们首先要对接收到的第一个码字的码字起点i(0≤i≤n)进行判断,本文称i为码组的码字起点,简称码字起点。
对于一串长度为L的数据流,假设它是(n,k)线性分组码,在确定了码字起点i之后,我们就从第i个码符号开始,对余下的L-i+1个码符号进行分组,每组长度为n,一共可以得到N=(L-i+1)/n」个码字(·」表示向下取整)。每一个码字为一行,组成一个N×n的矩阵,通过求解出的i和n可以得到生成矩阵G,从而解出信息序列。因此,求解码字序列的码长n和码字起点i成为了线性分组码盲识别的关键。
1.3 码重的理论分析
一个码字(或任何向量)的Hamming重量等于该码字中的非零元素的个数。对(n,k)线性分组码,定义码字C的码重分布W(C)为n+1个整数的集合W(C)={Ni=d,0≤d≤n},W (C)表示C 中Hamming重量为d的所有码组的数目。重量为d的码组在C中出现的概率pi就是该重量码组的码重分布概率。
定理1 对于一个数字通信系统,在一个码组中同时发生t个错误的概率为P(t),则
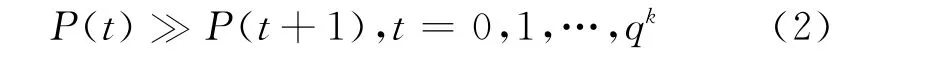
定理2 (n,k)线性分组码的k位信息生成的n位码字集v是n维空间V的子集,且v在V中的分布是非等概率的。
由定理1可知,误码对码组的码重分布影响很小,所以可根据码重分布来对码长进行估计。
对于(n,k)线性分组码,生成的码字集大小为2k≪2n,k位信息生成的n位码字的集合必定隶属于n位码字组成的码字集合,前者在后者中的分布是非等概率的。
如若估计码长不为真实码长,则分组内码字之间不存在约束关系,可认为0或1是等概率出现的,可假设此时数据的码重分布是等概率分布模型,不同码重的码组出现概率为:
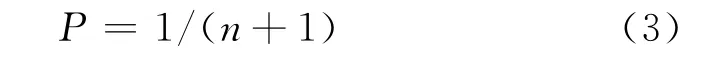
如设Pi为实际上重量为i的码组所出现的概率,定义码重分布距离公式为:
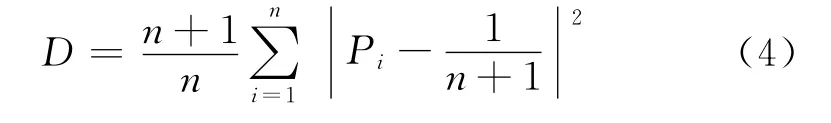
其中,n为估计码长,D为实际分布与均匀分布的方差距离。由上述定理可知,当码重分布距离D最大时的n 即为真实码长的估计^n[1]。
文献[3]在已知二进制线性分组码码字起点时,采用码重分布距离对接收码字进行识别。然而,在未知码字起点的全盲情况下,难以准确获得码长。
2 基于码重分布与汉明距离的盲识别方法
根据上述的理论基础,本文识别算法的步骤是:首先,根据码重分布,判断出码长,并粗判断出码字起点;然后,在粗判断出的码字起点上,利用汉明距离的方法,实现对码字起点的准确判断;最后,由识别出的码长和码字起点得到码字的生成矩阵。具体过程如下。
2.1 码重的码长判断
在全盲情况下,可以对二进制线性码进行遍历识别。当遍历到的码长准确时,会出现周期性的峰值,下面对此进行分析。
对于接收到的一串长度为L,码长为n的二进制线性分组码编码序列,当码字起点与真实码字起点相差太多或者码长与真实码长不一致时,码重分布类似随机,因而很难出现周期性的峰值。当码字起点与真实码字起点相差不多并且在码长判断准确的情况下,此时,码字起点判断错误对每组码字码重的影响要么没有,要么很小,所以对整体码重分布的影响可以忽略不计,码重分布还会出现周期性的峰值。峰值处对应的码长即为真实码长,而码字起点判断的正确与否则不能断定,不过必定小于真实值,所以可先进行码字起点的粗判断。假设通过遍历判断码长为n的情况,可以得到如式(5)所示的编码序列。
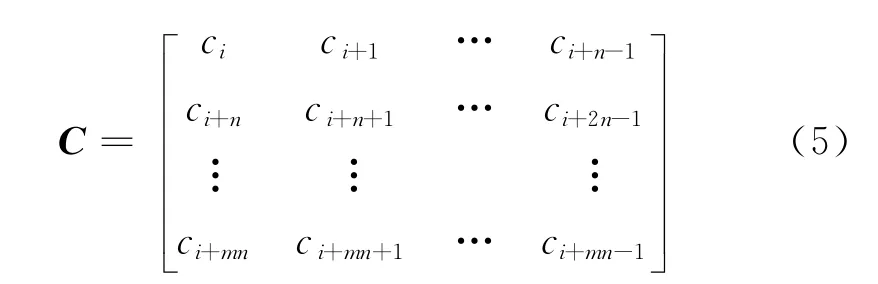
式(5)中,i为判断的码字起点,n是码长。当码字起点i与码字序列一致时,码重便取得固定的几个值,此时码重分布距离在码长n处所对应的D取得极大值。当码字起点i与码字序列存在偏差时,会导致码重取值的增多,造成码重分布分散,特别是在i值与码字序列起点相差越多时,造成码重分布越分散且极值越不明显。我们以(15,5)码字为例,做了码重分布取得极值与码字起点关系图1。

图1 码重分布距离与码字起点关系图Fig.1 Weight distribution distance codeword starting point diagram
从图1可以看出,当Ci与码字起点一致,即横坐标取值在1点时,码重分布取最大值;当相差7位,取在第8位时,即图1中横坐标取在8处,此时码重分布取得最小值。图2所示的就是i与码字起点相差3位到1位时的极值取值情况。
因此,可以利用码重遍历的方法,在码重分布出现周期性峰值时准确判断出码长。然而,遍历的方法还无法精确判断出码字起点,因为在实际情况中,存在误差且受编码序列随机分布的影响,加上相差位数较多时,造成了极值相差很小。所以,利用码重只能实现码字起点的粗判断。
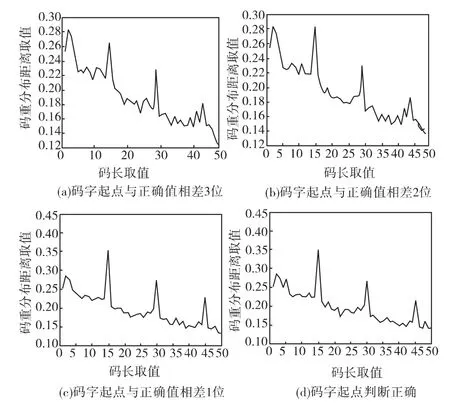
图2 码字起点取不同值时的码重分布情况Fig.2 Codeword starting point for different values of code weight distribution
2.2 汉明距离的码字起点精确识别
设xi和yi是由码符号集{0,1}中的码符号“0”和“1”组成的长度为n的两个符号序列
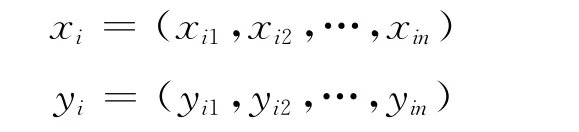
其中xi1,xi2,…,xin∈ {0,1};yi1,yi2,…,yin∈ {0,1}。xi和yi之间相同时刻的不同码符号的位置数dH(xi,yi)称为xi和yi之间的汉明距离。
最小汉明距离d0是(n,k)分组码的一个重要参数,它表明了分组码抗干扰能力的大小,纠错码的基本任务之一就是构造出码率R一定,d0尽可能大的码。线性分组码码字之间的汉明距离一定大于等于该分组码的最小距离和非零码字的最小重量。
在纠错编码领域里,设计最差的分组码的性能是只检测和纠正1个随机错误,即e=1。对于任意(n,k)分组码,若要在码字内:1)检测e个随机错误,则要求码的最小距离d0≥e+1;2)纠正t个随机错误,则要求d0≥2t+1[8]。因此分组码的最小距离d0≥3。分组码要有检测和纠正的作用,最小距离d0一定不等于1。
对于上述已经精确判断出码长n和粗判断出码字起点i的码字序列,从码字起点i开始,按照码长n对序列进行划分,并画出划分后码字之间的汉明距离分布图。判断在汉明距离为1和2的位置处是否有分布,若有分布,则码字起点向后移一位,继续判断,直到汉明距离为1和2处没有分布为止。此时的码字起点i即为正确的码字起点。
2.3 识别生成矩阵
对于一个二元域GF(2)上的(n,k)线性分组码,可以由k个线性独立的码字组成的基底张成。把这k个线性独立的码字按行排列,即可得到(n,k)线性分组码的生成矩阵G。因此,对于一组编码后的码字,要想得到它的生成矩阵G,只要从中找出k个线性独立的码字即可。
在码字起点和码长已知的情况下,就可以用码长对接收序列进行划分,选取一定数目的码字建立待化简矩阵G′,通过对G′进行二进制运算的化简,求出矩阵的k个最大线性无关向量,即得到生成矩阵G[8]。
为了避免误码情况对结果的影响,可以进行多次化简计算,选取出现概率最高的一组最大线性无关向量组作为生成矩阵,从而完成对生成矩阵的识别[8]。
3 仿真实验
3.1 实验一 编码参数的识别
为了说明本文算法的有效性,使用matlab软件,随机产生码长为n的码字序列进行编码识别。各选取1 160组码字,对(7,4)、(15,5)和(31,16)三组典型的二进制线性分组码进行识别:
1)基于码重分布的码长判断
如图3所示的是(7,4)、(15,5)和(31,16)三种典型的二进制线性分组码的码重分布情况。可以发现,在三组图片中,当码长n识别正确时,码长n及码长整数倍an(a∈N)处所对应的码重分布取到峰值。因为,此时的码长为真实码长,分组内码字之间存在约束关系,所以各码重的出现不存在随机性,此时的方差距离D取到极大值,因此可以将其判断为真实码长。
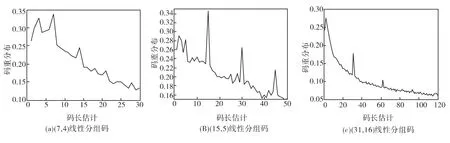
图3 三种不同的二进制线性分组码的码重分布情况Fig.3 Three different binary linear block code's code weight distribution
2)基于汉明距离的码字起点判断
如图4所示的是(7,4)、(15,5)和(31,16)三种典型的二进制线性分组码的汉明距离分布情况。在无误码的情况下,当码字起点判断正确时,各个码组内存在线性约束关系,且这三种码字都有检错纠错能力,因此,最小汉明距离d0≥3。所以,在d0=1和d0=2的位置处,汉明距离的分布应该等于零。由图4也可以看出,虽然三种码字的纠错能力不同,导致汉明距离的分布情况不同,但总体趋势还是一致的,即汉明距离分布的取值主要集中在某几点处,且在低值处的分布都为零。若码字起点判断错误,此时的编码不具有检错与纠错的能力,汉明距离的分布在各个取值处也就相对平均。因此,运用汉明距离的分布可以正确地判断出码字起点。

图4 三种不同的二进制线性分组码的汉明距离分布情况Fig.4 Three different binary linear block code's Hamming distance distribution
3)生成矩阵的获取
对于线性分组码,在知道了码长和码字起点以后,就能很容易地求得生成矩阵。在起点处,以码长划分线性分组码序列,选取一定数量互不相同的码字组成待化简矩阵G′,对矩阵进行基于二进制运算的化简,最终得到以上三组序列的生成矩阵为:

3.2 实验二 误码的影响
在上述的实验条件下,本文加入了误码,并仿真了在误码率不断升高的情况下对识别效果的影响。
图5所示的是(7,4)线性分组码、(15,5)线性分组码和(31,16)线性分组码在误码率不断升高的情况下,能够成功识别的概率图。可以看出,在误码率小于1%的情况下,(7,4)线性分组码和(31,16)线性分组码成功识别的比例在90%左右,而(15,5)线性分组码成功识别的概率可以达到100%。随着误码率的升高,(15,5)线性分组码的抗噪性能要好得多,而(7,4)线性分组码和(31,16)线性分组码在误码率接近2%的时候,识别的成功率也在50%左右,所以该方法具有较好的容错性能和较高的实际应用价值。
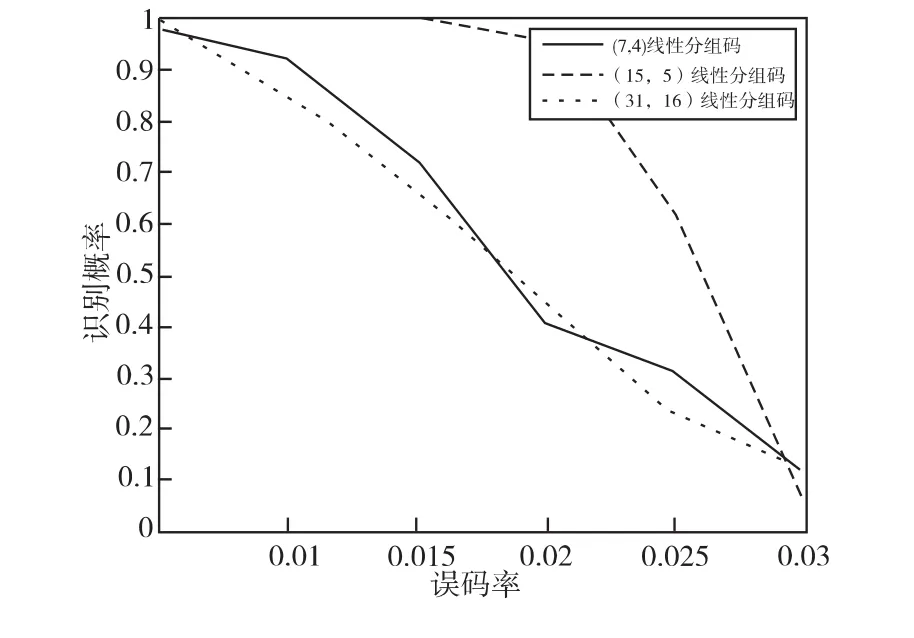
图5 存在误码下的识别概率Fig.5 Presence of the bit error probability of identification
4 结论
本文提出了基于码重分布与汉明距离的线性分组码盲识别方法。该方法利用码组内码重分布不等概的性质,通过观察码重分布的极值取值情况,来判断出正确的码长并初步判断出码字起点;接着,从已判断出的码字起点开始,利用纠错码的纠错能力与汉明距离之间关系的性质,利用汉明距离的分布,准确判断出码字起点,进而完成对线性分组码的盲识别。仿真实验表明,在误码率一定的情况下,以上的方法仍可以很好地识别出低码率的二进制线性分组码。但随着识别码字码长的增加,计算量会不断增大,导致运算时间变长,所以算法还有待改进优化。
[1]张永光,楼才义.信道编码及其识别分析[M].北京:电子工业出版社,2010.
[2]王甲峰,岳旸,权友波.二进制BCH码的一种盲识别方法[J].信息与电子工程,2011,9(5):591-595.WANG Jiafeng,YUE Yang,QUAN Youbo.Blind recognition method of binary BCH code[J].Information and Electronic Engineering,2011,9(5):591-595.
[3]昝俊军,李艳斌.低码率二进制线性分组码的盲识别[J].无线电工程,2009,39(1):19-22.ZAN Junjun,LI Yanbin.Blind recognition of low coderate binary linear block code [J].Radio Engineering.2009,39(1):19-22
[4]王兰勋,李丹芳,汪洋.二进制本原BCH码的参数盲识别[J].河北大学学报,2012,32(4):416-428.WANG Lanxun,LI Danfang,WANG Yang.Blind recognition of binary primitive BCH codes parameters[J].Journal of Hebei University,2012,32(4):416-428
[5]杨晓静,闻年成.基于码根信息差熵和码根统计的BCH码识别方法[J].探测与控制学报,2010,32(3):69-73.YANG Xiaojing,WEN Niancheng.Recognition method of BCH codes based on roots information dispersion entropy and roots statistic[J].Journal of Detection & Control,2010,32(3):69-73.
[6]吕喜在,黄芝平,苏绍璟.BCH码生成多项式快速识别方法[J].西安电子科技大学学报,2011,38(6):159-172.LV Xizai,HUANG Zhiping,SU Shaojing.Fast recognition method for generator polynomial of BCH codes[J].Journal of Xidian University.2011,38(6):159-172.
[7]杨晓炜,甘露.基于 Walsh-Hadamard变换的线性分组码参数盲估计算法[J].电子与信息学报,2012,34(7):1643-1646.YANG Xiaowei,GAN Lu.Blind estimation algorithm of the linear block codes parameters based on WHT[J].Journal of Electronics &Information Technology.2012,34(7):1643-1646.
[8]闫郁翰,汤建龙.基于汉明距离的二进制线性分组码盲识别方法[J].通信对抗,2011(4):20-23.YAN Yuhan,TANG Jianlong.Blind recognition method of binary linear block codes based on hamming distance[J].Communication Countermeasures,2011(4):20-23.

