空时分组码盲识别技术综述
闫文君,张立民,凌 青,孔东明
(1.海军航空工程学院电子信息工程系,山东 烟台 264001;2.海军航空工程学院融合所,山东 烟台 264001;3.海军装备部,山西 太原 030027)
0 引言
近年来,无线通信技术迅猛发展,对无线系统传输信息数量和传输速率的要求越来越高,一个突破传输信息数量增多、传输速率加快的重要技术就是多输入多输出系统(Multiple Input Multiple Output,MIMO)[1]。而解决多径传播中时变多径衰落问题的有效手段之一是天线分集技术[2]。利用天线分集的方法有2 种:接收分集和发射分集。
1)接收分集可以获得很大的性能增益,它不仅有较好的链路预算资源,而且具有更强的抗邻道干扰能力。来自不同接收天线的信号通常是通过数字硬件进行合并,其性能增益与分集效果相关,分集效果受不同天线不同路径的信号之间的衰落的相互独立性影响。目前很多通信系统的基站都是采用接收分集,例如全球移动通信系统(GSM)[2]的基站通常采用2 根接收天线。然而,由于接收端功率、天线尺寸和成本的限制,在接收端增加天线并非用户乐于接受的。
2)发射分集是在发射端增加发射天线,它可以改善整个无线通信系统的通信质量,而不需要每个接收者改善设备,这对于通信网络运营商负担不大,接收端用户也乐于接受。增加基站复杂度,减少接收端复杂度也是未来无线通信系统发展的要求[3]。
空时分组码(Space-Time Block Code,STBC)是随着分集技术的发展而出现的一种非常有效的信道编码方式[4]。空时分组码盲识别技术是一个新的重要的信号处理方向。如图1 所示,识别的问题主要有:发射天线数识别[5]、调制方式识别[6]、正交识别[7]和类型识别[8-22]4 个方面。其中,空时分组码类型识别分为基于最大似然的算法[8]和基于特征参数的算法。后者又分为基于相关函数的算法[9-14]和基于循环平稳的算法[15-22]。

图1 空时分组码识别问题分类
目前还没有针对空时分组码类型识别的综述性文献,笔者将针对这一问题进行讨论,介绍具有代表性的识别算法,对这些识别算法进行比较,并给出结论。
1 空时分组码盲识别技术发展概况
2007 年之前,对于空时分组码盲识别的研究大多建立在半盲条件下。2007 年,M.Shi 等提出识别STC(Space-Time Block)和BLAST(Bell Lasbs Layered Space-Time Architecture)的相关函数算法和循环平稳算法[5],这2 种算法后来发展成为2 种主要的识别算法;2008 年,M.R.DeYoung 等首次提出基于四阶循环累积量的空时分组码识别算法,利用循环累积量的循环频率的特性,对SM(Spatial Multiplexing)和Alamouti STBC[4]进行了识别;2008 年到2011 年,V.Choqueuse 和G.Burel 的团队对空时分组码盲识别进行了研究。2008 年,V.Choqueuse 等基于二阶统计特性,提出利用空时分组码冗余性和相关性算法,该算法容易实现,但该算法在全盲条件下,仅对部分码率较小的STBC 识别效果较好[9-10]。2010 年,该团队提出基于最大似然的识别算法[8],最大似然的算法能够得到最优的识别性能,但识别之前需要进行信道估计,并需要调制信息和噪声信息,识别计算复杂度较高。鉴于基于二阶统计特性和基于最大似然识别算法的缺点,2011 年,V.Choqueuse 提出基于高阶统计特性的识别算法[16],该算法不需要对信道进行估计,对码率较大的码识别性能较好,但识别性能上尚有待改进;2012 年,O.A.Dobre 的团队在空时分组码的识别中作出重要贡献。2012 年,M.Marey 和O.A.Dobre 提出基于四阶循环平稳的空时分组码识别算法[18],在识别中对不同空时分组码的循环频率进行检测,并将基于四阶循环平稳的算法第一次应用到传输损耗的条件下[19]。至此,对空时分组码盲识别的研究仅限于多接收天线的条件下,对单接收天线上述算法并不完全适用。通过引言中的分析可知,单接收天线系统是客观存在的,研究单接收天线的空时分组码识别算法势在必行。随后,O.A.Dobre 等分别使用基于高阶累积量的算法[15,17]和K-S 检测的算法[14],对单接收天线下空时分组码盲识别进行了研究,取得了不错的进展,到目前为止,这3 篇文献是研究单接收天线下空时分组码识别算法的较好的参考资料。2014 以来,随着OFDM-STBC 系统的发展,O.A.Dobre 等开始对OFDM 条件下的空时分组码盲识别进行研究[11,14,20],与OFDM 结合的空时分组码识别与普通的识别有很大的不同,最基本的是空时分组码编码方式不一样,普通的空时分组码编码是对每一个符号进行空时编码,而OFDM 条件下是对符号向量进行编码,识别过程也不尽相同。目前该团队在OFDM 条件下的识别取得了一定的进展,但仅限于限制接收天线数的条件下,寻求一种适用于不限定天线数的识别算法是将来空时分组码识别发展的方向。
总之,空时分组码是一种新兴的编码形式,它在工程上的应用还较少,对于空时分组码盲识别领域的研究不多,随着空时分组码在实际中的应用,空时分组码盲识别技术定会取得广泛的发展和突破。
2 空时分组码
给定一个使用空时分组码的线性通信系统,其发射天线数为nt,接收天线数为nr,每个空时分组码矩阵传输符号数为ne,第k 个码矩阵传输的符号为Sk=[sk(1),…,sk(ne)],经历的时间间隔数为L,则空时分组码码矩阵可表示成nt×L 维向量,记为Cu(Sv),u和v 表示空时分组码的第v 个传输块的第u 列,其中0 <u ≤L。
空时分组码类型很多,常用的空时分组码有4种,大多数的识别算法是在这4 种空时分组码之间进行识别,分别为:
1)SM(Spatial Multiplexing,空间复用):发射天线数nt=1,码矩阵长度L=1[8],则有(严格地讲SM 并非空时分组码):
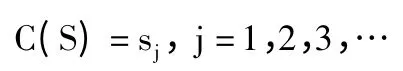
2)AL(Alamouti STBC):发射天线数nt=2,码矩阵长度L=2[4],则有:
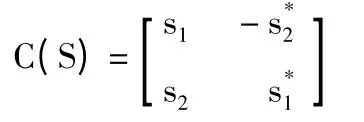
3)STBC3:发射天线数nt=3,码矩阵长度L=4[9],则有:
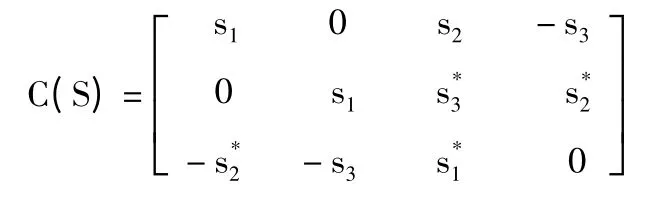
4)STBC4:发射天线数nt=3,码矩阵长度L=8[9],则有:

3 最大似然算法
空时分组码识别的基于最大似然(Maximum Likelihood,ML)的算法[8]是假定不同类型的接收信号在接收端是已知的,运用最大似然公式进行识别。在识别之前,除信号类型外,还需要已知传输信号的调制方式、相位、噪声、时延和信道参数。它的识别过程是通过构造多元假设检验来完成的。根据处理未知参数的方式不同,最大似然算法可分为3 类:平均似然比检验(Average Likelihood Ratio Tests,ALRT)、广义似然比检验(Generalized Likelihood Ratio Tests,GLRT)和混合似然比检验(Hybrid Likelihood Ratio Tests,HLRT)。如图2 所示。

图2 3 种空时分组码识别算法
1)ALRT 是使用随机变量模拟未知参数和数据,根据这些参数的平均值计算似然方程。因此,需要预先知道上述未知量的概率密度函数。一般的处理是认为未知参数独立同分布。对于与信号有关的参数,取通用的设置,比如对于相位偏移,取-π~π 之间的均匀分布。
2)GLRT 使用确定值模拟未知参数,在每次假设检验中,使用最大似然估计计算似然方程。很显然,ML 估计的结果很大程度上依赖假设检验的设定。未知参数的增多会增大算法的复杂度[22],同时算法的准确性很大程度上依赖于参数估计的准确性。
3)HLRT 同时使用随机数和确定值模拟未知参数。HLRT 的算法复杂度同样较高,与GLRT 类似,HLRT 算法的准确性依赖于参数估计的准确性[23]。
ML 算法能够提供使识别概率最大的最优解,因此在已知信道信息和噪声信息的条件下,ML 算法是识别效果最好的算法。但在信道信息、调制信息和噪声信息未知的情况下,ML 算法的性能则有待商榷[1,22]。
4 基于特征参数的算法
基于特征参数的算法(Features Based,FB)是通过将接收信号进行一系列变换,不同空时分组码信号之间的差异,以此作为特征参数对不同空时分组码进行识别。FB 算法最重要的问题是寻找恰当的特征参数。目前常用的FB 算法主要有:相关函数算法和高阶循环谱算法。
4.1 相关函数算法
基于相关函数的算法是通过计算接收信号的协方差矩阵或相关函数来获得特征参数,从而进行识别。相关函数的算法主要分为2 类:
1)非零法[9-13]。通过观察相关函数的值是否非零进行识别;
2)分布法[14]。根据构造的相关参数序列的分布特性进行识别。不同于最大似然算法,基于相关函数的算法不需要预先知道信道信息、调制信息和噪声信息。
在传输符号独立同分布的条件下,由空时分组码矩阵可以看出,传输符号在码矩阵内是相关的,而在码矩阵之间是独立同分布的。根据这一特性,实施相关函数算法。
4.1.1 非零法
非零法中相关函数的定义为[9]:

其中,r(k)为第k 个接收信号,τ 为时延参数。根据码矩阵元素的相关性,当τ <L 时,y(τ)≠0;当τ≥L时,y(τ)=0。由于不同STBC 传输经历的时延L 不同,可以设定不同的时延参数τ 对STBC 进行识别。
用更一般的表述方式,SM,AL,STBC3 和STBC4传输经历的时延L 分别为1,2,4,8。可以构造如图3所示的决策树,并得出如下结论:当τ≥8 时,4 种码的相关函数值均为0;当τ≥4 时,STBC4 的相关函数值为非0,其他3 种码为0;当τ≥2 时,STBC3 和STBC4 的相关函数值为非0,其他2 种码为0;当τ≥1时,SM 相关函数值为0,其他3 种为非0。
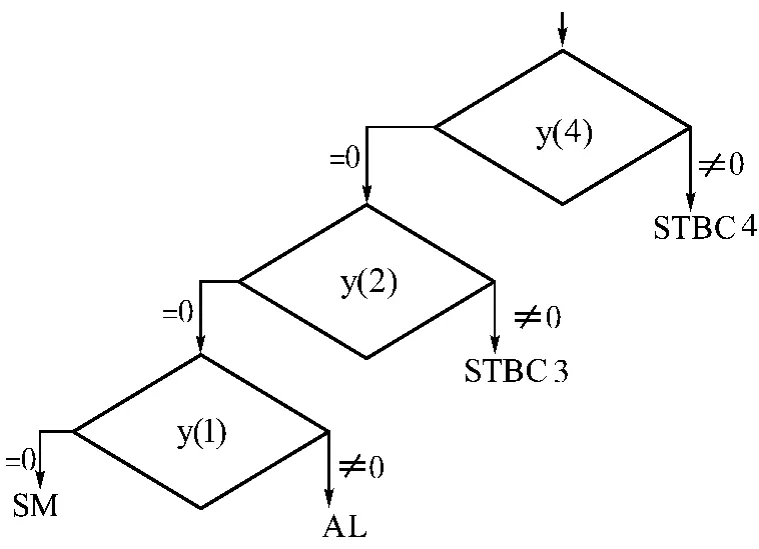
图3 非零法识别决策树
4.1.2 分布法
分布法[14]的思想是将接收信号分为相关函数分布不同的2 段,假设接收端接收信号序列为:
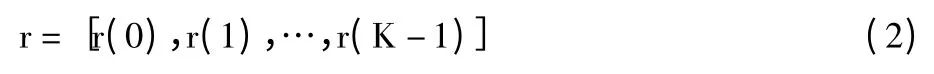
不失一般性,以SM 和AL 为例,当时延参数τ=1时(如图4 所示),将接收信号分为不重叠的2 段:
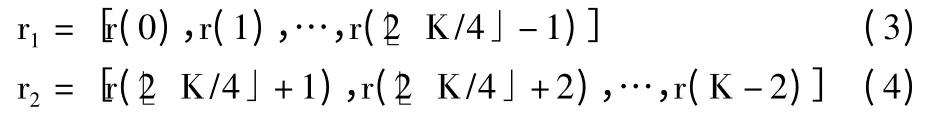
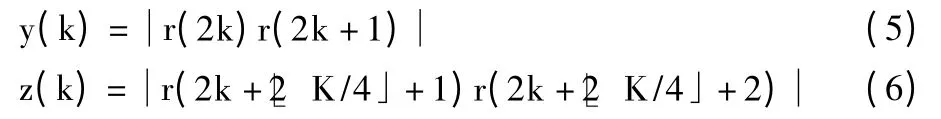
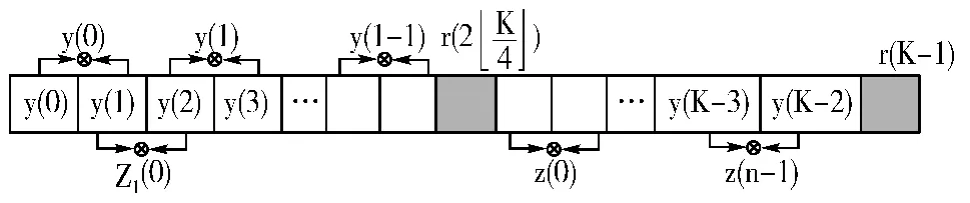
图4 分布法信号序列划分方法
同样,依据空时分组码码矩阵元素相关性不同,对于SM 信号,式(5)和式(6)均为独立同分布;对于AL 信号,式(5)和式(6)其中之一为独立同分布,而另一个并非独立同分布。通过检验是否同一分布的算法,则可以对SM 和AL 进行区分,如K-S 检测算法。
同理,当时延参数τ 不同时,不妨取1,2,4,同样可以区分STBC3 和STBC4。
4.2 高阶循环平稳算法
高阶循环平稳算法使用接收信号的二阶[19-21]或四阶循环平稳[15-18]作为计算特征参数的方法,其目的是寻找接收信号的四阶循环谱中是否有循环频率,部分文献也称之为基于高阶统计量的算法[15-17]。其中二阶或四阶循环平稳是由其二阶时变自相关函数的傅里叶变换构成。二阶时变自相关函数定义为[23]:

其中,t 为周期T0内时间点,τ 为时延参数。接收信号傅里叶系数为:
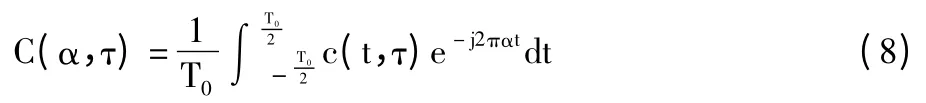
其中α 为时变自相关函数的循环频率。
四阶循环平稳的定义有2 种方式:由接收信号四阶矩的傅里叶变换来定义和由接收信号四阶累积量的傅里叶变换来定义。其中,在时延参数τ 下,四阶矩定义为[19]:

其中,k 为接收信号的序号。
由于不同STBC 码矩阵元素分布不同,对应的四阶矩的分布特性不同。取四阶矩的离散傅里叶变换作为特征参数,定义接收信号y 的离散傅里叶变换为:
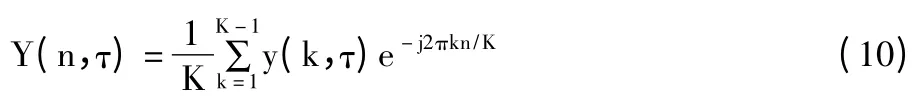
其中,K 为接收信号长度,n=0,1,…,K-1。
四阶累积量的傅里叶展开定义为[15]:
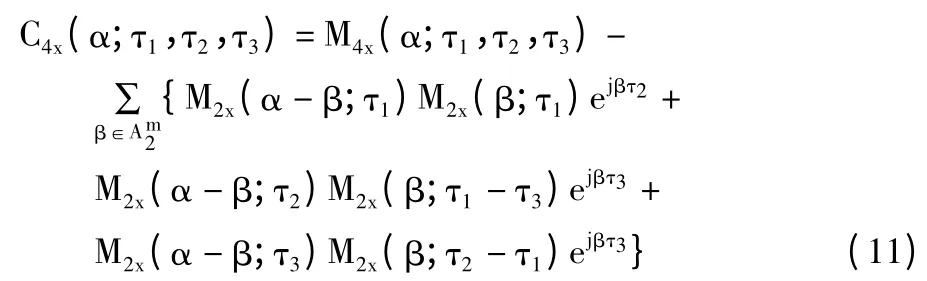
其中,Mkx为k 阶循环矩,其定义为:

以四阶矩定义的四阶循环平稳为例,当时延参数τ=4 时,4 种空时分组码接收信号的四阶循环平稳的曲线如图5 所示。可以看出STBC4 具有尖峰而其他3 种码没有。通过3 种方式可以识别STBC4[15]:
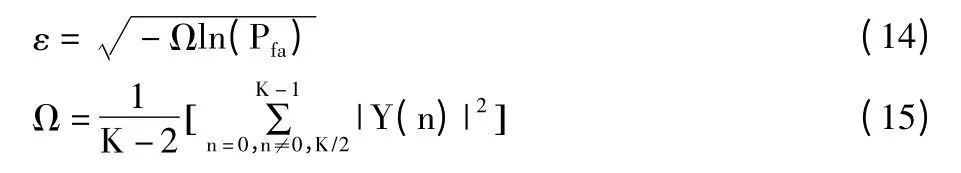
其中,K 为接收信号长度,Pfa为置信区间。
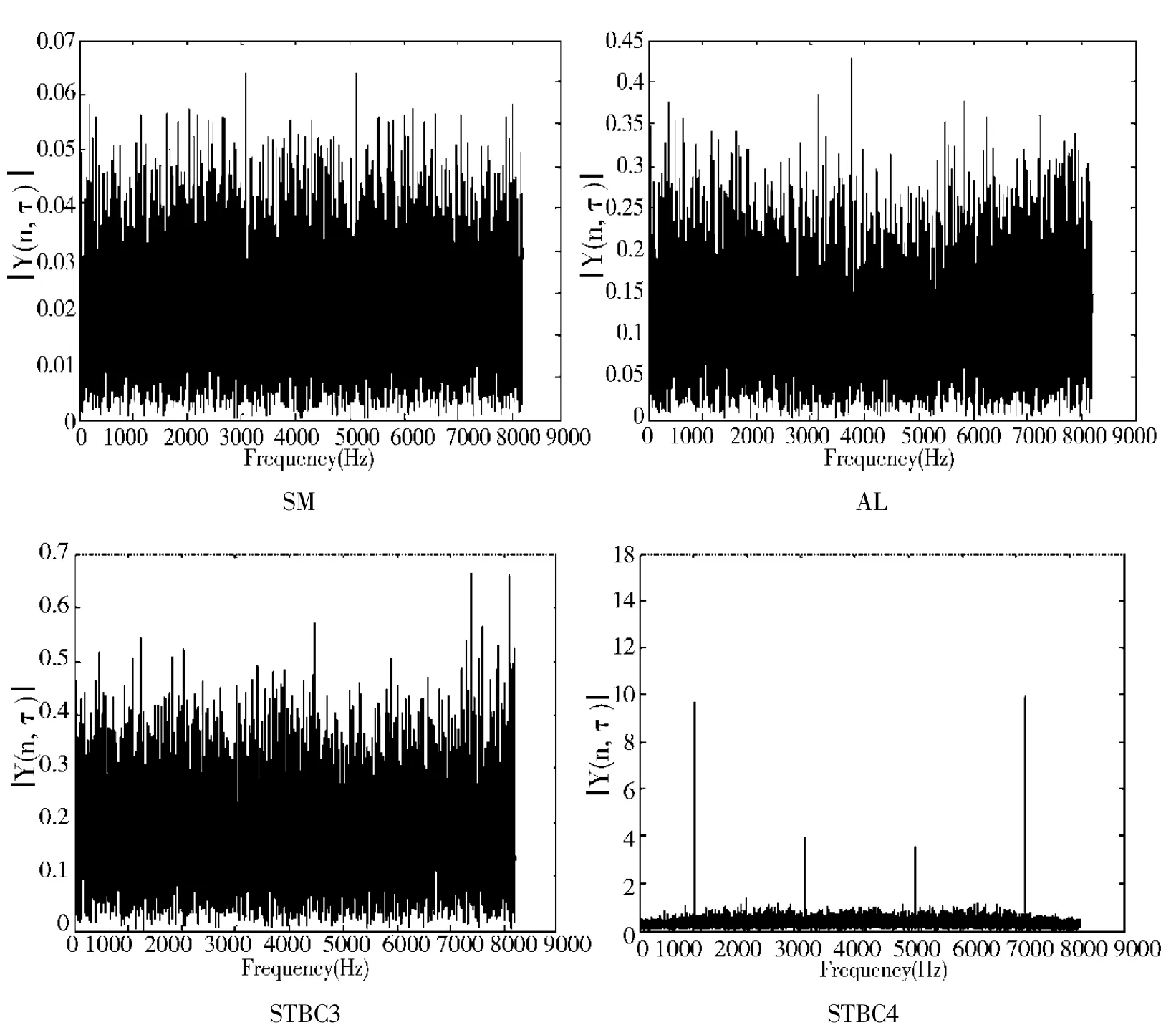
图5 信噪比SNR=10dB,时延参数τ=4 时,不同空时分组码分布图
5 算法性能分析和比较
本节对具有代表性的算法进行比较。算法的假设条件、计算复杂度等性能仅限于当前公开发表的研究,随着将来算法改进和新算法提出,下列算法的假设条件和计算复杂度等性能会发生变化。
3 种算法的性能比较如表1 所示。取4 篇具有代表性的文献进行比较,分别为:最大似然法[8]、非零法[9]、分布法[14]、循环平稳法(取第3 种识别方式)[15]。接收信号数为1024,调制方式为QPSK,信道和噪声分别采用瑞利信道和高斯噪声。单接收天线条件下,4 种算法性能如表1 所示;4 根接收天线条件下,4 种算法性能如表2 所示;4 种算法计算复杂度如表3 所示。
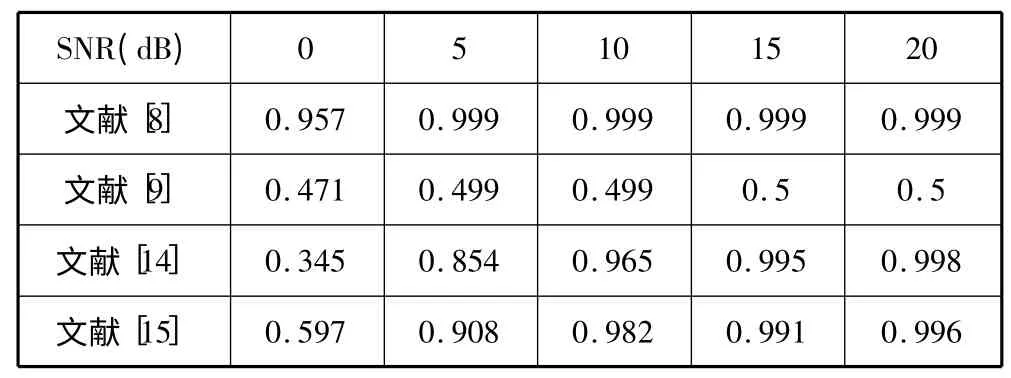
表1 4 种算法在单接收天线条件下性能比较
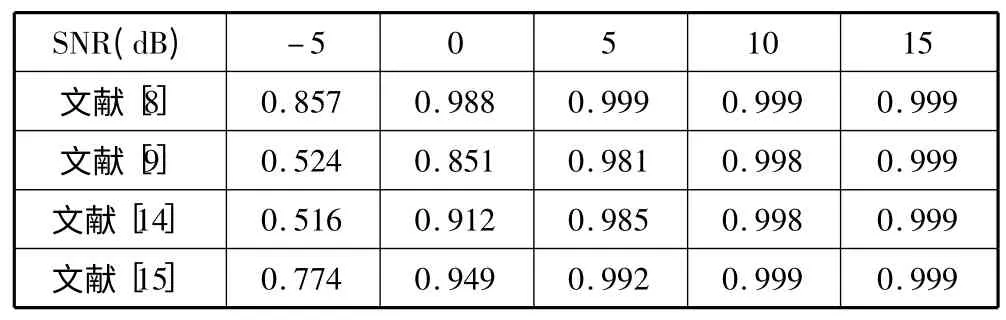
表2 4 种算法在4 根接收天线条件下性能比较

表3 4 种算法计算复杂度比较
1)基于最大似然的算法:识别性能最高,能适用于单接收天线情况和多接收天线情况,缺点在于计算复杂度高,识别之前需要预先估计信道信息、噪声信息和调制信息。
2)基于相关函数的算法:算法简单,识别所需接收信号采样数较少。其中,非零法仅适用于多接收天线的情况,分布法不仅适用于多接收天线的情况还适用于单接收天线的情况。非零法对于SM 和STBC4 区分较好,对AL 和STBC3 区分能力较弱。总体来讲,基于相关函数的算法性能(尤其是低信噪比下性能)不如基于最大似然的算法和基于循环平稳的算法。
3)基于循环平稳的算法性能介于基于最大似然算法和基于相关函数的算法之间。其中,基于二阶循环平稳的算法仅适用于多接收天线的情况,基于四阶循环平稳的算法不仅适用于多接收天线的情况还适用于单接收天线的情况。该算法能够解决传输损耗条件下空时分组码识别问题[20]。基于四阶循环平稳的算法由于需要利用接收信号的四阶统计特性进行识别,所需的样本数较大,计算复杂度较高,但在低信噪比下识别性能较好。
6 结束语
空时分组码的盲识别具有广泛的应用前景,其在全盲条件下的识别是一个新的重要方向,目前针对该领域的研究还较少,从空时分组码的提出到现在,空时分组码及其识别技术在理论和实现上取得了丰硕的成果,但同时应该看到,这个年轻的学科存在许多问题,特别是如下几点需要完善:
1)接收天线数较少,甚至只有一根接收天线下空时分组码盲识别问题。前文已经提到,减少接收端复杂度,增加基站的复杂度是当前一种有效的节约成本、增大传输数据数量和速率的方式,也是用户乐于接受的方案。单接收天线无线通信系统是客观存在的,因此单接收天线下和低信噪比下的空时分组码的盲识别应得到特别关注。
2)OFDM 与空时分组码相结合条件下的空时分组码盲识别。OFDM 是下一代无线通信标准,OFDM条件下空时分组码识别的算法还较少,且只停留在限定接收天线数的条件下,在任意接收天线数下的OFDM-STBC 识别问题还没有人研究。
3)STBC 信号的调制识别算法较少。STBC 条件下的信号有着与普通信号不同的特性,然而对应的调制识别算法还仅限于相移键控,还需要适用范围更广泛的调制识别算法。
笔者总结了当前空时分组码类型识别的2 大类方法:基于最大似然的算法和基于特征参数的算法。对基于最大似然的算法进行了分类,介绍了其识别的基本原理;对基于特征参数的2 类算法:基于相关函数和基于循环平稳的算法的关键技术和主要实施过程进行了描述。最后通过仿真对最大似然算法和基于特征参数的算法的优缺点进行了比较。目前空时分组码的应用还处于发展阶段,随着空时分组码应用的越来越广泛,它的盲识别技术也会向着更广、更深的方向发展。
[1]Dobre O A,Abdi A,Bar-Ness Y,et al.A survey of automatic modulation classification techniques:Classical approaches and new trends[J].IET Communications,2007,1(2):137-156.
[2]Larsson E G,Stoica P.Space-Time Block Coding for Wireless Communications[M].任品毅,译.西安:西安交通大学出版社,2006:1-4.
[3]Dobre O A.Signal identification for emerging intelligent radios:Classical problems and new challenges[J].IEEE Instrumentation & Measurement Magazine,2015,18(2):11-18.
[4]Alamouti S M.A simple transmit diversity technique for wireless communications[J].IEEE Journal on Selected Areas in Communications,1998,16(8):1451-1458.
[5]Shi Miao,Bar-Ness Y,Su Wei.Adaptive estimation of the number of transmit antennas[C]// IEEE Global Telecommunications Conference.2007:3034-3039.
[6]Marey M,Dobre O A.Blind modulation classification algorithm for single and multiple-antenna systems over frequency-selective channels[J].IEEE Signal Processing Letters,2014,21(9):1098-1102.
[7]赵知劲,谢少萍,王海泉.OSTBC 信号累积量的特征分析[J].电路与系统学报,2013,18(1):150-155.
[8]Choqueuse V,Marazin M,Collin L,et al.Blind recognition of linear space time block codes:A likelihood-based approach[J].IEEE Transactions on Signal Processing,2010,58(3):1290-1299.
[9]Choqueuse V,Yao K,Collin L.Hierarchical space-time block code recognition using correlation matrices[J].IEEE Transactions on Wireless Communications,2008,7(9):3526-3534.
[10]Choqueuse V,Yao K,Collin L,et al.Blind recognition of linear space time block codes[C]// Proc.IEEE International Conference Acoustics Speech and Signal Processing.2008:2833-2836.
[11]Marey M,Dobre O A,Liao B.Classification of STBC system over frequency-selective channels[J].IEEE Transactions on Vehicular Technology,2015,64(5):2159-2164.
[12]Qian Guobing,Li Liping,Luo Minggang,et al.Blind recognition of space-time block code in MISO system[J].EURASIP Journal on Wireless Communications and Networking,2013,2013(6):201-205.
[13]Luo Minggang,Gan Lu,Li Liping.Blind recognition of space-time block code using correlation matrices in a high dimensional feature space[J].Journal of Information &Computational Science,2012,9(6):1469-1476.
[14]Mohammadarimi M,Dobre O A.Blind identification of spatial multiplexing and Alamouti space-time block code via Kolmogorov-Smirnov (K-S)test[J].IEEE Communications Letters,2014,18(10):1711-1714.
[15]Eldemerdash Y A,Marey M,Dobre O A,et al.Fourth-order statistics for blind classification of spatial multiplexing and Alamouti space-time block code signals[J].IEEE Transaction on Communications,2013,61(6):2420-2431.
[16]Choqueuse V,Mans our A,Burel G,et al.Blind channel estimation for STBC system using higher-order statistics[J].IEEE Transactions Wireless Communications,2011,10(2):495-505.
[17]Eldemerdash Y A,Dobre O A,Marey M,et al.An efficient algorithm for space-time block code classification[C]// IEEE Global Communications Conference.2013:3329-3334.
[18]Deyoung M R,Health R,Evans B L.Using higher order cyclostationarity to identify space-time block codes[C]// IEEE Global Telecommunications Conference.2008:3370-3374.
[19]Marey M,Dobre O A,Inkol R.Cyclostationarity-based blind classification of STBCs for cognitive radio systems[C]// IEEE International Conference on Communications.2012:1715-1720.
[20]Marey M,Dobre O A,Inkol R.Classification of space time block codes based on second-order cyclostationarity with transmission impairments[J].IEEE Transaction on Wireless Communication,2012,11(7):2574-2584.
[21]Karami E,Dobre O A.Identification of SM-OFDM and AL-OFDM signals based on their second-order cyclostationarity[J].IEEE Transactions on Vehicular Technology,2015,64(3):942-953.
[22]Panagiotou P,Anastasoupoulos A,Polydoros A.Likelihood ratio tests for modulation classification[C]// The 21st Century Military Communications Conference Proceedings.2000:670-674.
[23]Hameed F,Dobre O A,Popescu D C.On the likelihoodbased approach to modulation classification[J].IEEE Transactions on Wireless Communications,2009,8(12):5884-5892.

