基于粒子群的产品变型设计时间预测研究

王兆华，同淑荣，黄 丽

(1.西北工业大学管理学院，陕西 西安 710072;2.江苏大学电气信息工程学院，江苏 镇江 212013)

0 引言

产品变型设计是在已有产品基础之上，为满足客户个性化需求，通过对产品的尺寸缩放、性能提升和功能扩充等方式来设计、开发新产品。其目的是针对快速变化的市场需求，迅速、高效、低成本地在原有产品基础上设计出新产品，有效缩短新产品开发周期。以往对于产品变型设计的研究主要集中在变型设计如何实现等方面［1-2］，但随着计算机辅助设计技术的飞速发展，产品变型设计实现方法日趋成熟，而变型设计中一个关键评价指标产品变型设计时间显得尤为重要。产品变型设计时间不仅关系到新产品开发周期的长短，而且直接反映出随着变型设计复杂程度的加深，与全新开发新产品相比，是否有必要进行特别复杂的产品变型改造。

目前已有学者在产品设计时间的估算和预测等方面做了一些工作。例如，文献［3］应用统计模型分析了主要的时间影响因素，建立了多变量的产品开发周期时间测量模型。文献［4］提出一种估计设计工作与时间的模型，对产品设计时间进行定量研究。文献［5］在假定产品设计活动时间服从三角分布的条件下，建立了基于仿真的复杂设计项目过程模型，可估算出项目的时间。文献［6］提出一种基于DSM 的多目标流程遗传算法来优化任务执行顺序，在假定产品开发项目中各任务时间分布的基础上，可估算出产品总的开发时间。文献［7］提出了基于高斯过程元模型的产品设计时间估计方法，考虑了产品设计时间影响因素中语言型变量，算例分析证明该方法优于模糊神经网络模型。文献［8-11］在假定设计团队、设计环境等外部因素不变，只考虑注塑模具产品特征因素的情况下，对其产品设计时间进行智能预测。

但上述研究主要集中在根据已有产品特征信息和设计时间数据，预测开发相似全新产品所需时间，而对于在原有产品基础上提升性能、增加功能的变型设计，其设计时间还鲜有研究。笔者在原有打印机基础上，通过变型设计，将其扩展为具有打印、复印、扫描等功能的一体机，对所发生的设计时间变化进行预测，提出基于tPSO-FNN 的时间预测方法。首先，通过相关度法选取与开发时间最为相关的参量构成时间因素集;其次，构建FNN 时间预测模型，并采用带极值扰动的粒子群(tPSO)算法优化时间预测模型中关键参数，连接权ω1l、隶属度函数中心值cij和宽度bij，以降低优化参数陷入局部极值的概率;最后，将该时间预测方法应用于打印机变型设计的时间预测中。

1 时间预测方法设计

1.1 确定时间因素集

影响产品变型设计所需时间的因素很多，为了使问题分析有针对性，以打印机变型设计为例，其影响因素有:打印机预热时间Pt、打印精度Pr、支持幅面Sw、复印功能Cf、扫描功能Sf、身份证复印功能Id、传真功能Ff、网络打印Np、打印速度Ps、自动双面功能Ad、自动进纸功能Af 等。这些因素与产品设计时间之间呈现高度非线性关系，很难用一个精确的数学模型来表达，人工智能方法为这类问题提供了一个有效的解决途径。在构建预测模型前，首先需要确定时间预测模型的输入集即时间因素集，该集合包含的参量不宜过多，否则会干扰预测精度，因此需要评价各影响因素与变型设计时间T 的相关度，当相关度大于或等于0.75 时可将对应参量纳入时间因素集，如表1所示。

表1 打印机变型设计时间因素集

打印机变型设计时间预测模型可描述为:在给定空间Rn(n=7)上寻找函数集合A，使得f∈A 在给定的误差约束|E|≤ε 下，有式(1)成立:

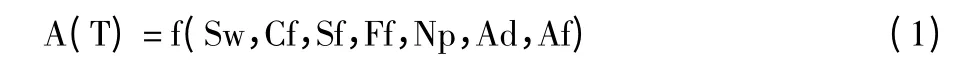
1.2 FNN 预测模型建模

图1 为打印机变型设计的模糊神经网络结构示意图，该网络分为5 层，由式(1)可知网络具有n=7个输入，分别为Sw、Cf、Sf、Ff、Np、Ad 和Af，以需要预测的打印机设计时间作为输出。

图1 模糊神经网络结构图

第1 层:输入层。

其中，xi={Sw，Cf，Sf，Ff，Np，Ad，Af}表示第i 个节点的输入值。

第2 层:模糊化层。

每个节点表示一个语言变量，如NS，PB 等，并计算隶属度函数。

其中，隶属度函数μij(xi)采用高斯函数表示的铃型函数，cij和bij分别为隶属度函数的中心和宽度，mi为分量xi对应的模糊分割数。

第3 层:规则层。

每个节点代表一条模糊规则。

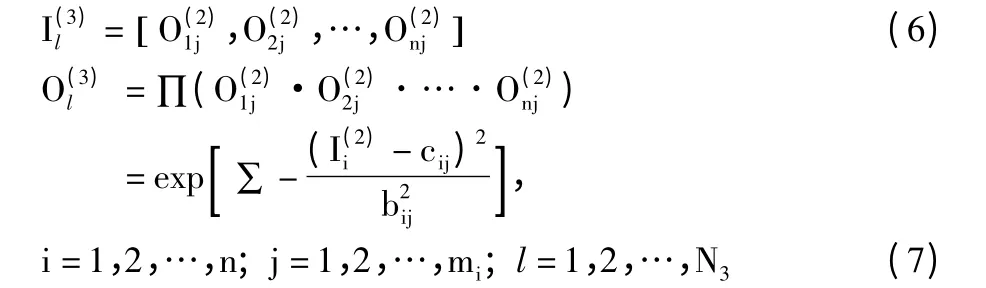
其中，N3表示可能出现的最多规则数。

第4 层:规范化处理层。

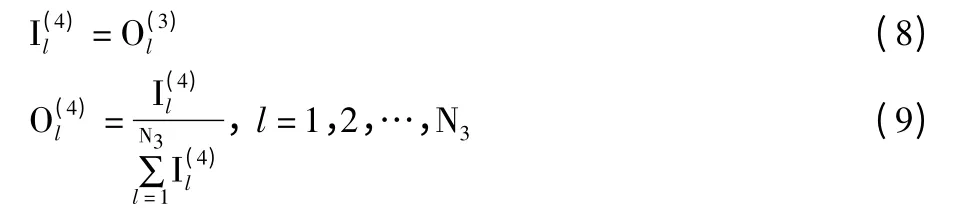
第5 层:输出层。

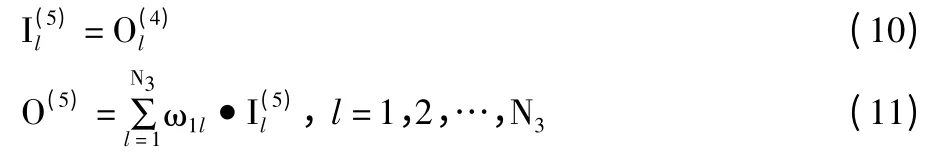
其中，ω1l为第4 层到第5 层的连接权。

1.3 tPSO 优化算法

上述打印机变型设计的模糊神经网络时间预测模型，各输入分量的模糊分割数确定时，ω1l，cij，bij这3 个参数直接影响到预测模型的拟合性能和泛化能力。粒子群(PSO)［12-13］算法具有收敛速度快、规则简单、易于实现的优点，现已成功运用于许多优化领域［14-16］。但基本PSO 算法其性能很大程度上依赖于初始参数，易陷入局部极值，进化后期收敛速度慢。而文献［17］中的极值扰动算子，用带条件的均匀随机函数值取代当前个体极值pi和全局极值pg，可以很好扰乱粒子当前搜索路径，增加粒子跳出局部极值的概率。因此采用带极值扰动的粒子群(tPSO)优化方法选取上述参量。

假设在一个D 维的目标搜索空间中，有m 个粒子组成一个群落，每个粒子被视为搜索空间中的一点，并以一定速度飞行。xi为粒子当前位置，由ω1l、cij和bij映射得到xi=［ω1l，cij，bij］i;pi为个体极值;pg为全局极值;粒子速度表示为vi。

粒子根据以下方程更新速度和位置:

其中，i=1，2，…，m;d=1，2，…，D;k 为第k 次迭代;c1，c2为非负常数，常取值为2;r1，r2为U(0，1)区间服从均匀分布的2 个独立随机数;ϖ 为惯性权重;tid，tgd分别表示pi和pg进化停滞步数;Tid，Tgd分别表示pi和pg需要扰动的停滞步数阈值。式(14)和式(15)表示带条件的均匀随机函数。

1.4 tPSO 优化模糊神经网络参数实现

tPSO 算法优化模糊神经网络时间预测模型参数，实现步骤如下:

1)根据输入、输出样本集确定模糊神经网络预估模型的拓扑结构;

2)初始化粒子群，设定粒子数m=50，加速常数c1=2、c2=1.7，最大迭代次数itermax=2000，惯性权重ϖmax=0.9，ϖmin=0.4，随机初始化r1，r2等参数，将ω1l，cij和bij映射得到xi;

3)构建模糊神经网络时间预测模型，根据式(16)计算粒子适应度值:

其中，N 为样本总数，y 为预测输出值由式(11)得到，t 为目标输出值;

4)当前粒子即pi，pg为粒子群中适应度值最小者;

5)若k ＞itmax或error ＜e，执行步骤11)，否则执行步骤6);

6)判断算法停滞步数，并根据式(14)和式(15)添加极值扰动

7)根据式(17)计算惯性权重，并由式(12)和式(13)粒子群算法更新vi和xi:

8)根据式(16)计算粒子的适应度F，再根据如下规则更新粒子的pi和pg:

若F(xi)＜F(pi)，则pi=xi;否则pi不变;

若F(pi)＜F(pg)，则pg=pi;否则pg不变。

9)停滞步数加1;

10)迭代次数k+1，返回步骤5);

11)输出pg，并将pg映射为模糊神经网络时间预测模型的ω1l，cij和bij。

2 应用实例

本文以打印机变型设计预测时间为例，根据式(1)选取Sw，Cf，Sf，Ff，Np，Ad，Af 等参量构成时间因素集，进行变型设计时间预测。网络采用5 层结构，各层节点数分别为7、21、37、37和1。经过多批次调查，剔除随机误差等，共得到83 组有效数据，将其分为2 部分，其中15%作为测试样本集，其余都作为训练样本集。

图2 为采用tPSO-FNN 打印机变型设计时间预测方法预测值与实际值的对比情况，由图可见，该tPSO-FNN 方法预测值能很好地跟踪实际值，曲线拟合程度好，说明该时间预测方法对时间的预测与真实消耗的时间基本吻合，具有较强的预测能力。

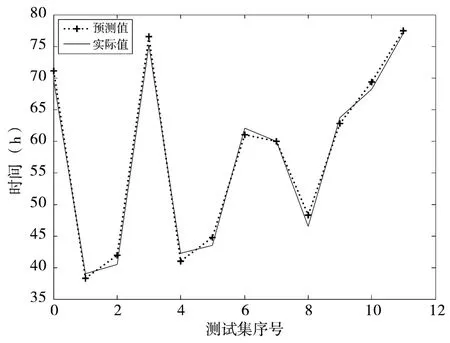
图2 tPSO-FNN 预测方法预测值与实际值对比

表2 列出了测试样本集下2 种预测方法，tPSOFNN 方法与FNN 方法的时间预测值及其误差对比情况，可知tPSO-FNN 预测方法时，时间预测的最大误差为3.93%，最小误差仅为0.02%，其平均误差为2.04%，而FNN 预测方法，时间预测的最大误差达到10.77%，最小误差为1.12%，平均误差为3.784%，都较前者偏高，主要是由于所涉及的输入变量较多，FNN 预测方法面临“维数灾难”，并且传统的FNN 是基于大样本的分析方法，泛化能力较弱，说明经过tPSO 优化后的tPSO-FNN 时间预测方法预测精度更高，泛化能力更强。

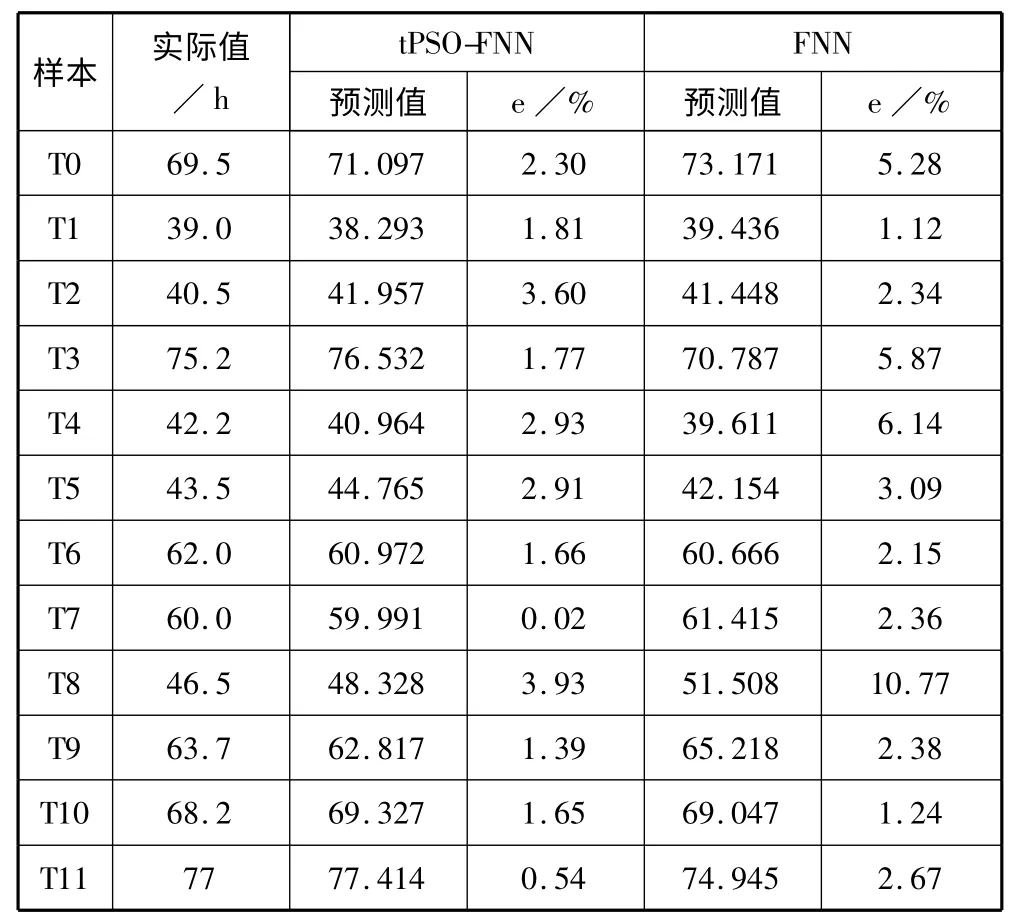
表2 预测方法误差对比

针对打印机变型设计，在不同数量训练样本下测试tPSO-FNN 预测方法的预测性能，从原有训练样本集中随机抽取其中55 组样本数据重新训练时间预测模型，并用相同的12 组测试样本集进行测试，其预测值与实际值对比情况如图3 所示，由图可知，虽然训练样本数量减少，但是该方法预测值与实际值仍然拟合较好，说明该时间预测方法仍能保持较高的精度和较强的预测能力，不会随样本数量的改变而影响变型时间预测效果，泛化性能好。

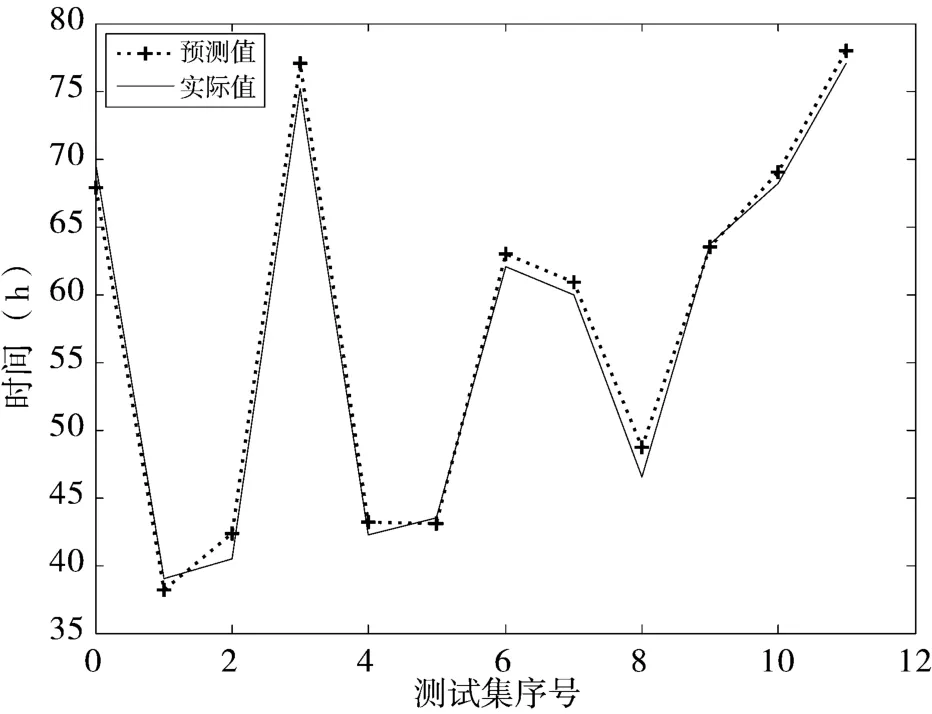
图3 55 组训练样本下tPSO-FNN 预测方法预测值与实际值对比

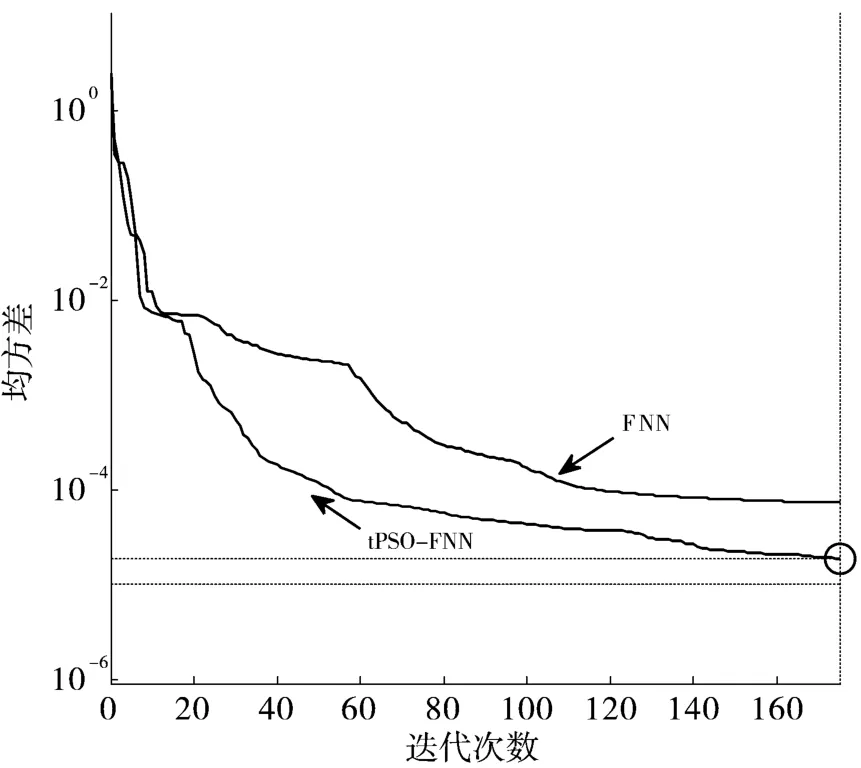
图4 误差曲线

图4 为tPSO-FNN 时间预测方法和FNN 时间预测方法下的打印机时间预测误差曲线对比，由图可见，经过175 次迭代，tPSO-FNN 时间预测方法下均方差(MSE)已经达到设定的误差范围，其值为1.8836×10-5，而FNN 时间预测方法在相同迭代次数下，MSE 只达到7.5259 ×10-5，虽然也基本满足误差要求但是较tPSO-FNN 预测方法精度略低，并且由图可见，tPSO-FNN 时间预测方法的收敛速度更快，说明tPSO 优化后的FNN 时间预测方法能够在较短的时间内获得较高的收敛精度，收敛速度和精度均优于FNN 时间预测方法，预测情况更接近实际打印机变型设计真实情况。

3 结束语

产品变型设计所需时间是产品二次开发过程关键指标之一，直接影响变型设计可行性、设计效率和设计质量。本文针对该量值难以在产品二次开发前精确预估问题，以打印机变型设计为研究对象，将粒子群算法与模糊神经网络相结合提出变型设计时间预估方法。该方法采用添加极值扰动算子的粒子群算法优化模糊神经网络参数，在避免模型陷入局部极值的同时提高收敛速度。该时间预测模型可用于预估产品变型设计过程所需时间，预测精度高，预测能力强，模型泛化性能好，同时该预测模型也为产品变型设计开发过程其他重要指标的预估提供借鉴。

［1］刘伟，曹国忠，檀润华，等.基于产品基因与物理表达的变型设计［J］.计算机集成制造系统，2015，21(2):381-391.

［2］蔡敏，胡善刚，陈丽娜，等.基于模块化方法的复杂机械产品变型设计［J］.机械设计，2013，30(4):24-28.

［3］Griffin A.Modeling and measuring product development cycle time across industries［J］.Journal of Engineering and Technology Management，1997，14(1):1-24.

［4］Bashir H A，Thomson V.Models for estimating design effort and time［J］.Design Studies，2001，22(2):141-155.

［5］Cho S H，Eppinger S D.A Simulation-based process model for managing complex design projects［J］.IEEE Transactions on Engineering Management，2005，52(3):316-328.

［6］陈冬宇，邱菀华，杨青，等.基于DSM 的复杂产品开发流程优化遗传算法［J］.控制与决策，2008，23(8):910-914.

［7］张昆仑，刘新亮，郭波.基于高斯过程元模型的产品设计时间估计方法［J］.计算机集成制造系统，2011，17(1):18-22.

［8］Xu Duo，Yan Hong-sen S.An intelligent estimation method for product design time［J］.The International Journal of Advanced Manufacturing Technology，2006，30(7):601-613.

［9］Yan Hong-Sen，Xu Duo.An approach to estimating product design time based on fuzzy υ-Support vector machine［J］.IEEE Transactions on Neural Networks，2007，18(3):721-731.

［10］商志根，严洪森.基于异方差高斯间距回归的产品设计时间预测模型［J］.系统工程学报，2013，28(4):437-445.

［11］商志根，严洪森.基于概率支持向量回归的产品设计时间预测模型［J］.计算机应用研究，2013，30(4):1099-1101.

［12］Kennedy J，Eberhart R C.Particle swarm optimization［C］// Proceedings of IEEE International Conference on Neural Networks.1995:1942-1948.

［13］Eberhart R C，Shi Y.Particle swarm optimization:Developments，applications and resources［C］// Proceedings of the 2001 Congress on Evolutionary Computation.2001:81-86.

［14］吴新生.基于粒子群算法的抄纸过程PID 神经元网络优化控制［J］.计算机与现代化，2015(3):71-74.

［15］成磊，朱龙英，郑帅等.并联机器人的粒子群优化神经网络自适应控制算法研究［J］.制造业自动化，2014，36(12):5-7.

［16］李童，毛力，吴滨.基于改进PSO 优化SVR 的交通事故预测模型［J］.计算机与现代化，2014(5):28-32.

［17］胡旺，李志蜀.一种更简化而高效的粒子群优化算法［J］.软件学报，2007，18(4):861-868.