光伏并网逆变器MLD 建模及预测控制算法

路 璐，龚仁喜，韦 潜

(广西大学电气工程学院，广西 南宁 530004)

0 引言

逆变器作为光伏并网系统的核心部件，其性能的优劣直接影响光伏系统馈入电网的电能质量。随着光伏等新能源应用日益广泛，对光伏并网逆变器的供电质量优化的研究一直是光伏并网系统研究的热点。

文献［1］在逆变器开关函数平均模型的基础上采用滞环控制的方法。此种模型是目前运用较为广泛的方法，描述了在不同开关周期电路的控制转换。在建模的过程中，将开关管作为理想的开关器件，忽略开关管的工作过程，仅将输入输出作为逆变器系统中的状态量进行讨论。但实际上，开关管通断的过程包含许多非线性和时变过程。基于此种模型的控制算法往往具有较好的静态特性，但当外界参数突变，如电网波动等情况下，逆变器的非线性特性对系统输出带来的影响更加突出，忽略了这种非线性特点的模型所对应的算法，在这种情况发生时无法快速响应外界参数的突变。

为克服建模方法对系统控制的影响，一些新的建模方法如混合逻辑动态(MLD)建模等逐渐成为对电力电子器件研究的新热点。MLD 模型是一种基于混杂系统的建模方法，将系统中存在的线性和非线性过程在一个式子中统一表达，能更准确地描述线性和非线性过程同时存在的系统。文献［2］对DC/AC 系统采用了N 步建模的方法建立DC/AC 系统的MLD 模型，将开关管工作过程分为开启、关断、跳变3 种工作状态。基于此种模型的算法在DC/DC 控制中具有较好的控制效果，但对于DC/AC 系统，由于其跟踪的输出变化较DC/DC 系统要大得多，其建模方法的预测控制处理的数据庞大，不利于硬件的实现，限制了其在实际中的运用。

本文对光伏并网逆变过程中开关器件开关状态的切换作为系统的离散事件对系统进行MLD 建模，将逆变系统视作典型的混杂系统进行分析，对逆变系统在一个输出周期内系统状态随逻辑变量变化而有规律的演化过程进行细分，对每一步演化状态进行实时的控制，提出基于MLD 此模型的预测控制算法，利用该算法能提高光伏并网系统的动态性能，对开关管对系统输出的影响进行改进，使系统输出在更短时间内满足并网的要求，简化处理过程中的数据量，更易于实际运用。通过仿真对所提模型及控制算法进行验证。

1 光伏逆变器混合逻辑动态建模

1.1 MLD 模型

MLD 模型即混合逻辑动态模型，是一种用来描述混杂系统混杂特性的模型。将混杂系统的连续过程和离散过程用统一的表达式描述。

混合逻辑动态建模是针对混杂系统通过引入逻辑变量，将系统在不同的线性过程切换中混杂特性统一表述，它对于线性和非线性过程同时存在的混杂系统的数学描述较为准确，其一般表述形式为:

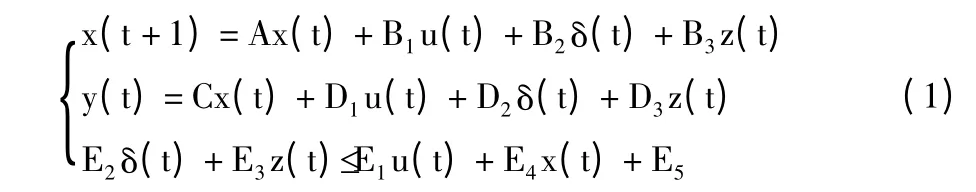
其中，x(t)为系统状态量;u(t)为系统输入控制变量;y(t)为系统输出变量;δ(t)为系统辅助逻辑变量;z(t)为辅助连续变量;A，B，C，D，E 为常系数矩阵。

MLD 模型将系统各个状态空间中的逻辑关系、切换条件以及约束条件统一在一个模型中进行分析，通过引入适当的辅助变量将系统的所遵循的逻辑规则、约束条件以及连续状态以混合逻辑不等式约束的线性方程的形式表示，从而反映各个时刻系统的状态轨迹。

1.2 光伏并网逆变器的MLD 建模

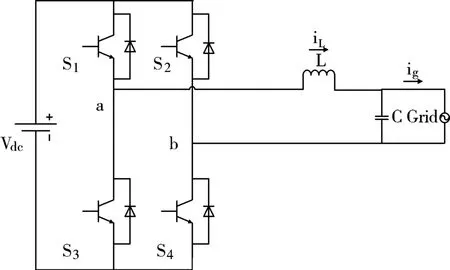
图1 光伏并网逆变器电路拓扑结构图

图1 为笔者所研究的逆变电路的拓扑结构，逆变部分使用的是全桥电路，并网部分采用LC 滤波方式。这种直接逆变器方式的拓扑结构具有较高的逆变效率，往往能达到97%以上，与传统的工频逆变方式相比，省去了笨重的变压器，使设计更加灵活，降低了成本。因此，全桥直接逆变的方式逐渐替代传统的工频逆变方式成为光伏并网逆变器设计中最广泛使用的拓扑结构。

在该系统中，输入输出电压可以看作一个线性模型，而开关管信号受驱动信号驱动产生电压脉冲序列的过程则可以看成一个典型的非线性环节。电压脉冲信号作用在电路中使电路输出连续电流。因此，光伏并网逆变器构成了由离散条件驱动连续状态演化的典型的混杂系统。

基于这一思路笔者对此电路模型进行混合逻辑动态建模:电流开关管的S1～S4的开关控制信号分别为s1～s4。其中控制信号为1 时表示开关管导通，控制信号为0 时表示开关管关断。引入逻辑运算符号“∧表示合取运算”，“∨表示析取运算”，“-表示取反运算”，“↔表示等价”［4］。对于开关管S1和S2定义电流ia流入电感的方向为正方向，引入逻辑变量σa表示电流的方向，则离散时间ia＞0 时，可用逻辑变量σa=1 表示;ia＜0 时，可用σa=0 表示，则有:

根据电路的拓扑结构可知，电路输出电压uab与开关管开关状态之间的逻辑关系为:

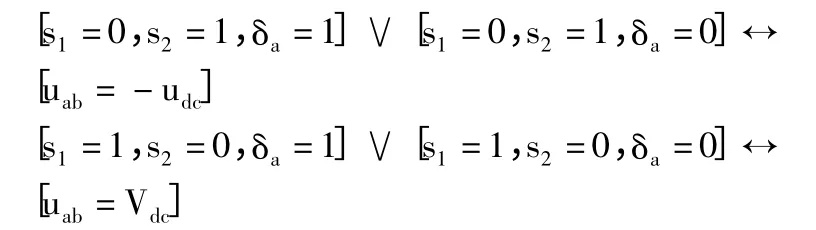
由此可知:

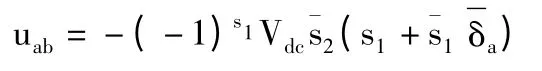
代入电路拓扑的状态方程:

可得与式(1)对应的光伏并网的MLD 模型:

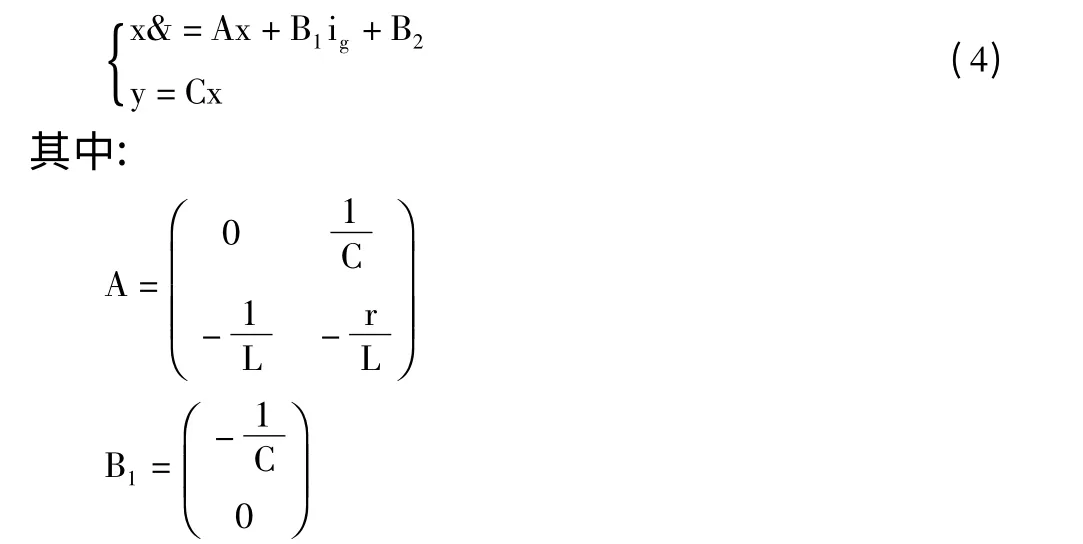
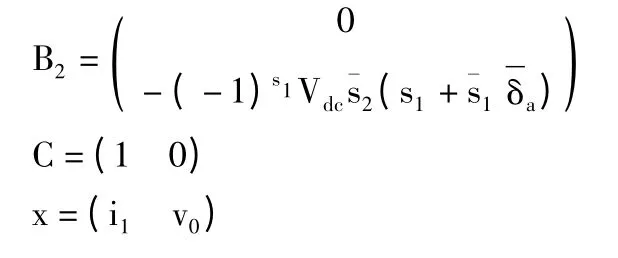
2 基于MLD 的模型预测控制算法

2.1 模型预测控制

模型预测控制主要是一种基于系统数学模型的控制策略。其中对系统精确地建模尤为重要，精确的模型能够准确地反映系统的变化。

传统的光伏并网逆变器预测控制将开关管作为理想器件，对系统一个输出周期的平均模型作为预测控制的一个单元，此种方法忽略了一个周期内开关管开关状态这一典型的非线性环节对系统输出的影响。为此采用式(4)的MLD 模型作为预测控制的预测模型，此模型由引入的开关管的通断作为系统的离散事件，受这一离散事件的推动，系统的状态量和系统输出在每一个采样周期都变得有迹可循，更为准确地描述了系统在一个周期内的参数变化。

2.2 光伏并网逆变器基于MLD 模型的预测控制

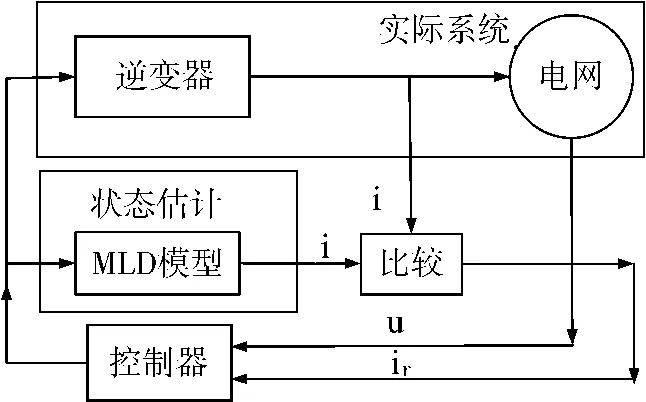
图2 逆变器混合逻辑动态模型预测控制整体框图

图2 为逆变器混合逻辑动态模型的预测控制整体框图。其具体过程是:在建立逆变器的混合逻辑动态模型的基础上，对逆变器开关管的开关状态进行估计，在每一个控制区间内控制器输出的控制量分别输入实际系统及状态估计器，比较逆变系统的实时输出与状态估计的输出，其差值作为参考信号进入控制器进行下一采样时刻的控制。由于逆变器的输出电流需要实时跟踪电网的相位变化，在每一个采样时刻需要对电网的电压进行采样输入到控制器进行锁相。

为了实现预测控制的目的，对系统的混合逻辑动体模型进行离散化处理。

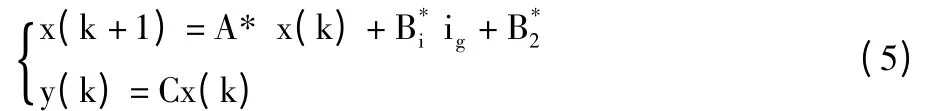
其中，A*=eAT，;TS为采样周期。

在每一个离散时间对系统进行采样，同时由控制器预测下一时刻的输出。

根据系统的历史参数预测未来参数，即对系统进行状态估计。在本设计中，需要对输出电压和输出电流进行预测，对于输出电压，根据实际的输出电压的历史参数估计未来参数，由系统的离散化方程可知，在k+1 时刻的参考输出为:

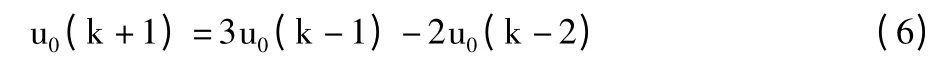
以此参数估计k +1 时刻的输出电压，而电流作为本设计的主要控制对象，由控制器根据逆变器输出信号与状态估计的比较信号作为参考输出量。

在完成系统未来时刻参数的估计后，设定优化目标函数，从而选取k+1 时刻的最优控制量，达到预测控制的目的。

为实现光伏并网发电输出电压与电网电压一致、输出电流与电网电压同频同相的目的。本文选取输出电压与输出电流作为优化的目标函数:

其中，ug为电网电压，uo为输出电压，ir为参考电流，io为实际输出电流。在k 时刻对k+1 时刻的4 种开关状态的输出分别进行计算，选取最小的g 值所对应的开关状态作为系统下一时刻的控制量输出。其流程如图3 所示。

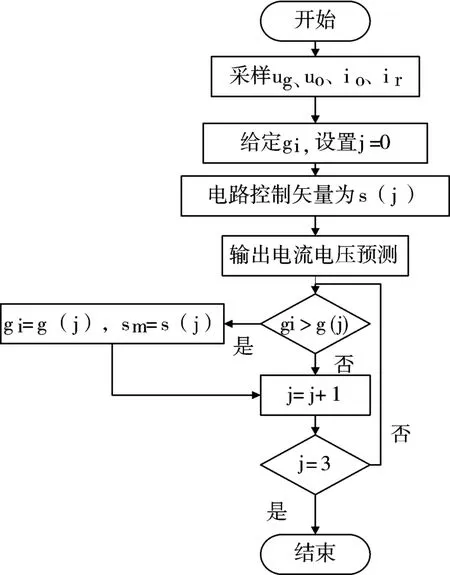
图3 预测控制流程图

系统采样k 时刻电路的各个参数:电网电压ug，输出电流io.之后为目标函数g 赋予初值gi，比较4 种不同的开关状态的输出g(j)，j=0，1，2，3，4。选取最小的g(j)所对应的开关状态sm作为系统下一时刻控制量的输出。

3 系统仿真与验证

利用Matlab/Simulink 分别对基于传统的开关函数模型的控制算法和基于MLD 模型的预测控制算法进行仿真，仿真模型如图4 所示。仿真参数为Vdc=400 V，滤波电感L=100 mL，电容C=1500 μF。

图4 逆变系统仿真模型

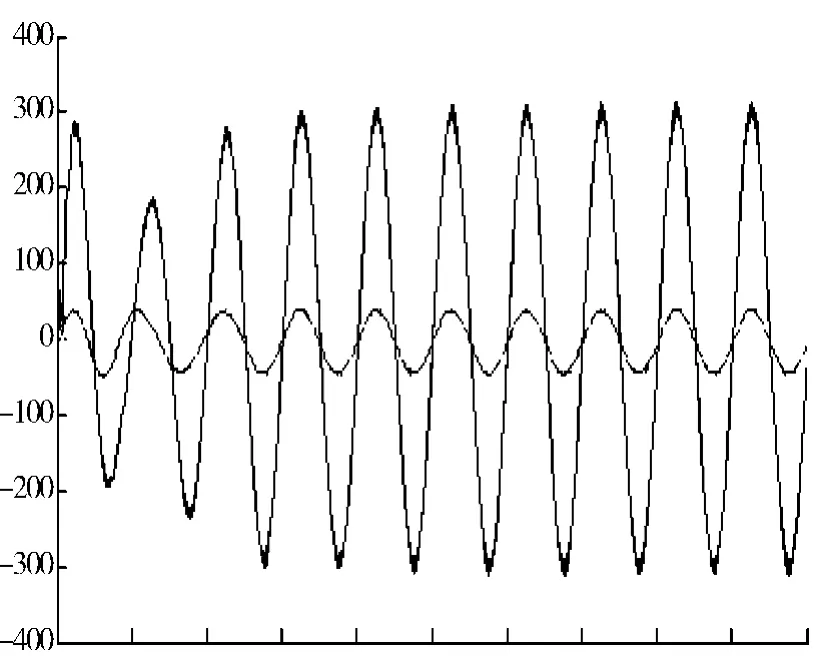
图5 开关函数平均模型的预测控制电压电流波形

图5 为基于传统开关函数平均模型的预测控制电压电流波形，可以看出在经过4 个周期以后输出电压与输出电流趋于稳定，达到了并网的要求。

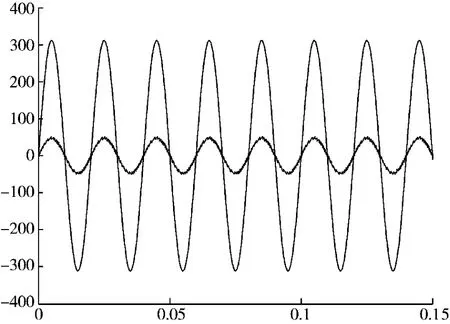
图6 基于混合逻辑动态模型网电压电流波形

图6 为基于本文提出的混合逻辑动态模型预测控制算法的电压电流波形。从第一个周期开始电流与电压的校正就已经开始在一个周期内可达到并网要求，与图4 结果相对比可以看出基于混合逻辑动态模型的预测控制有较好的动态响应，避免了逆变器反复接入电网过程对电网的影响。

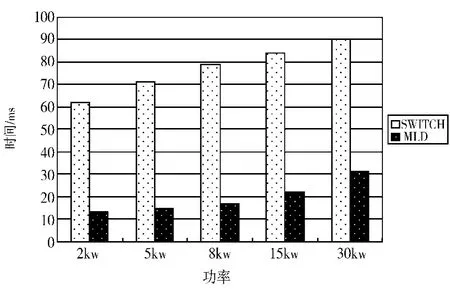
图7 逆变器在不同功率并网时间对比

图7 为逆变器工作在不同功率条件下传统开关函数模型与本文提出的MLD 模型达到并网要求时间的对比图。

根据国家标准GB/T30427-2013 中关于并网逆变器的功率因数的规定。选取当电压与电流的功率因数能稳定在0.99 之上时作为并网条件，分别对逆变器工作在2 kw～30 kw 功率时传统开关函数和MLD 模型的并网时间进行对比。从图中可以看出，MLD 模型下的预测控制方式可以更快地满足并网条件。

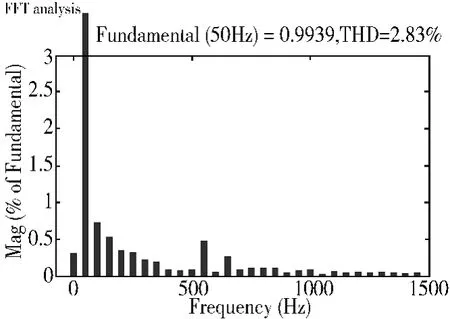
图8 输出电流谐波分析

图8 为并网输出电流30 次谐波分析，结果表明输出电流的谐波含量非常少，总谐波畸变率THD 为2.83%，满足并网要求。

4 结束语

传统基于开关函数平均模型，不论采用预测控制或是闭环控制都是对逆变器输出的一个输出周期作为控制对象进行控制，其忽略了开关器件开关状态对系统输出的影响，在实际运用中往往需要几个周期才能使电流输出波形与电网电压相位一直，达到并网条件。本文针对一个周期内系统输出随开关管的状态变化而变化的状态进行细分，建立了光伏并网逆变器的MLD 模型，并基于此模型设计了模型预测控制器，使系统电流输出更快速准确地满足并网要求。仿真结果验证了控制策略的可行性和有效性。

［1］周林，张林强，廖波，等.单相光伏逆变器控制技术研究［J］.电网技术，2012，36(9)25-30.

［2］郑雪生，李春文，戎袁杰.DC/AC 变换器的混杂系统建模及预测控制［J］.电工技术学报，2009，24(7):87-92.

［3］Axehill D，Morari M.Improved complexity analysis of branch and bound for hybrid MPC［C］// The 49th IEEE Conference on Decision and Control.2010:4216-4222.

［4］Hejri M，Giua A.Hybrid modeling and control of switching DC-DC converters via MLD systems［C］// IEEE Conference on Automation Science and Engineering.2011:714-719.

［5］安群涛.三相电机驱动系统中逆变器故障诊断与容错控制策略研究［D］.哈尔滨:哈尔滨工业大学，2011.

［6］王宝诚，郭小强，梅强，等.三相并网逆变器脱网运行电压控制技术［J］.电网技术，2011，35(7):91-95.

［7］姚志垒，王赞，肖岚，等.一种新的逆变器并网控制策略的研究［J］.中国电机工程报，2006，26(18):61-64.

［8］陈昌松，段善旭，殷进军.基于神经网络的光伏阵列发电预测模型的设计［J］.电工技术学报，2009，24(9):153-158.

［9］刘永军，万频，王东海，等.自适应模糊算法在光伏系统MPPT 中的应用［J］.太阳能学报，2008，29(6):657-661.

［10］吴丽萍.基于DSP 的光伏并网逆变系统的研究［D］.天津:河北工业大学，2007.

［11］郭小强，赵清林，邬伟扬.光伏并网发电系统孤岛检测技术［J］.电工技术学报，2007，22(4):157-162.

［12］张超，王章权，蒋燕君，等.无差拍控制在光伏并网发电系统中的应用［J］.电力电子技术，2007，41(7):3-5.

［13］范小波，张代润.光伏并网逆变器数字滞环控制的研究［J］.电力电子技术，2006，40(6):46-48.

［14］Bemporad Albert，Morari M.Control of systems integrating logic，dynamics，and constraint［J］.Automatic，1999，35(3):407-427.

［15］李秀改，高东杰，王宇红.基于混合逻辑动态模型的混杂系统预测控制［J］.控制与决策，2002，17(3):315-319.

［16］李畸勇，龚仁喜，韦海燕.滞环SVPWM 控制在光伏并网逆变器中的应用［J］.电力电子技术，2011，45(4):13-15.

［17］Bouchafaa F，Beriber D，Boucherit M S.Modeling and control of a grid connected PV generation system［C］//2010 the 18th Mediterranean Conference on Control ＆ Automation(MED).2010:315-320.