基于离散元法的立式旋耕刀结构参数对作业影响仿真分析

扈伟昊 杨发展 姜芙林 林云龙 黄珂

摘要：為探究立式旋耕刀的结构参数对其作业过程中自身受力及作业效果的影响，建立立式旋耕刀作业过程离散元模型，利用单因素试验方法，研究立式旋耕刀刀具外倾角、刀刃倾角、内折弯角对旋耕刀入土阻力、耕作阻力、扭矩、碎土率的影响，以及刀尖圆角半径对刀具入土阻力的影响。通过正交试验，研究并建立立式旋耕刀刀具外倾角、刀刃倾角和内折弯角对其所受阻力、扭矩及碎土率影响的预测模型。以减阻提效为目标，通过响应面分析和所构建的预测模型对上述3个角度参数进行优选和分析。结果表明，当刀具的外倾角为6.140°、刀刃倾角为5°、内折弯角为10.752°时，旋耕刀的耕作阻力为1 131.164 N、扭矩为307.758 N·m、碎土率为89.321%。

关键词：立式旋耕刀；结构参数；离散元法；响应面；预测模型

中图分类号：S24

文献标识码：A

文章编号：2095-5553 （2024） 05-0042-07

收稿日期：2022年9月19日  修回日期：2022年10月19日*基金项目：国家重点研发计划子课题（2018YFD0300600，2018YFD0300606）

第一作者：扈伟昊，男，1998年生，河南商丘人，硕士研究生；研究方向为立式旋耕机等。E-mail： HWH0852@163.com

通讯作者：杨发展，男，1981年生，山东郓城人，博士，教授，博导；研究方向为智能农机装备、水肥一体化装备开发等。E-mail： fazhany@163.com

Simulation analysis of effect on structural parameters of vertical rotary tiller blade

based on discrete element method

Hu Weihao， Yang Fazhan， Jiang Fulin， Lin Yunlong， Huang Ke

（College of Mechanical and Automotive Engineering， Qingdao University of Technology， Qingdao， 266520， China）

Abstract：

In order to explore the influence of structural parameters of vertical rotary tillage blade on its own stress and operation effect during operation， a discrete element model of vertical rotary tillage blade operation process was established by using single factor test method. The effects of blade bending angle， blade edge angle and necked-in blade edge on soil entry resistance， tillage resistance， torque and soil breaking rate of vertical rotary tillage blade， and the effects of blade tip fillet radii on soil entry resistance of vertical rotary tillage blade were studied. Through the orthogonal experiment，  the prediction model of the influence of the blade bending angle， blade edge angle， necked-in blade edge on the resistance， torque and soil breakage rate of vertical rotary blade was studied and established. The response surface analysis and the constructed prediction model were used to optimize and analyze the above three angle parameters with the aim of reducing drag and lifting efficiency. The obtained results showed that when the blade bending angle was 6.140°， the blade edge angle was 5°， and the necked-in blade edge angle was 10.752°. At this time， the tillage resistance of the rotary tillage cutter was 1131.164N， the torque was 307.758 N·m， and the soil crushing rate was 89.321%.

Keywords：

vertical rotary tillage blade； structural parameter; discrete element method； response surface； prediction model

0 引言

国内传统的耕地方式主要为卧式旋耕，但由于卧式旋耕的作业深度较浅，连年使用卧式旋耕会加剧犁底层的上移，进一步压缩耕层空间，不利于作物根系的发育及对养分的吸收［1-3］；在保护性耕作推行的背景下，必须改变传统的耕作模式，打破犁底层，改善作物根系生长环境，提升作物对水肥的利用率。

立式旋耕作业深度最高可达25～29 cm，可有效破碎犁底层，且与传统的卧式旋耕相比，其作业效率更高、碎土效果更好［4］，适用于大田作物、经济作物的播前耕整环节。立式旋耕直接作业部件为立式旋耕刀，由于作业深度较深，单位时间内切削扰动的土壤量较多，立式旋耕刀所受阻力和扭矩较大，其结构参数的设计直接影响整机的受力与作业效果。近年来，一些学者对立式旋耕刀的结构进行了系列的设计和研究，王英博等［5］设计了一种立式驱动浅旋耙，其刀具的刃口曲线采用最速曲线，该刃口结构可大幅提升刀具切削土壤时的滑切效果；杨硕［6］设计了一种桑园动力耙，研究发现该机具安装的旋耕刀外倾角（即立式旋耕刀内折弯角）过小或过大都会使旋耕刀所受的扭矩增大。国内学者对立式旋耕刀结构的研究大多依托于立式旋耕机，很少将其视为直接的研究对象。

离散元法目前被认为是一种适用于不连续介質力学行为预测和分析的方法，最初由Cundall等［7］提出，目前已广泛应用于各工、农业领域。刘立晶等［8］利用离散元法对其设计的带状深松全层施肥铲进行了仿真试验，得到的相关预测模型的误差较小；Shaikh等［9］利用离散元法研究了履带链板在不同含水率土壤条件下产生牵引力的大小，仿真结果的最小误差为10.09%；邓佳玉［10］使用EDEM对深松铲作业过程的受力情况进行仿真分析，结果表明仿真值与试验值相差5%～15%。

本文通过离散元法研究立式旋耕刀的结构参数（刀具外倾角、刀刃倾角、内折弯角和刀尖圆角半径）对立式旋耕作业的影响，并进一步通过正交试验对立式旋耕刀的结构参数进行优化设计。

1 仿真模型建立

1.1 立式旋耕刀结构参数及模型建立

刀具外倾角可以提高旋耕刀单转子的作业面积，调整刀具的外倾角可在立式旋耕机相邻两转子轴距不变的情况下改变他们间的作业重合区域的大小，避免产生漏耕现象，且土壤破碎均匀；刀刃倾角可以减小刀具入土时的阻力，在刀具宽度不变的情况下，刀刃倾角会减小刀具的作用面积，从而对旋耕刀的受力和碎土效果产生影响；立式旋耕刀作业时，其绝对运动为绕转轴转动与随机具前进合成的余摆线运动，若刀具没有设置内折弯角，旋耕刀作业时刀背与土壤之间会产生“抗土”现象，导致刀具所受的阻力和机组的振动大幅增加，降低机组的稳定性与可靠性，但过大的内折弯角又会增大切削角，提高切削难度［3］；在旋耕刀的刀尖作圆角处理可使刀具的入土过程更加顺畅，圆角半径对作业过程的具体影响则通过仿真试验确定。

本试验中立式旋耕刀的材料为65Mn，为保证旋耕刀的整体强度，刀片的厚度设置为10 mm，刀刃宽度为5 mm；旋耕刀的耕深适用范围为200～250 mm，刀刃线长度设置为260 mm，刀身宽度70 mm，刀具的结构参数如图1所示。利用SolidWorks软件建立立式旋耕刀的三维模型，以.igs格式保存，以便后续导入EDEM离散元软件中。

1.2 土槽模型建立

通过显微镜观察驻地农田采集到的土壤颗粒，发现土壤颗粒多呈球形或片状，因此在EDEM中将土壤颗粒简化为球形（Single Sphere）与三球组合的片状颗粒（Triple Sphere）；通过土壤的粒径分析试验，测得土壤的颗粒的平均直径为0.52 mm，为减小计算量，查阅文献后，将仿真模型中单个球形颗粒的半径放大至5 mm。土壤颗粒实际形貌及仿真土壤颗粒如图2所示。

土壤颗粒间的接触模型选择Hertz-Mindlin with Bonding，该模型在颗粒之间形成Bond键以承受一定的阻力和阻力矩，Bond键所受法向力与切向力达到临界值时发生断裂该模型在颗粒之间形成黏结键以承受一定的阻力和阻力矩［11， 12］，黏结键产生之后，颗粒上的法向力Fn、切向力Ft与法向力矩Tn、切向力矩Tt从0随时间步按照式（1）调整。

2 单因素试验结果分析

2.1 刀具外倾角对旋耕刀作业过程的影响

本试验中设置旋耕刀的刀具外倾角分别为0°、5°和10°，导入土槽后，获得不同刀具外倾角旋耕刀所受的阻力、扭矩及Bond键的破碎情况如表2所示。

表2中，旋耕刀入土阻力值取0～0.23 s时间段内的平均受力，阻力、扭矩取其第二个旋转周期的平均值，碎土率为立式旋耕作业1 m区域内破损的Bond键占总键数量的百分比（后续仿真取值方式与此相同）。

由表2可知，当旋耕刀的外倾角从0°变为5°时，入土阻力有减小的趋势，但当其增大至10°时，入土阻力从472.77 N增加到568.59 N，这可能是由旋耕刀内侧对土壤的挤压作用产生的阻力变大的原因造成的；另外，随着刀具外倾角的增大，旋耕刀作业时所受的阻力逐渐减小，扭矩逐渐增大，由于作业面积增大，Bond键破碎数量增加，而碎土率的变动在1%内，影响并不明显。

2.2 刀刃倾角对旋耕刀作业过程的影响

建立的旋耕刀的刀刃倾角分别为0°、2.5°及5°，将其导入至土槽模型进行仿真，经数据处理后得到的刀刃倾角对旋耕刀作业的影响如表3所示。

从表3可以看出，随着刀刃倾角的增大，旋耕刀的入土阻力、作业时所受阻力及扭矩都有明显的下降，Bond键破碎数下降了37 867个和28 171个，碎土率下降0.59%和2.81%。这主要是因为增大刀刃倾角会使整个刀片宽度减小，刀具的体积减小，降低其受力及扭矩，也降低其对土壤的扰动能力。

2.3 内折弯角对旋耕刀作业过程的影响

仿真试验设置0°、10°和20°三种内折弯角水平的旋耕刀，并将其引入仿真土槽试验，数据处理之后获得内折弯角对旋耕刀作业的影响如表4所示。由表4可知，在0～20°范围内随着内折弯角的增加，旋耕刀入土阻力有所增大，耕作过程中所受阻力明显减小，扭矩由343.25 N·m下降至330.81 N·m后有所提升；Bond键破碎数增多，碎土率呈增大趋势，但变化很小。

2.4 刀尖圆角半径对旋耕刀作业过程的影响

为探究圆角半径大小对入土阻力及刀具作业过程的影响，设计单因素试验，试验中设置圆角半径分别为0 cm、3 cm、4 cm和5 cm的四把旋耕刀，仿真試验结果如表5所示。

由表5可知，刀尖做圆角处理可有效减小刀具入土时受到的阻力，且在试验选取的0～5 cm的半径取值范围内，入土阻力随着刀尖圆角半径的增大逐渐减小；但在旋耕作业过程中，圆角半径的变化对旋耕刀所受的阻力、扭矩及其碎土效果的影响并不明显。

3 正交试验设计与结果分析

3.1 试验设计与结果

由单因素试验可知，立式旋耕刀的刀具外倾角、刀刃倾角、内折弯角对刀具受到的载荷和及其碎土效果有较大的影响，刀尖圆角半径在降低刀具入土阻力上效果较明显，对旋耕作业过程的影响不大。因此，选取刀具外倾角、刀刃倾角、内折弯角作为仿真试验因素，以旋耕刀作业过程中所受阻力、扭矩及碎土率作为评价指标，利用Design-Expert 12软件设计基于Box-Behnken原理的三因素三水平正交试验对上述三个结构参数进行优化分析［16］，试验刀具的因素水平编码如表6所示，刀尖圆角半径均设置为4 cm。试验结果如表7所示。

3.2 试验结果分析

1） 耕作阻力的回归模型建立与响应面分析。

对立式旋耕刀耕作阻力做二次回归分析，得到响应曲面回归模型如式（3）所示。

F=

1 248.43-54.86A-91.59B-147.84C-21.75AB-31.97AC+46.01BC

（3）

对模型进行显著性分析及可信度分析如表8、表9所示。由表8可知，模型的P值小于0.000 1，远小于0.05，该数值说明模型极显著，可在设计中用于耕作阻力的预测。因素A、B、C对耕作阻力的影响极为显著，BC项显著，AB、AC项较为显著各参数的二次项A2、B2、C2不显著，已从模型中剔除。由表9可知，模型的复相关系数为0.984 5，信噪比为38.518 3，表明该模型与实际模拟较好，可信度较高。

从图3可知，在试验选取的取值范围内，刀具外倾角A、刀刃倾角B、内折弯角C的增加都会降低立式旋耕刀耕作过程中所受阻力，这与单因素试验结果相一致；由图3（a）可知，不考虑内折弯角情况下，单独提高刀刃倾角和刀具外倾角的值对耕作阻力的减小并不显著；由图3（b）可知，当内折弯角取值较小时，单独增大旋耕刀外倾角的降阻效果并不显著，随着内折弯角度数的增加，提高刀具外倾角的降阻效果逐渐趋于显著；由图3（c）可知，同时增加内折弯角和刀刃倾角的降阻效果显著。

2） 扭矩的回归模型建立与响应面分析。

经Design-Expert软件处理数据后得到扭矩的二次回归模型如式（4）所示。

T=

3.291 2+19.41A-30.61B-24.31C-

8.07AB+12.53BC+7.56B2

（4）

该模型的方差分析及可靠性分析如表10、表11所示。扭矩回归模型的方差分析结果表明，该模型的P值小于0.000 1，表明该模型的显著性极高，信噪比为24.729 5远大于4，说明该模型可以用来指导设计。从表中各因素的P值可知，三个一阶因素A、B、C的显著性都极高，交互项BC较为显著，交互项AB和二阶刀刃倾角B2显著。

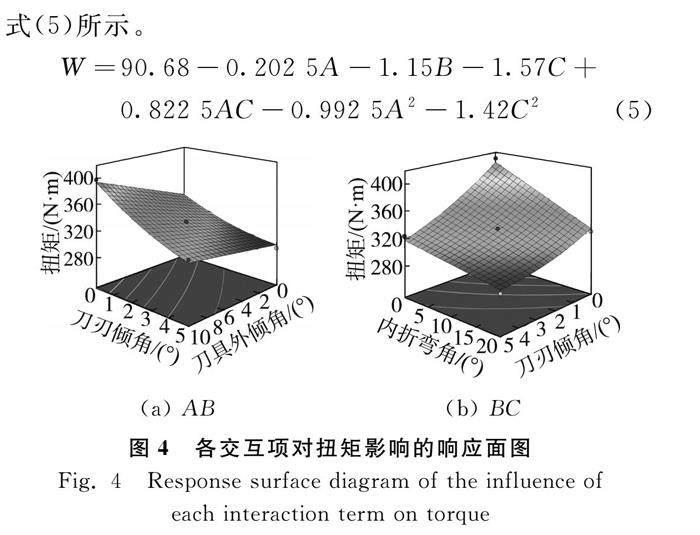
图4为交互项AB、BC的响应曲面图，从图4中可知，同时增大内折弯角和刀刃倾角可有效减小扭矩；在内折弯角不变的情况下，增加刀刃倾角，减小刀具外倾角的度数也可降低扭矩。

3） 碎土率的回归模型建立与响应面分析。

经过数据分析，得到三个因素对碎土率影响的回归模型如式（5）所示。

W=

90.68-0.202 5A-1.15B-1.57C+

0.822 5AC-0.992 5A2-1.42C2

（5）

对该模型进行方差和可信度的分析，结果如表12、表13所示。从表12可知，模型整体P值小于0.000 1远小于0.05，表明该碎土率回归模型显著性很高；失拟向P=0.470 9＞0.05，表明该模型的预测结果与实际结果拟合效果好，由表13可知，模型的复相关系数为0.967 2，信噪比为23.119 1，表明该模型的可靠性较高。观察各影响因素的P值可知，刀具外倾角A对碎土率的影响并不显著，而刀刃倾角B、内折弯角C有极高的显著性，二阶内折弯角C2也极为显著，二阶刀具外倾角A2也有较高的显著性，交互项AC显著性最低，其他二次项或交互项的显著性较差，已从模型中删除。

图5为交互项AC的等高线图及响应曲面图，从图5中可知在一定范围内，减小内折弯角C和刀具外倾角A可提高立式旋耕刀碎土率。但当刀具外倾角A取值接近0°时又会使碎土率呈现下降的趋势。

3.3 参数优选

通过Design-Expert参数优化模块，对A、B、C三个参数进行优化设计，优化目标、约束条件及权重如表14所示，表中权重代表该参数的重要性，参数权重“+”的数量越多表示该参数在优化设计中的优先级越高。

经过优化求解，获得结果为：刀具外倾角A为6.140°，刀刃倾角B为5°，内折弯角C为10.752°，此时的耕作阻力为1 131.16 N，扭矩为307.76 N·m，碎土率为89.32%。

4 结论

利用离散元软件EDEM建立立式旋耕刀作业过程的仿真模型，设计单因素试验与正交试验对立式旋耕刀结构参数进行分析与优化。

1）  确定各旋耕刀的入土阻力、耕作阻力、扭矩、碎土效果随各参数改变的变化趋势。

2）  获得立式旋耕刀作业过程中所受阻力、扭矩及碎土率的预测模型；获得立式旋耕刀外倾角、刀刃倾角及内折弯角等因素对上述三个指标影响的显著性。

3）  通过Design-Expert软件参数优化模块，以降低耕作阻力为主要目的，保证碎土率不低于国标要求85%，优选出一组立式旋耕刀结构参数：刀具外倾角6.140°、刀刃倾角5°、内折弯角10.752°，代入预测模型得到耕作阻力为1 131.16 N，扭矩为307.76 N·m，碎土率为89.32%。

参 考 文 献

［1］ 翟振， 李玉义， 逄焕成， 等. 黄淮海北部农田犁底层现状及其特征［J］. 中国农业科学， 2016， 49（12）： 2322-2332.

Zhai Zhen， Li Yuyi， Pang Huancheng， et al. Study on present situation and characteristics of plow pan in the northern region of Huang Huai Hai Plain ［J］. Scientia Agricultura Sinica， 2016， 49（12）： 2322-2332.

［2］ 杨世琦， 吴会军， 韩瑞芸， 等. 农田土壤紧实度研究进展［J］. 土壤通报， 2016， 47（1）： 226-232.

Yang Shiqi， Wu Huijun， Han Ruiyun， et al. A review of soil compaction in farmland ［J］. Chinese Journal of Soil Science， 2016， 47（1）： 226-232.

［3］ 白伟， 孙占祥， 郑家明， 等. 辽西地区土壤耕层及养分状况调查分析［J］. 土壤， 2011， 43（5）： 714-719.

Bai Wei， Sun Zhanxiang， Zheng Jiaming. Soil plough layers and soil nutrients in Western Liaoning ［J］. Soils， 2011， 43（5）： 714-719.

［4］ 第一機械部机械研究院. 农业机械设计手册［M］. 北京： 机械工业出版社， 1973.

［5］ 王英博， 荣高， 李洪文， 等. 立式驱动浅旋耙设计与参数优化［J］. 农业工程学报， 2019， 35（9）： 38-47.

Wang Yingbo， Rong Gao， Li Hongwen， et al. Design and parameter optimization of vertical driving-type surface rotary tillage machine ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2019， 35（9）： 38-47.

［6］ 杨硕. 桑园动力耙的优化设计与试验［D］. 泰安： 山东农业大学， 2020.

Yang Shuo. Optimal design and experimental on rotary harrow in mulberry field ［D］. Taian： Shandong Agricultural University， 2020.

［7］ Cundall P A， Strack O D L. A discrete numerical model for granular assemblies ［J］. Géotechnique， 1979， 29（1）： 47-65.

［8］ 刘立晶， 马超， 刘忠军. 基于EDEM的带状深松全层施肥铲作业参数优化与试验［J］. 农业机械学报， 2021， 52（10）： 74-83.

Liu Lijing， Ma Chao， Liu Zhongjun. EDEM-based parameter optimization and experiment of full-layer fertilization shovel for strip subsoiling ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2021， 52（10）： 74-83.

［9］ Shaikh S A， Li Yaoming， Ma Zheng， et al. Discrete element method （DEM） simulation of single grouser shoe-soil interaction at varied moisture contents ［J］. Computers and Electronics in Agriculture， 2021， 191（1-2）： 106538

［10］ 邓佳玉. 基于离散元法的深松铲耕作阻力的仿真与试验研究［D］. 大庆： 黑龙江八一农垦大学， 2015.

Deng Jiayu. Simulation and experimental study of the subsoiler tillage resistance based on discrete element method ［D］. Daqing： Heilongjiang Bayi Agricultural University， 2015.

［11］ 刘坤宇， 苏宏杰， 李飞宇， 等. 基于响应曲面法的土壤离散元模型的参数标定研究［J］. 中国农机化学报， 2021， 42（9）： 143-149.

Liu Kunyu， Su Hongjie， Li Feiyu， et al. Research on parameter calibration of soil discrete element model based on response surface method ［J］. Journal of Chinese Agricultural Mechanization， 2021， 42（9）： 143-149.

［12］ 方会敏， 姬长英， 张庆怡， 等. 基于离散元法的旋耕刀受力分析［J］. 农业工程学报， 2016， 32（21）： 54-59.

Fang Huimin， Ji Changying， Zhang Qingyi， et al. Force analysis of rotary blade based on distinct element method ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2016， 32（21）： 54-59.

［13］ 祝英豪， 夏俊芳， 曾榮， 等. 基于离散元的稻板田旋耕功耗预测模型研究［J］. 农业机械学报， 2020， 51（10）： 42-50.

Zhu Yinghao， Xia Junfang， Zeng Rong， et al.Prediction model of rotary tillage power consumption in paddy stubble field based on discrete element method ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2020， 51（10）： 42-50.

［14］ 王燕. 基于离散元法的深松铲结构与松土效果研究［D］. 长春： 吉林农业大学， 2014.

Wang Yan. Simulation analysis of structure and effect of the subsoiler based on DEM ［D］. Changchun： Jilin Agricultural University， 2014.

［15］ 王学振， 岳斌， 高喜杰， 等. 深松铲不同翼铲安装高度时土壤扰动行为仿真与试验［J］. 农业机械学报， 2018， 49（10）： 124-136.

Wang Xuezhen， Yue Bin， Gao Xijie， et al. Discrete element simulations and experiments of disturbance behavior as affected by mounting height of subsoiler swing ［J］. Transactions of the Chinese Society for Agricultural Machinery， 2018， 49（10）： 124-136.

［16］ 张敏， 金诚谦， 梁苏宁， 等. 风筛选式油菜联合收割机清选机构参数优化与试验［J］. 农业工程学报， 2015， 31（24）： 8-15.

Zhang Min， Jin Chengqian， Liang Suning， et al. Parameter optimization and experiment on air-screen cleaning device of rapeseed combine harvester ［J］. Transactions of the Chinese Society of Agricultural Engineering， 2015， 31（24）： 8-15.