数轴上的动点问题的解法研究

方成

【摘要】数轴上动点问题是初一数学的一种重要题型，经常作为压轴题出现.动点问题蕴含着丰富的数形结合、分类转化的思想方法，对学生处理信息并转化为数学模型的能力要求较高.关于如何解决数轴上动点问题，本文有一些思考和建议，期望能对大家有所帮助.

【关键词】初中数学；数轴；动点；解题技巧

一直以来，动点问题都是中考中的重点题型，它通常是由一个大问题组成，再细化成一个个小问题.需要学生层层抽丝剥茧，由浅入深地挖掘题目中的核心条件.数轴是学生进入初中以来第一次数与形的碰撞，借助数轴感受“化数为形，化形为数”.动点问题在数轴上的应用具有明显的综合性，它融合了行程的概念、数与形的结合，以及分类转化的思维方式.对这类问题解法研究应做到由易到难，分类时不重不漏，有理有据.

1 理清基础知识

1.1 一个动点平移

在一条数轴上，我们规定向右为正，向左为负.如果一个点向右平移，只需要把这个点加上运动的距离.如果向左运动，就是减去它运动的距离.

（1）如图1，假设点P位于原点，那么向右移动3个单位长度后达到的点A，其所代表的数值可以理解为0加上3，即3；向左移动3个单位长度得到点B，则点B代表的数值理解为0减去3，即－3.

（2）设定点P代表的数是2，当其向右移动3个单位长度后，我们得到点A，此时，点A所表达的数值可以被认为是5，这是由2加3计算得出的；向左移动3个单位长度到点B，点B所表达的数值可以被认为是-1，这是由2减去3计算得出的－1.

1.2 两点距离

如图2，点E与点F的距离，即线段EF的长.

（1）若点E所表示的数为2，点F所表示的数为5，则EF=5－2=3；

（2）若点E所表示的数为-2，点F所示的数为3，则EF=3－（－2）=5；

（3）若点E所表示的数为-2，点F所示的数为-4，则EF=－2－（－4）=2.

根据以上分析，我们可以得出：在数轴上，两点之间的距离等于这两点所对应的坐标差的绝对值，也就是右侧的数值减去左侧的数值.这个原则可以简单地概括为“大数减小数”.归纳可得：若点E所表示的数为a时，点F所示的数为b，且a>b，则EF=a－b；若点E所表示的数为a时，点F所示的数为b，则EF=a－b.

1.3 中點表示法

如图3，数轴上点P向左移动2个单位长度到点F表示的数为-1，向右移动2个单位长度到点E表示的数为3，则点P表示的数是1.由此可得，数轴上点E表示的数为a，点F表示的数为b，那么线段EF的中点P表示数为a+b2.

1.4 行程问题

当动点在数轴上移动时，我们可以将向右的移动方向定义为正方向，并将向右的移动速度定义为正速度，反之，向左的移动速度则被视为负速度.从这个角度来看，我们可以通过在起点的基础上增加该点的移动距离确定其移动后的坐标.

2 剖析典型例题

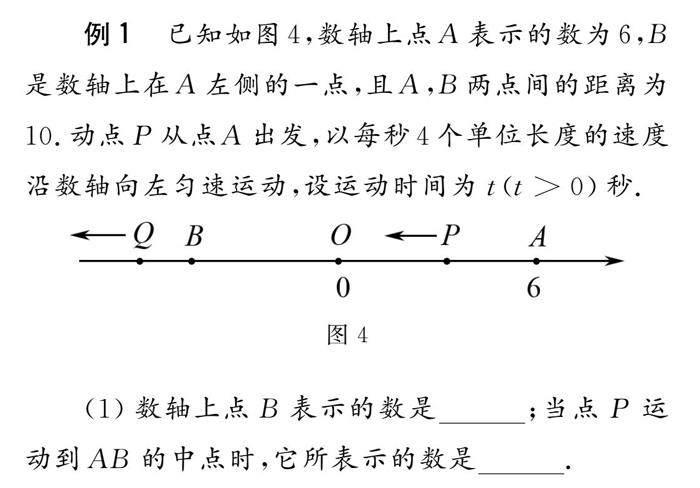
例1 已知如图4，数轴上点A表示的数为6，B是数轴上在A左侧的一点，且A，B两点间的距离为10．动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为tt>0秒．

（1）数轴上点B表示的数是；当点P运动到AB的中点时，它所表示的数是．

（2）动点Q从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P，Q同时出发．求：

①当点P运动多少秒时，点P追上点Q？

②当点P运动多少秒时，点P与点Q间的距离为8个单位长度？

解析 （1）运用点的平移，B在A左边，A表示的数为6，A，B两点间的距离为10，所以数轴上点B所表示的数为6－10=－4；P运动到AB中点，是（－4+6）÷2=1.

（2）采用方程解决此类问题，这题是行程问题中的同向追赶问题.①点P运动t秒时追上点Q，由于点P要多运动10个单位才能追上点Q，则4t=10+2t，然后解方程得到t＝5；②分两种情况：当点P运动a秒时，不超过Q，则10+2a－4a=8；超过Q，则10+2a+8=4a；由此求解即可.

①点P运动t秒时追上点Q根据题意得4t=10+2t，解得t＝5.

答：当点P运动5秒时，点P追上点Q.

②设当点P运动a秒时，点P与点Q间的距离为8个单位长度，当P不超过Q，则10＋2a-4a＝8，解得a＝1；当P超过Q，则10+2a+8=4a，解得a=9.

答：当点P运动1或9秒时，点P与点Q间的距离为8个单位长度.

因此，解决数轴上动点问题的思想方法是含有字母的代数式表示动点的位置，再运用分类讨论思想和已知条件来列方程计算．

3 明确解题思路

动点问题的解题思想是数形结合，分类转化.著名数学家华罗庚说过：“数缺形时少直观，形少数时难入微，数形结合百般好，隔离分家万事休.”简而言之，就是在动点数学问题中要将数量关系和空间形式相结合，加以处理.

解决动点问题的第一步，审题，直接剖析问题核心，抓住动点，理清题目，画出图形，在多个条件中提取关键信息；第二步，在数轴上表示各点的坐标，并理清动点速度，时间和路程；第三步，动点在数轴上所表示的数用字母表示；第四步，借助数轴上线段长度、线段中点的代数表示方法，根据题目列出方程，并解方程.这样就归纳出数轴上的动点问题的“通性通法”，从而帮助学生化难为易，化动为静，分类讨论，抓住动点用代数表示，以不变应万变，寻找破题点.

理想的数学解题，教师应该认真思考自己所要传授的数学知识点，洞穿这一知识点处于相关知识结构的环节之中，确定知识环节的来龙去脉，还要细心分析学生生成这一知识点时的心理环节，发现学生生成知识的“来龙”与“去脉”之间的本质差异［1］.数学学习的过程就是已有基础知识的建构，生成新的知识结构，实现知识的“再生长”，从而从解题中萌生数学的思想方法，激发学生学习数学的热情.

参考文献：

［1］张昆，宋乃庆.初一列方程入门教学的思考与建议［J］.中学数学杂志，2014（02）：4-7.