函数视角下的一道数列不等式问题的多解与推广

陈杰 高成龙

1.试题呈现

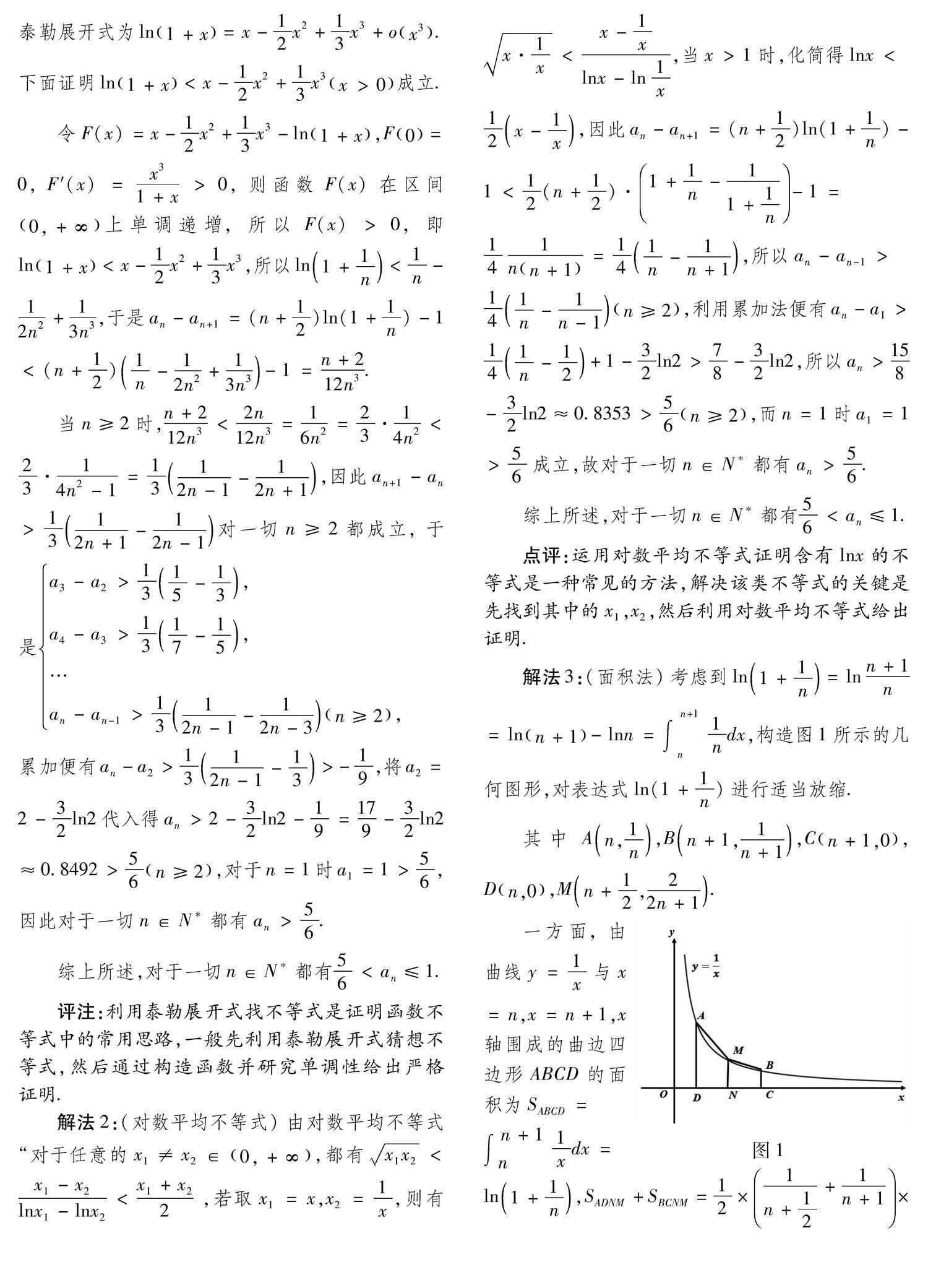
题目（2023年天津卷20题）已知函数f（x）=1x+12lnx+1．（1）求曲线y=f（x）在x=2处切线的斜率；（2）当x>0时，证明：f（x）>1；（3）证明：56

题目（1）（2）比较简单，本文不作讨论.对于（3）题，设an=lnn！－n+12lnn+n，解决该问题的关键有两个步骤：第一，考虑到a1=1，不等式右半部分只需要证明数列an关于n单调递减即可；第二，由于 an－an+1=－1+n+12ln1+1n=bn，利用不等关系对数列bn进行适当的放缩，将其转化为一个可求和的数列，然后利用累加法得到an>56.

2.解法探究

（1）（2）略；（3）设an=lnn！－n+12lnn+n，n∈N，则an－an+1=（n+12）ln（1+1n）－1=f1n－1>0，于是数列an关于n单调递减且a1=1，所以an≤a1=1，n∈N成立.下面用五种方法来证明不等式左半部分.

解法1：（泰勒展开）由于函数y=ln1+x的泰勒展开式为ln1+x=x－12x2+13x3+ox3.下面证明ln1+x0成立.

令F（x）=x－12x2+13x3－ln1+x，F0=0， F′（x）=x31+x>0，则函数F（x）在区间0，+∞上单调递增，所以F（x）>0，即ln1+x

所以ln1+1n<1n－12n2+13n3，于是an－an+1=（n+12）ln（1+1n）－1<（n+12）1n－12n2+13n3－1=n+212n3.

当n≥2时，n+212n3<2n12n3=16n2=23·14n2<23·14n2－1=1312n－1－12n+1，

因此an+1－an>1312n+1－12n－1对一切n≥2都成立， 于是

a3－a2>1315－13，

a4－a3>1317－15，

…

an－an－1>1312n－1－12n－3n≥2， 累加便有an－a2>1312n－1－13>－19，将a2=2－32ln2代入得an>2－32ln2－19=179－32ln2≈0.8492>56n≥2，对于n=1时a1=1>56，

因此对于一切n∈N都有an>56.综上所述，对于一切n∈N都有56

评注：利用泰勒展开式找不等式是证明函数不等式中的常用思路，一般先利用泰勒展开式猜想不等式，然后通过构造函数并研究单调性给出严格证明.

解法2：（对数平均不等式）由对数平均不等式“对于任意的x1≠x2∈0，+∞，都有x1x21时，化简得lnx<12x－1x，因此an－an+1=（n+12）ln（1+1n）－1<12（n+12）·1+1n－11+1n－1=141nn+1=141n－1n+1，所以an－an－1>141n－1n－1n≥2，利用累加法便有an－a1>141n－12+1－32ln2>78－32ln2，所以an>158－32ln2≈0.8353>56n≥2，而n=1时a1=1>56成立，故对于一切n∈N都有an>56.

综上所述，对于一切n∈N都有56

点评：运用对数平均不等式证明含有lnx的不等式是一种常见的方法，解决该类不等式的关键是先找到其中的x1，x2，然后利用对数平均不等式给出证明.

解法3：（面积法）考虑到ln1+1n=lnn+1n=lnn+1－lnn=∫n+1n  1ndx，构造图1所示的几何图形，对表达式ln（1+1n）进行适当放缩.

其中An，1n，Bn+1，1n+1，Cn+1，0，Dn，0，Mn+12，22n+1.

图1

一方面，由曲线y=1x与x=n，x=n+1，x轴围成的曲边四边形ABCD的面积为SABCD=∫n+1

n     1xdx=ln1+1n，

SADNM+SBCNM=12×1n+12+1n+1×12+12×1n+12+1n+1×12=1442n+1+1n+1n+1，

由图可知SABCD

因此an+1－an>181n+1－1n对一切n∈N都成立，利用累加法便有an－1>181n－1n≥2，所以an>18n+78>78n≥2，又 a1=1>78，因此，對于一切n∈N n∈N都有56

点评：该法的关键是利用曲线y=1x构造曲边四边形并利用面积的不等关系对ln1+1n进行放缩，进而将an－an+1=（n+12）ln（1+1n）－1放缩成一个可以求和的数列，进而运用累加法得到不等式左半部分的证明.

解法4：（构造函数法）由解法3的分析，我们只需要证明不等ln（1+1n）<1442n+1+1n+1n+1n∈N.

于是构造函数F（x）=ln（1+x）－144xx+2+x+xx+1，F0=0， F′（x）=11+x－148x+22+1+1x+12=－x2x2+2x+24x+12x+22<0.

所以F（x）在区间0，+∞上单调递减，因此F（x）<0在区间0，+∞上恒成立，所以F1n=ln（1+1n）－1442n+1+1n+1n+1<0，即ln（1+1n）<1442n+1+1n+1n+1n∈N，

所以an－an+1=（n+12）ln（1+1n）－1<1442n+1+1n+1n+1·（n+12）－1=181n－1n+1.

因此an+1－an>181n+1－1n对一切n∈N都成立， 累加得an－1>181n－1n≥2，所以an>18n+78>78n≥2， a1=1>78，因此对一切n∈N都有an>78>56.

解法5：（构造函数法）由题目要证明的不等式是56

构造函数F（x）=ln（1+x）－13x3+6x2+6xx+12x>0，F0=0 F′（x）=－x3－33x+13<0，所以F（x）在区间0，+∞上单调递减，因此F（x）<0在区间0，+∞上恒成立，所以n+12ln（1+1n）－1－161n－1n+1<0，即n+12ln（1+1n）－1<161n－1n+1（n∈N）.

所以an－an+1=（n+12）ln（1+1n）－1<161n－1n+1n∈N，即an+1－an>161n+1－1nn∈N，于是利用累加法便有an－1>161n－1n≥2，所以an>16n+56>56n≥2，又a1=1>56，因此an>56n∈N.

3.试题推广

通过上述探究发现数列lnn！－n+12·lnn+n关于n单调递减且有下界，根据单调有界数列其极限必存在这一原理，我们得到以下结论：

结论  limn→+∞lnn！－n+12lnn+n=12ln2π且12ln2π

證明：由上述证明得到数列an关于n单调递减且an>56，由“单调有界原理”我们得到数列an的极限值存在.由著名的Stirling公式limn→+∞n！·ennn·n=2π可以得到 ln2π=limn→+∞lnn！·ennn·n=limn→+∞lnn！·en－lnnn·n=limn→+∞lnn！+n－n+12lnn，即limn→+∞lnn！－n+12lnn+n=12ln2π≈0.9189.由数列an关于n单调递减且limn→+∞an=12ln2π，再由数列极限的保不等式性可以得到12ln2π

综上所述limn→+∞lnn！－n+12lnn+n=12ln2π，且12ln2π