不同覆冰形态下风力机叶片翼型气动特性分析

徐琛苑 汤斯琦

DOI：10.20145/j.32.1894.20240205

作者简介：徐琛苑（1996—），女，硕士研究生；研究方向：风力机叶片气动特性，新能源电力系统规划。xuchenyuan_grid@163.com

摘要：低温环境下风力机叶片常面临覆冰的危险，研究覆冰对翼型气动特性的影响对覆冰叶片气动特性分析具有重要意义。文章采用基于有限体积法的数值模拟算法对S809二维翼型气动特性及覆冰影响进行了模拟分析。通过对比分析明冰与霜冰两种覆冰形态对翼型气动特性的影响程度，发现霜冰对翼型气动特性影响不大，而明冰则会严重恶化翼型的气动特性，甚至可能导致负阻力。

关键词：风力机叶片；气动特性；覆冰影响；数值模拟

中图分类号： TK89  文献标志码：  A

0  引言

随着全球变暖，极端气候发生越来越频繁，风力机冰冻灾害问题也越来越突出。叶片表面覆冰是风力机冰冻灾害最为突出的问题之一。叶片表面覆冰不仅给叶片增加了一个附加重力，还会改变叶片的几何外形，从而影响其气动特性［1-3］。对于MW级大型风力机超长柔性叶片，该问题尤为突出。叶片覆冰机理十分复杂，不仅与温度、湿度、风速及风向变化等周围环境有关，还与风力机叶片本身气动特性及其工作状态有关，目前尚无原型风力机三维叶片覆冰形成机理的理论解释，二维翼型覆冰形成机制也在研究中。

根据叶片表面覆冰的几何形状，可以将叶片覆冰形态分为两类：明冰［4-5］和霜冰［6-7］。当叶片周围温度低且湿度不是很高时，大气中的小尺寸液滴在与叶片表面碰撞的过程中，瞬间冻结，形成不透明霜状，此时的覆冰形态称为霜冰［6-7］。霜冰形成过程中，液滴与叶片碰撞冻结时间极短，液滴碰撞冻结位置主要受叶片周围流场及叶片表面边界层流动影响，使得覆冰形态与叶片几何外形类似，对叶片气动特性影响并不是很大。当环境温度相对较高但低于冰点，且湿度很高时，大气中液滴的尺寸较大，大尺寸液滴与结构碰撞后冻结形成的透明冰型称为明冰［4-5］。因为温度不是很低且液滴尺寸较大，液滴与结构发生碰撞后并不能马上完全冻结，只有一部分在碰撞处发生冻结，而另外一部分则沿着结构表面发生流动逐渐冻结，其在叶片表面的流动不仅与叶片表面边界层流动有关，还与叶片运动状态，如转速、桨距角、方位角等有关，这导致明冰的几何外形非常复杂且很难预测，通常会在液滴撞击点附近形成一些尖角。明冰通常具有非流线型气动外形，它将严重恶化结构的气动特性，导致大幅度的流动分离从而使阻力大幅增加，升力大幅减小。

为了准确模拟覆冰对叶片气动特性的影响，需要准确获得叶片表面的压力分布。一种方法是采用大涡模拟方法或者直接数值模拟方法，对叶片表面边界层流动进行准确解析，但解析边界层流动需要大量网格，计算成本过高。另一种方法则是采用湍流模型结合壁面函数的方法对边界层流动进行模化。不同的湍流模型对应于不同的壁面函数，例如k-ε 湍流模型通常和标准壁面函数结合使用，增强型壁面函数则通常和k-ω 湍流模型结合使用。采用何种湍流模型与壁面函数则需要一定的经验。例如，文献［8］通过S809二维翼型的数值模拟发现，精确的预测转捩分离点的位置是准确模拟翼型压力分布曲线的关键。文献［9］认为，湍流边界层对过渡区非常敏感，针对涡粘模型对边界层流动分离预测通常有所提前的弊端，提出了一种人工减小过渡区涡粘性的方法来延缓分离的发生，但该方法需要人为设定部分参数，且不同工况下参数并不相同，参数设定需要一定的经验。

风力机叶片一般都是通过一系列翼型扭转堆叠而成，研究二维翼型的气动特性对三维叶片的气动研究具有重要意义。此外，叶素理论［10］、制动线［11］、制动面［12］等叶片气动特性计算方法都是基于二维翼型气动特性附加一些修正所建立的，因此，研究二維翼型气动特性覆冰影响分析具有重要意义。本文选取S809翼型为研究对象，首先通过对比不同的湍流模型与边界层处理方法的模拟效果，验证数值模拟算法并确定最优湍流模型与边界层处理方法，进一步分析翼型表面不同覆冰形态对翼型气动特性的影响规律。

1  数值模拟参数

新能源科技

新能源科技

1.1  几何模型

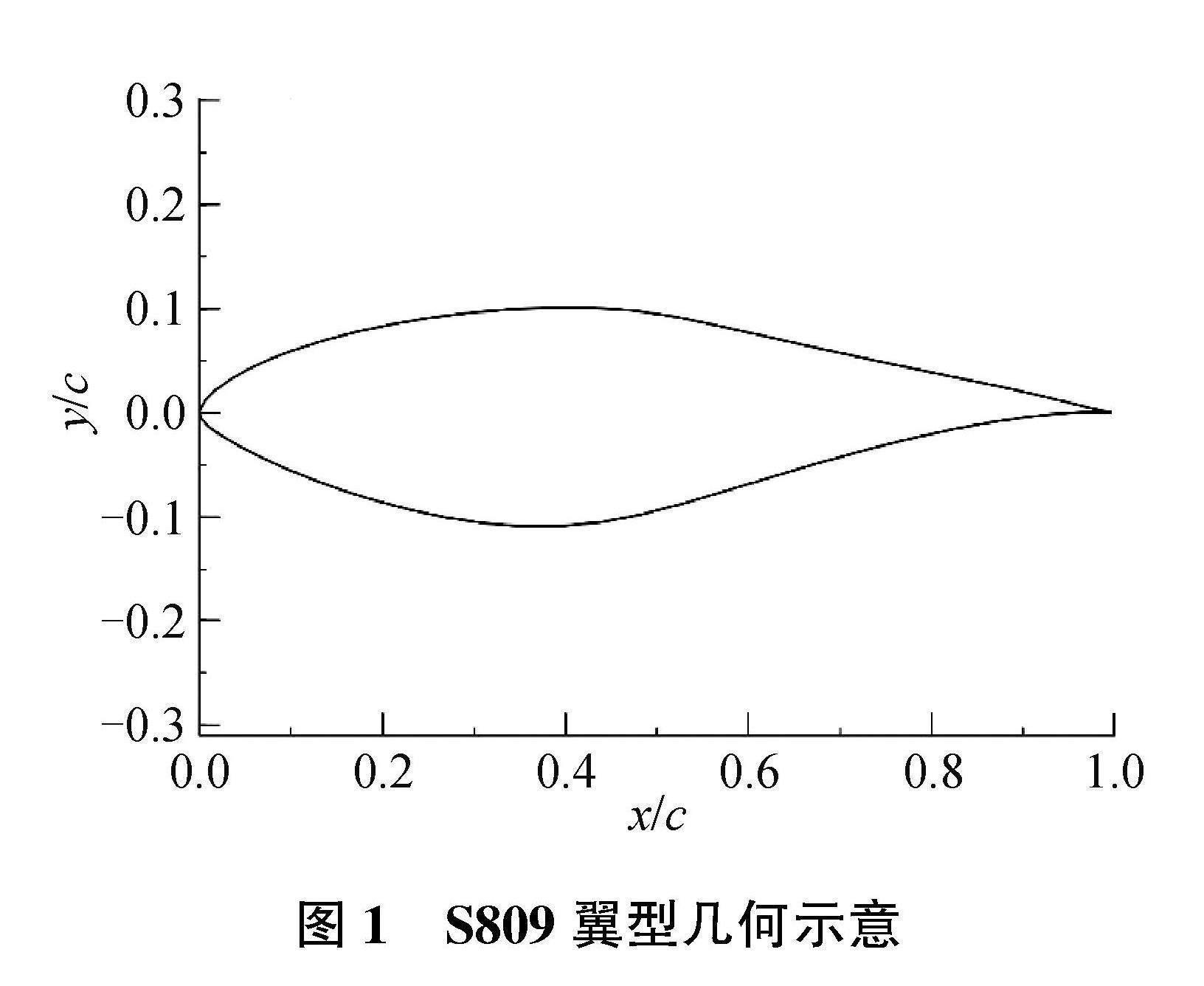
本研究选用经典翼型——S809翼型作为研究对象，其几何外形如图1所示。模拟时取弦长为

C=600mm，计算域设置为矩形计算域，翼型前缘距离入口设为

10C，距离出口为20C，翼型中心线距离计算域上下边界都为5C。边界条件设置为速度入口、压力出口，上下边界为周期性边界条件。来流选为均匀层流来流，来流速度设为U=51.7m/s，对应的雷诺数为Re=UC/ν=2×106，其中运动粘度

ν=1.55×10-6 m2/s。分别计算翼型在来流风攻角（Angle of attack，AOA）为0°、1.02°、5.13°、9.22°、14.24°和20.15°时的气动特性。

1.2  网格划分

采用C形拓扑结构的结构化网格划分方案进行网格划分。为了模化边界层流动，边界层网格划分需要满足一定要求，且对于不同的壁面模型，边界层网格划分要求并不相同，即第一层网格的高度与边界层内网格节点的数量需要满足一定要求。边界层网格划分时需要保证边界层内有足够数量的网格节点以模拟边界层的发展，一般需要在边界层内至少布置15个网格节点。根据壁面定律，第一层网格的位置可以通过其与边界层流动的关系来估算：

y1=y+νuτ（1）

式（1）中y1为第一层网格高度。uτ为摩擦速度，其与壁面剪切应力有关。在计算前并没有壁面剪切应力信息，因此，需要采用经验公式对其进行估算，经验公式为：

uτ=0.5CfU2（2）

式（2）中Cf为摩擦系数，根据F.M.White算法，Cf=0.026/Re1/7。

对于不同的湍流模型及壁面模型，边界层网格第一层网格高度不同，即y+取值不同。采用高雷诺数湍流模型时，结合标准壁面函数，要求第一层网格节点布置在湍流充分发展区，即要求y+≥30；采用低雷诺数湍流模型时，结合增强壁面函数，要求第一层网格节点布置在层流底层，即要求

y+≤5。针对本文模拟工况，当取y+=30时，由式（2）计算可得第一层网格高度

y1=0.2mm；当取

y+=5，由式（2）计算可得第一层网格高度

y1=0.03mm。需要注意的是，这里计算所得的第一层网格高度是根据经验公式估算所得，可能并不满足假设条件，一般需要根据模拟所得

y+的真实值进行调整，可以说，第一层网格高度的确定是一个重复调整的过程。来流风攻角为5.13°时的整体网格划分结果及局部网格示意如图2所示。

2  数值验证

通过对非覆冰状态下的S809翼型进行模拟分析，验证数值模拟方案的可靠性，并确定最优的湍流模型及壁面函数组合。

2.1  湍流模型对比分析

根据前人实验结果可知，S809翼型在攻角为14.24°和20.15°时处于失速区，边界层流动涉及转捩及流动分离，此时边界层流动状态的数值模拟对湍流模型、壁面函数的选择及网格的划分最为敏感。因此，通过模拟翼型在来流风攻角为14.24°和20.15°时的气动特性与流场特征，可以最为可靠的对比不同湍流模型与壁面模型组合及网格划分对模拟结果的影响。本研究共对比了Realize k-ε 湍流模型（以下简称“RKE湍流模型”）、SST

k-ω湍流模型和Spalart-Allmaras湍流模型（以下简称“S-A湍流模型”）3种湍流模型。其中RKE湍流模型为高雷诺数模型，可采用标准壁面函数，y+取值为

y+=30；SST k-ω 湍流模型为低雷诺数模型，

y+可取值为

y+=5；S-A湍流模型可采用增强壁面函数，

y+取值为

y+=5。

通过模拟所得y1值对网格进行验证。经过反复模拟与调整发现，当第一层网格高度取值为

y1=0.6mm时，对应的第一层网格无量纲高度

y+=30；而当第一层网格的无量纲高度为

y+=5时，第一层网格厚度取值应为

y1=0.09mm。

y1=0.09mm时翼型上下表面不同位置处模拟计算所得

y+的结果如图3所示，可以看出此时的

y1取值满足要求。

通常采用无量纲化的翼型表面压力系数分布曲线来描述翼型的气动特性。翼型表面压力系数计算公式如下：

Cp=P-P∞0.5ρU2（3）

式（3）中P为翼型表面压力，P∞为环境压力，U为来流风速，ρ为大气密度。

.

不同湍流模型模拟所得翼型压力系数曲线与实验结果的对比图如图4所示。从图4中可以看出，在来流风攻角为14.24°时，3种湍流模型模拟所得的压力系数分布曲线与实验所得压力系数分布曲线都符合的很好；而在来流风攻角为20.15°时，RKE湍流模型模拟结果与实验结果符合最好，SST k-ω 湍流模型模拟所得压力曲线在翼型前缘上侧有所偏低，即对边界层分离预测有所提前，而S-A湍流模型模型模拟所得压力曲线在翼型前缘上侧有所偏大，在翼型前缘下侧则有所偏低，即对边界层分离的预测有所延迟。综上所述，RKE湍流模型在3种湍流模型中对分离点的预测效果最好。不同湍流模型对边界层分离的预测也可以从速度流场云图中看出，如图5所示。

注：左侧图攻角为14.24°，右侧图攻角为20.15°

綜合上述分析可得：在较小攻角情况下，3种湍流模型对翼型气动特性模拟结果都很准确；但在攻角较大时，RKE湍流模型相对于SST k-ω 湍流模型和S-A湍流模型对翼型的气动特性模拟相对更为

准确。

2.2  数值模拟结果验证

通过对比实验与模拟所得的不同攻角下S809翼型的升阻力系数，对本文数值模拟方案进行验证。基于上述对比分析，其他攻角下翼型气动特性的模拟都采用RKE湍流模型进行模拟。升力系数及阻力系数计算公式如下：

CL=L0.5ρU2C（4）

CD=D0.5ρU2C（5）

式中L，D分别为翼型升力和阻力。

模拟结果与实验结果符合的很好，验证了本文所用数值方案的可靠性，如图6所示。此外，从图6中还可以看出，在来流风攻角为9.22°～20.15°时，由于翼型上侧边界层流动分离的发生，随着来流攻角的增大，翼型升力系数增长变缓，在较大攻角时，翼型升力系数减小。对于阻力系数，随着攻角的增大，阻力系数大幅增加。这与翼型进入失速区升阻力随来流攻角的变化规律一致。

3  覆冰影响分析

3.1  覆冰状态

本节对比分析明冰和霜冰两种覆冰形态对翼型气动特性的影响。基于大量叶片覆冰现场观测数据对叶片覆冰形态进行测绘并进行一定简化，确定翼型覆冰形态，其中霜冰与叶片几何外形相似，其厚度分布为类抛物线分布，如图7所示，在迎风点处覆冰厚度最大，本研究中霜冰最大厚度选取为0.05C，覆冰区域长度大致为0～0.3C；明冰覆冰形态较为复杂，如图8所示，其尖角突出长度为0.1C，覆冰区域大致为0～0.2C。

3.2  覆冰气动影响分析

覆冰状态下S809二维翼型气动特性的模拟方案与非覆冰状态下S809二维翼型气动特性的模拟方案一致，即相同的计算域、相似的网格划、同样采用RKE湍流及标准壁面函数，具体模拟参数设置此处不再赘述。

霜冰覆冰形态下，模拟所得覆冰翼型压力系数分布曲线与非覆冰狀态下实验所得压力系数分布曲线对比，如图9所示。从图9可以看出，覆冰状态下翼型上下侧压差略有减小。在来流攻角较小时（0°、1.02°和5.13°），覆冰翼型非覆冰区域（0.3C～C）的压力系数分布与非覆冰翼型相同。而在来流攻角为9.22°及14.24°时，由于覆冰的影响，在翼型上侧0.3C～0.5C区域，压力系数有所降低，在翼型上侧0.5C～C区域压力系数与非覆冰翼形一致，翼型下侧非覆冰区域则不受覆冰的影响。值得一提的是，在这两个攻角下，边界层流动分离点发生的位置也没有改变。在来流风攻角为20.15°时，非覆冰区域的压力分布系数也不受覆冰的影响，但此时流动分离点由于覆冰的存在有所提前。

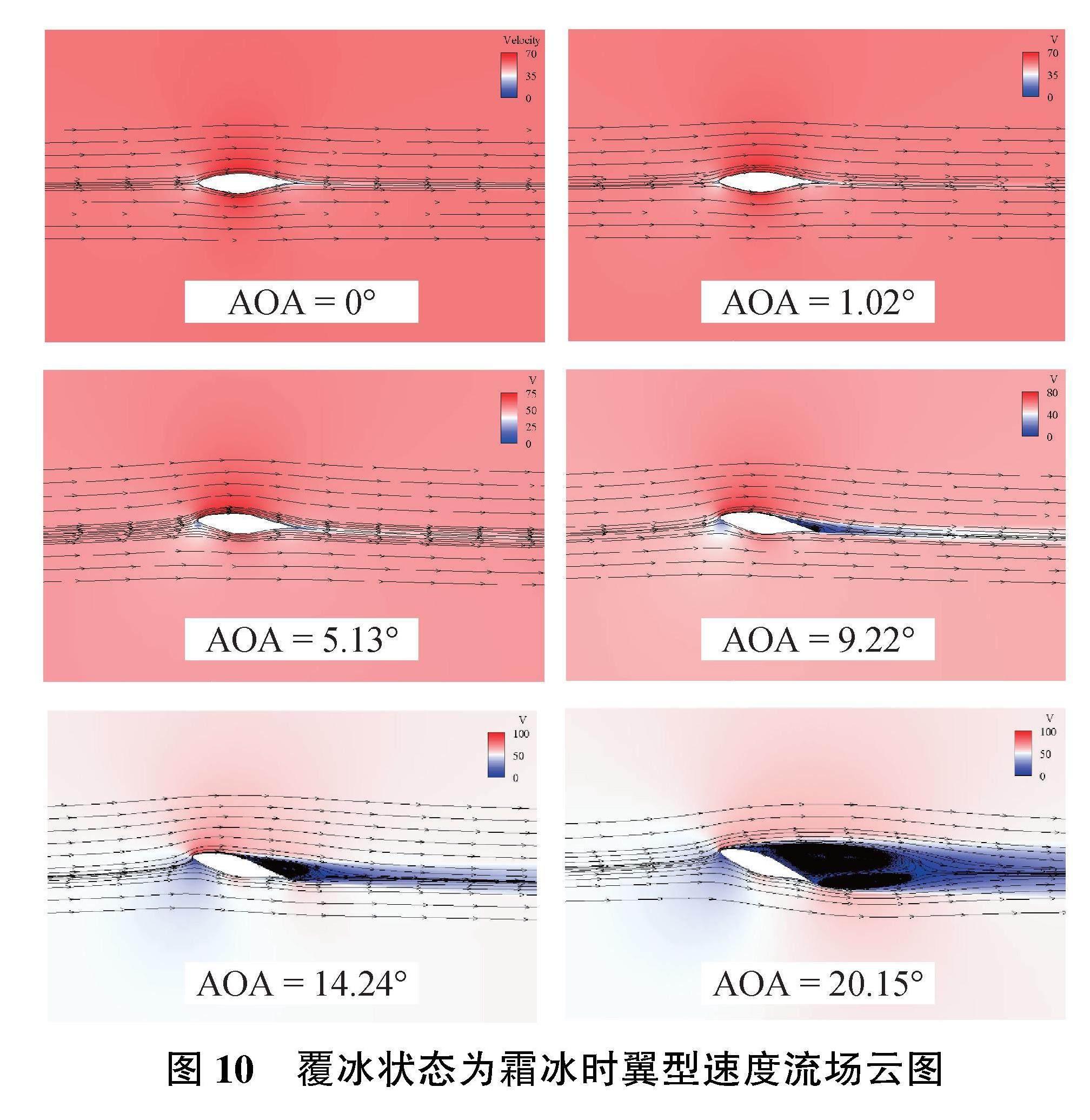
不同攻角下霜冰覆冰翼型绕流场速度云图如图10所示，可以看出，覆冰形态为霜冰时，速度流场与非覆冰翼型绕流场类似，这与霜冰覆冰翼型压力系数分布曲线结果一致。此外，霜冰覆冰翼型表面边界层流动分离点的位置也可以从速度流场云图看出。从速度流场云图所得分离点位置与通过压力系数分布曲线所得分离点位置一致，且从速度流场云图可以看出，在来流风攻角小于9.22°时，没有流动分离发生，

在来流风攻角为9.22°、14.24°及20.15°时，翼型上侧发生了稳定的流动分离，但没有漩涡脱落产生，与非覆冰翼型类似。

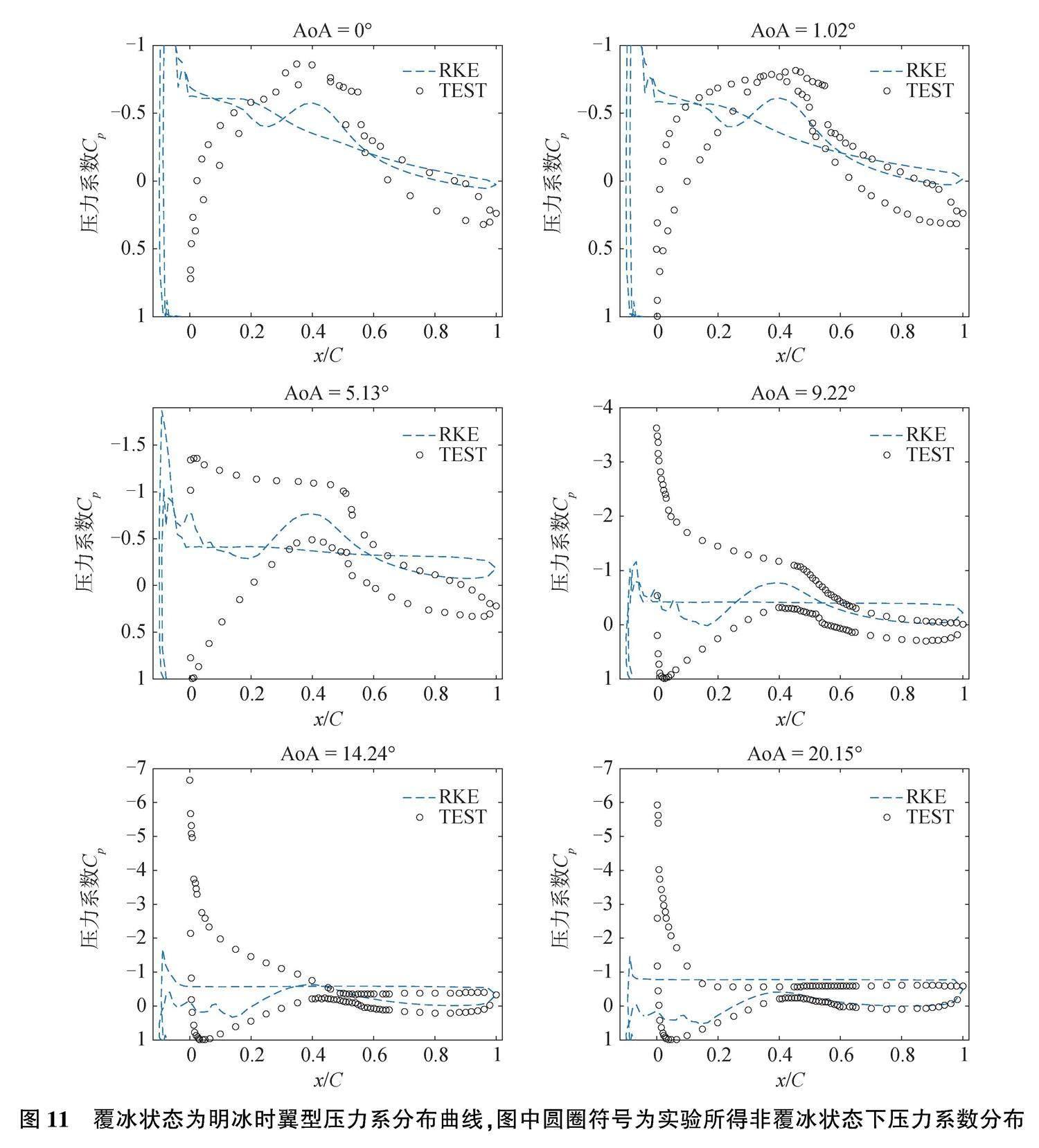
明冰覆冰形态下模拟所得翼型压力系数分布曲线与实验所得非覆冰翼型压力系数分布曲线对比，如图11所示。从图11中可以看出，由于明冰复杂几何外形的影响，翼型压力系数发生了剧烈变化，翼型上下侧压力差急剧减小，即明冰使得翼型的气动特性发生了严重的恶化。在来流风攻角

≥5.13°时，翼型上侧流动发生了完全分离。值得一提的是，在来流风攻角为20.15°时，由于非覆冰翼型分离点位于距离前缘0.2C处，非常接近迎风点，所以在翼型非覆冰区域（0.2C～C），明冰覆冰翼型压力系数分布曲线与非覆冰翼型压力系数分布曲线基本重合，而在覆冰区域（0～0.2C），明冰复杂的几何外形导致流场十分复杂，压力系数变化十分剧烈。

明冰覆冰状态下模拟所得翼型周围绕流场速度云图如图12所示。从图12中可以看出，在来流风攻角为0°和1.02°时，明冰的复杂几何外形在明冰尖角尾流区产生了两个稳定的漩涡。当来流风攻角≥5.13°时，由于来流攻角的增大，使得翼型下侧明冰尖角正对流线方向，翼型下侧明冰尖角后部漩涡消失，而翼型上侧则发生完全流动分离。

明覆冰翼型绕流场涡量云图如图13所示，从图13中可以看出，在来流攻角为14.24°和20.15°时，在尾流区产生周期性的漩涡脱落。

模拟所得明冰覆冰形态及霜冰覆冰形态下S809翼型升阻力系数随来流攻角的变化曲线如图14所示。从图14中可以看出，霜冰覆冰形态下，虽然覆冰使得翼型前缘上下侧压差有所降低，但覆冰增大了翼型的弦长，从而部分抵消了覆冰带来的影响，使得霜冰翼型升阻力系数与非覆冰翼型升阻力系数差别不大，且在来流风攻角较小时，霜冰的存在使得升力系数有所提高，在来流攻角为0°时，升力系数提高了36.24%。不同覆冰状态对翼型的升力系数与阻力系数影响程度如表1所示。同样，由于霜冰在某种意义上增加了叶片的几何长度，使得翼型表面摩擦阻力增大，从而使得霜冰覆冰状态下翼型的阻力系数有所增大。相反，对于明冰覆冰翼型，由于明冰的非流线几何外形，翼型表面边界层流动分离大大提前，流动分离也大大加剧，使得翼型的升力系数大幅减小，最大降幅达83.38%，如表1所示；且由于明冰的非流线几何外形，在大攻角下，覆冰翼型表面压差阻力大大增加，导致明冰翼型阻力系数大幅增加；值得一提的是，在来流风攻角为0°、1.02°和5.12°时，由于明冰尖角回流区的影响，覆冰的存在导致了负阻力的产生。

4  结语

本文通过S809二维翼型的数值模拟，对比分析了不同湍流模型及边界层处理方法对模拟结果的影响。通过和实验数据对比，发现

RKE湍流模型结合标准壁面函数可以很好地预测翼型表面流动的转捩与分离，得到的压力系数分布曲线与实验结果符合很好；而当流动分离较大时，SST k-ω 湍流模型对流动分离点预测有所延迟，S-A湍流模型对流动分离点预测则大幅提前。

在此基础上，本文对比分析了霜冰与明冰两种覆冰形态对翼型的气动特性的影响。主要结论如下：

（1）覆冰对翼型的气动特性的影响程度不仅与覆冰形态有关，还与来流攻角有关。

（2）霜冰对翼型的气动外形影响并不是很大，在小攻角时，霜冰对分离点几乎无影响，此时翼型升力系数有所增大；大攻角时，分离点有所提前，此时升力系数有所减小。所有攻角下，阻力系数都有所增大。

（3）明冰复杂的非流线几何外形导致流动分离的提前与加剧，严重恶化翼型的气动特性，使得翼型的升力系数大幅减小，阻力系数大幅增加。

（4）在来流攻角为0°、1.02°和5.12°时，受明冰尖角后回流区的影响，明冰的存在将导致负阻力的产生。

［参考文献］

［1］陈彦. 冷面结霜研究及风力机叶片覆冰的数值模拟［D］. 北京： 清华大学， 2012.

［2］马强，吴晓敏，陈彦. 风力机叶片覆冰的数值模拟［J］. 工程热物理学报， 2014（4）：770-773.

［3］郝艳捧，刘国特，阳林，等.风力机组叶片覆冰数值模拟及其气动载荷特性研究［J］.电工技术学报， 2015（10）：292-300.

［4］ADDY H E. Ice accretions and icing effects for modern airfoils［M］. Washington D.C.：National Aeronautics Administration， Glenn Research Center， 2000.

［5］张强，曹义华，胡利. 翼型表面明冰的数值模拟［J］. 航空动力学报， 2009（1）： 91-97.

［6］MYERS T G， CHARPIN J PF， THOMPSON C P. Slowly accreting ice due to supercooled water impacting on a cold surface［J］. Physics of Fluids， 2002（1）：240-256.

［7］杨胜华，林贵平. 霜冰生长过程的数值模拟［J］. 计算机工程与设计， 2010 （1）： 191-194.

［8］SANEI M， RAZAGHI R. Numerical investigation of three turbulence simulation models for S809 wind turbine air-foil［J］. Proceedings of the Institution of Mechanical Engineers， Part A： Journal of Power and Energy， 2018（8）：1037-1048.

［9］ROCHA P C， ROCHA H B， CARNEIRO F M， et al. A case study on the calibration of the k–ω SST （shear stress transport） turbulence model for small scale wind turbines designed with cambered and symmetrical airfoils［J］. Energy， 2016（97）：144-150.

［10］  BURTON T， JENKINS N， SHARPE D， et al. Wind Energy Handbook［M］. Chichester： Wiley， 2011.

［11］  SORENSEN J N， SHEN W Z. Numerical modeling of wind turbine wakes［J］. Journal of Fluids Engineering， 2002（2）：393-399.

［12］  YANG X， SOTIROPOULOS F. A new class of actuator surface models for wind turbines［J］. Wind Energy， 2018（5）：285-302.

（編辑  何琳）

Investigation on the aerodynamic characteristic of wind turbine blade airfoils

under different ice cover patterns

Xu  Chenyuan1，  Tang  Siqi2

（1.State Grid Jurong County Electric Power Supply Company， Zhenjiang 212400， China;

2.State Grid Zhenjiang Power Supply Company， Zhenjiang 212000， China）

Abstract：  The blades of wind turbine often face the danger of icing under low temperature environment， making it crucial to study the impact of icing on the aerodynamic characteristics of the wind turbine airfoil. This paper employs a numerical simulation based on the finite volume method to investigate the aerodynamic characteristics of the S809 airfoil and the effect of icing. Specifically， this study analyzes and compares the influence of two types of ice coverings， glaze ice and rime ice， on the aerodynamic characteristics of the airfoil. The finding reveal that the rime icing has negligible influence on the aerodynamic characteristics of the airfoil， whereas the glaze icing will significantly deteriorate the aerodynamic characteristics of the airfoil and may resulting negative drag under certain conditions.

Key words： wind turbine blade; aerodynamic characteristics; icing effects; numerical simulation