基于气象信息及风场信息的风机轮毂处风速预测

程远建+张缘

【摘 要】我国生态系统功能依然十分脆弱，环境污染迫使人类不得不开始寻求更多，更清洁的能源。风力发电是目前应用最广泛的一种新能源发电。然而由于风速的随机性会给机组、电网带来稳定性问题，因此准确地预测风速具有重要意义。鉴于目前中国风电刚起步，缺乏大量历史数据；而一般的数值模拟需要做大量的计算。本文提出一种简化的数值模拟方法。提前模拟风场的四个正方向入流、风速10m/s的标准流场，提取风机轮毂位置处数据。然后将未来一天的气象风速作为输入数据求取风机轮毂处风速。最后对研究过程中存在的误差进行了分析，并对后续基于此方法的研究提供建议。

【关键词】数值模拟 风速预测 气象信息 数据库

环境污染迫使人类不得不开始寻求更多，更清洁的能源。我国的环境形势依然极其严重，主要污染物和二氧化碳排放量都居世界第一，处于排放高平台期，生态系统功能依然十分脆弱。总体上，为了实现“十三五”环境保护规划目标，实现国民经济绿色化，深刻认识和主动适应“新常态”，提倡低碳，环保，节能。近年来，风力发电已经显示出明显的社会效益和经济效益，而且相对于其他新能源，风力发电技术更加成熟，具有大规模商业开发条件。目前风速预测主要有统计法和数值模拟，风力发电功率短期预测有利于减轻风力发电对电网的冲击，可有效地提高电网运行的安全性和经济性[1-2]。可是由于国内风电起步晚，且不断有新的风场建设，缺乏大量历史数据。因此数值模拟成为一个很好的选择。

国外研究风电场数值模拟起步较早，Astrup- Poul根据WAsP软件的线性模型对不同地面粗糙度下的复杂地形进行数值计算，对比实验结果提出了改进方法[3]。《基于CAD流场与计算的短期风俗预测方法》提出，利用fluent软件对风场进行标准入流条件模拟，提取风机出风速，建立数据库[4]。然后利用未来一天气象数据插值预测该天逐小时风机轮毂处风速。然而一般的数值模拟工程量大，计算耗时。本文基于此文章，提出一种简化算法，并结合历史数据，验证计算方法的可行性和准确性，这将在下文有所体现。

1 建模与网格划分

1.1 风场物理模型建立

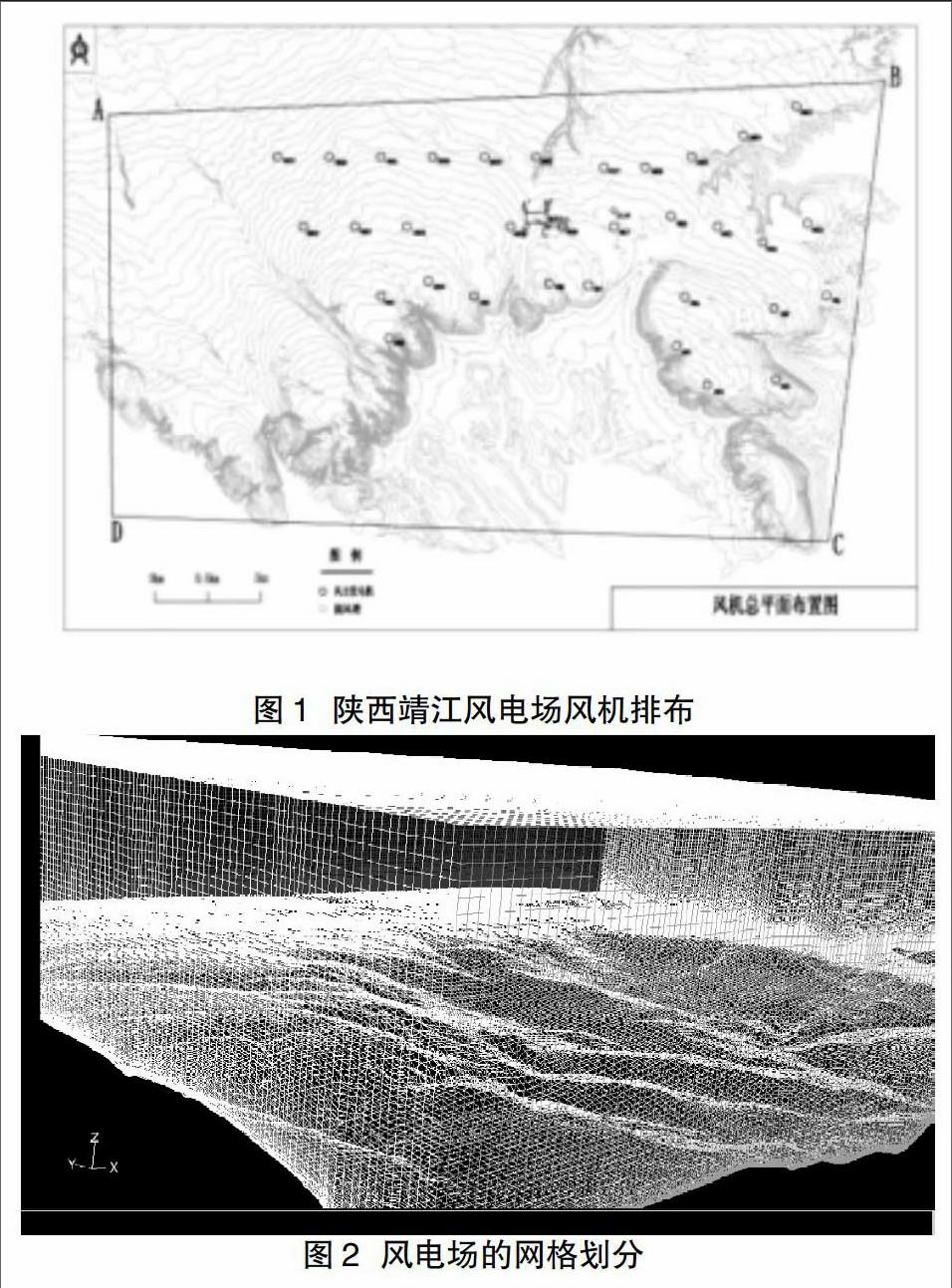
本文针对我国陕西省靖边的某个风力发电厂进行研究，靖边县位于陕西省北部偏西，靖边属于半干旱大陆性季风气候。根据当地风向玫瑰图显示：其风资源较为丰富，且盛行风向相反，以西南风和东北风为主。该风力发电厂地处山区沟壑，地势南高北低，海拔大约1123-1823m，地势起伏不太大，风场内立有一座测风塔。风机排布位置如图1。

1.2 风场内部网格划分

在计算域上进行网格划分，所建模型为5000×6000×1000（m3），考虑到风经过山体后湍流度明显加大[5]，流动更为复杂，因此背风面网格密度大于迎风面。但由于画网格十分费时且时常得不到高质量的网格，因此只在主风向上做此安排。在高度上采用网格长度递减方式划分，递减比率为0.96，总网格数329万。网格划分见图2。

2 标准入流模拟计算及数据库建立

2.1 制动盘模型

本文采用制动盘模型实现对风电场风机尾流效应的处理，设来流风速为，风轮无偏航，其中心点（轮毂处）坐标（wx，wy，wz），风轮平面某一点位置坐标为（x，y，z），则来流经制动盘的阻力源项为[6-7]：

式中Cd为制动盘的阻力系数，在0.8～1.2之间，计算中取Cd= 1.0；ρ为空气密度，Δx为制动盘的厚度。此外，在风轮平面内附加径向源项，于来流轴向源项成一定的函数关系，比例系数为η。当风向与y轴平行时，x，y，z轴上源项表达式分别为：

其中，。，，是动量守恒方程的广义源项。

2.2 入流模拟

在东、西、南、北的四个方向上进行流场模拟计算，采用k-ε迭代算法[8]。假设风向分别垂直于四个入流面，风速10m/s，切变指数0.168，模拟计算耗时6h。

2.3 建立数据库

一般的数值模拟需要建立庞大的数据库，本文提出简化改进方法，以一个简单的表格代替数据库。我们计算的是当风速为10m/s时的风场，其他入流风速时的流场可以根据10m/s成比例得出[9]。此外，我们计算了四个正方向的风入流，其他任意方向则采取矢量合成即可，这是本文的一个创新思想。具体算法如下：

设Vf为由气象预报所得的风速大小，Vfτ，Vfn为Vf的两个正交分量，则由速度三角形有：

设Vp为某风机的风速预测值，Vp的两个垂直分量为Vpτ和Vpn。且Vpτ为与Vfτ方向相同的风速预测值，U1为某风机同方向模拟计算值；Vpn为与Vfn方向相同的风速预测值，U2为某风机同方向模拟计算值；则有以下关系：

3 实际气象数据差值预测及验证修订

3.1 实际气象数据差值预测

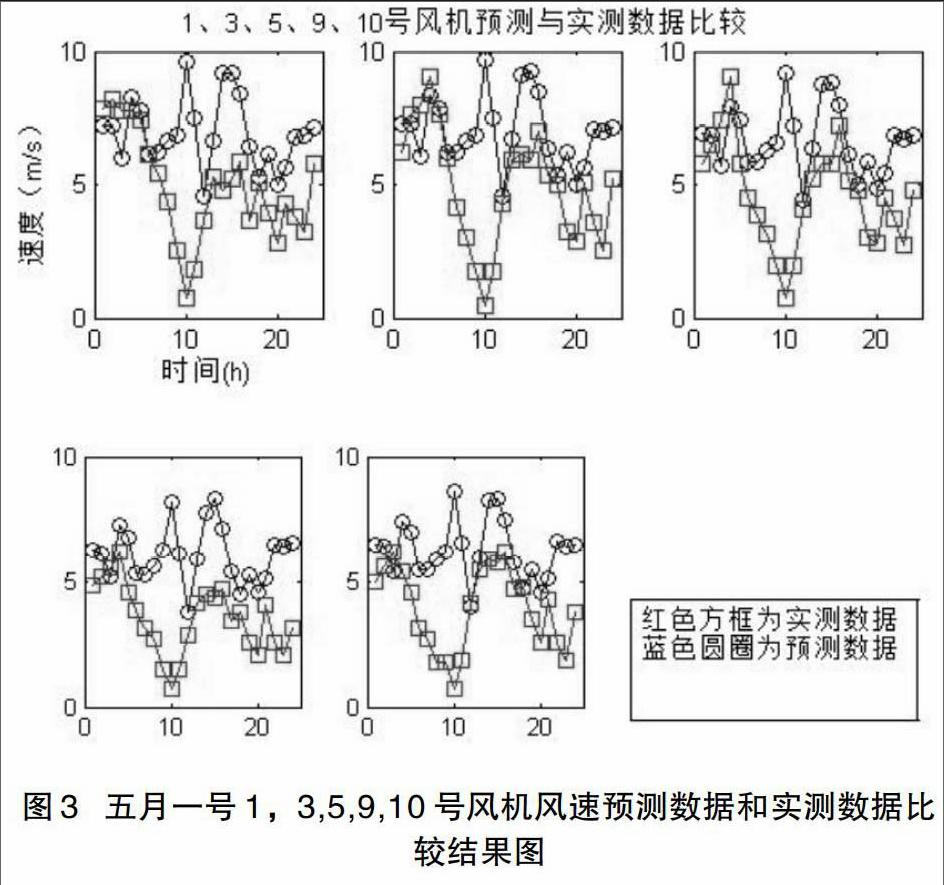
五月一号的结果分析：

有数据分析结果图可知（见图3），五月一号这一天的气象预测误差过大，平均误差为51.04%，平均值（将实测数据和预测数据先分别求取平均值在计算误差）误差为31.04%。两个值都大于要求误差范围20%。

五月二号的结果分析：

对于实验测得的数据（见图4），进行求取平均值，结果为：平均误差为26.67%，平均值（将实测数据和预测数据先分别求取平均值在计算误差）误差为11.73%。虽然平均值误差在要求误差范围20%内，但是求出的平均误差大于20%。

根据以上分析得出有以下可能的原因。

根据以上分析结果得出以下结论：

（1）一天中气温有变化，这会对风速有影响，而模拟计算时未将温度变化的因素考虑在内（即假设环境恒温）。（2）模拟划分四个正方向的流场，风速全部由10m/s推算计算得出，流场的划分和模拟计算粗略。（3）预测的最大误差来源是NWP[1]（数值天气预报）数据的误差。由于NWP数据是本预测模型唯一的输入数据，而且采用基于物理流场的风速预测原理，导致风速预测的结果对NWP数据本身的误差十分敏感。当NWP数据误差较大时，风速预测误差必然较大。（4）对于不适合发电的风速，由于风电场工作人员的人为操作，而使得测算结果不具备参考价值。

3.2 误差分析

对于减小误差，可以采取以下办法。

（1）引入气温修正系数，利用一天该风场环境气温变化数据，对预测结果进行修正。（2）实际计算可采用此方法时，可以划分八个流场，从正北风向每45°划分一个，并计算当风速分别为3m/s，9m/s，15m/s（这里仅是举例说明，风速还需根据风场的具体情况而定）。流场的轮毂出风场情况，其他风速情况采用差值法求得。（3）应提高 NWP输入数据的精度[1]，另一方面可结合对NWP数据容错性较好的统计模型方法，预测模型方面研究降低对NWP数据敏感度的方法。

4 结语

通过本文的风电场轮毂处风速的预测与分析，得到的结论有：

对于第一天风速小于启动风速3m/s的情况，其误差虽然过大，但是由于实际中此时风机处于停机状态，属于人为因素，因此不需要考虑此误差。

通过CFD数值模拟结果与实测风速比较，所得的平均误差在规定误差范围在20%以外，可以认为误差很大程度上是由于计算粗糙和来自NWP数据的误差，因此如果引入温度修正，流场划更加细致，多计算几个流速值情况，可以认为CFD计算方法对风能计算或者风功率预测有效。

对于后续基于此方法研究的建议是，不仅要考虑温度变化对风速的影响，也要更加精细划分流场，并降低预测对NWP数据的敏感度，以减小误差。

参考文献：

[1]Alexiadis M，Dokopoulos P，Sahsamanoglou H，etal.Short term forecasting of wind speed and related electrical power[J].Solar Energy，1998，63（1）：61-68.

[2]杨秀媛，肖洋，陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报，2005，11（6）：1-[2].

[3]Astrup Poul，Larsen S E. WAsP engineering flow model for wind over land and sea [M].Denmark： Riso national laboratory， 1999：1-2.

[4]李莉，刘永前，杨勇平，韩爽.基于CFD流场预计算的短期风速预测方法[J].中国工程机电学报，2013.

[5]Takahash T.wind tunnel tests of effects of atmospheric stability on turbulent flow over a three—dimensional hill[J].Journal of Wind Engineering and Industrial Aerodynamics，2005，93：155—169.

[6]Amina El Kasmi， Christian Masson. An extended k-ε model for turbulent flow through horizontal-axis wind turbines. Journal of Wind Engineering and Industrial Aerodynamics. 2008， 96（1） ：103-122.

[7]王福.计算流体动力学分析：CFD软件原理与应用[M].北京：清华大学出版社，2004：120-123.

[8]许昌.基于改进制动盘和拓展k-ε湍流模型的风力机尾流数值研究[J].中国工程机电学报，2015.

[9]梁思超.基于数值模拟的复杂地形风场风资源评估方法[J].空气动力学学报，2012.6.