“参数方程”的高三数学第一轮专题复习课例

杨玉灿

摘要：“参数方程”是高中数学理科的重点内容，也是理科数学高考的考查内容之一；考试题目出现在试卷第22题（选做题），分值为10分.高考考查的知识点主要包括直线、圆和椭圆的参数方程，在第一轮复习时，要研究高考命题的难度和类型，有针对性地展开复习

关键词：参数方程；高三数学;第一轮复习;课例

1考点分析

参数方程是理科数学选修4-4的内容，主要包括：参数方程的概念、直线的参数方程、圆的参数方程、椭圆的参数方程等.同时，参数方程也是高考数学理科考查的内容，题目出现在高考试卷的第22题.笔者对新疆2018年至2022年高考数学试卷中有关“坐标系与参数方程”考查的知识点列表（表1）统计如下：

备注：①直线的参数方程；②圆的参数方程；③椭圆的参数方程；④双曲线的参数方程；⑤抛物线的参数方程.

新疆高考所用的试卷为新课标全国卷Ⅱ或全国乙卷.笔者研究了近五年的高考理科数学试卷第22题（1）（2），其中（1）考查曲线（包括直线）的参数方程，（2）考查曲线的极坐标方程.通过2018年至2022年五年的考卷，分析试卷的命题方向及其解题类型与方法，旨在为加高三第一轮复习提供帮助.

2题型总结

在高三第一轮复习这部分内容时，一方面要了解参数的几何意义，另一方面还要掌握参数方程的形式及其基本应用.笔者根据自己多年的教学经验，总结出参数方程的基本应用有如下6种类型，仅供读者参考.

2.1类型1：参数方程与普通方程的互化

例1填空（参数方程化为普通方程）：

（1）曲线C1：x=4cosθ，y=4sinθ（θ为参数）的普通方程为＿＿＿＿；

（2）曲线C2：x=t+1t，y=t－1t（t为参数）的普通方程为＿＿＿＿.

分析：本题为2020年高考第22题的改编，直接消去参数即可得普通方程.

解析：（1）曲线C1：x=4cosθ，y=4sinθ（θ为参数）方程组中的两个式子两边平方后

相加，得x2+y2=16，即曲线C1的普通方程.

（2）曲线C2：x=t+1t，y=t－1t（t为参数）中的两个式子两边平方后

相減，得x2－y2=4，即曲线C2的普通方程.

例2把下列的普通方程化为参数方程：

（1）x2+y2=9;

（2）x2a2+y2b2=1（a＞b＞0）.

解析：

（1）曲线C1：x=3cosα，y=3sinα（α为参数）.

（2）曲线C2：x=acosα，y=bsinα（a>b>0，α为参数）.

[BP（]分析：例2（1）和（2）均可以通过平方法消去参数，所得方程即为曲线的普通方程，但要注意变量x，y的取值范围.[BP）]

点评：参数方程与普通方程两种形式的互化体现了等价转化的数学思想.

2.2类型2：求直线与曲线的参数方程

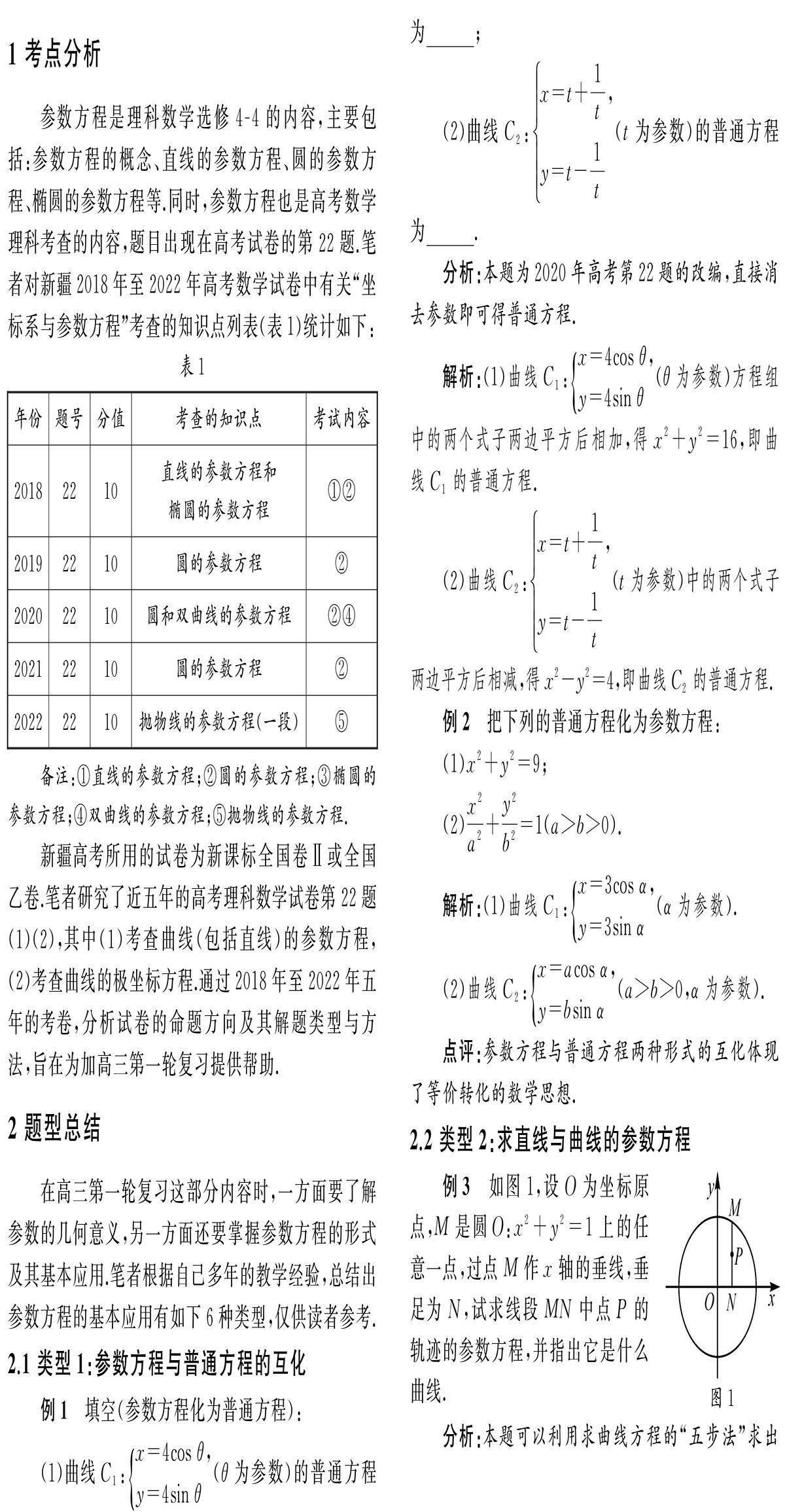
例3如图1，设O为坐标原点，M是圆O：x2+y2=1上的任意一点，过点M作x轴的垂线，垂足为N，试求线段MN中点P的轨迹的参数方程，并指出它是什么曲线.

分析：本题可以利用求曲线方程的“五步法”求出曲线的参数方程.

解析：设P（x，y），M（x0，y0），则N（x0，0）.

由点P为线段MN的中点，可得x=x0，y=y02.

因为M是圆O上的任意一点，

又圆O：x2+y2=1的参数方程为x=cosθ，y=sinθ（θ为参数），所以x0=cosθ，y0=sinθ.

所以点P的参数方程为x=cosθ，y=12sinθ（θ为参数），

普通方程为x2+4y2=1，点P的轨迹为焦点在x轴上的椭圆.

点评：本题是求曲线的参数方程，结合所给的图形，设出参数θ，建立关于参数θ的方程，体现了数形结合的数学思想.

2.3类型3：利用参数方程解决函数的最值问题

例4已知实数x，y满足（x－2）2+（y－1）2=1，试求：

（1）S=x+y的最值；（2）T=x2+y2的最值.

解析：（1）将（x－2）2+（y－1）2=1化为参数方程

x=2+cosα，y=1+sinα（α为参数，α∈［0，2π）），代入S=x+y，得

S=（2+cosα）+（1+sinα）

=3+2sinα+π4.

所以，当α=π4时，S取得最大值3+2；当α=5π4时，S取得最小值3－2.

（2）结合（1）中的参数方程，得

T=x2+y2

=（2+cosα）2+（1+sinα）2

=6+25sin（α+φ）.

由于tanφ=2，因此当sinα=55，cosα=255

时，T取得最大值6+25，当

sinα=-55，cosα=-255

时，T取得最小值6－25.

点评：本题是利用圆的参数方程，通过“三角换元”转化为三角函数的最值问题.这也是我们求最值常用的三角换元法.对于（2）也可以用“几何法”求解，式子x2+y2的几何意义是原点到圆（x-2）2+（y-1）2=1上点的距离的平方.

2.4类型4：利用参数方程解决曲线上的点到直线距离的最值问题

例5在椭圆C：x29+y24=1上求一点M，使其到直线l：x+2y－10=0的距离最短，并求出这个最短距离.

解析：利用椭圆C的参数方程可设点M的坐标为（3cosα，2sinα），则点

M到直线l的距离

d=|3cosα+4sinα－10|5=5|sinα+φ－2|.

当sinα+φ=1时，点M到直线l的距离最短.由于tanφ=34，

因此sinα=45，cosα=35时，点M95，85，最短距离为5.

点评：先把椭圆的普通方程化为参数方程，再把点M到直线l的距离转化为关于参数的三角函数的最值问题.

本题也可以采用平移相切法来处理.

本题采用三角换元法解题，体现了数学的化归思想.

2.5类型5：利用参数方程解决弦长问题

例6求直线C1：x=1+tcos60°，y=tsin60°（t为参数）被圆C2：x2+y2=1所截得的弦长.

解析：将直线C1：x=1+tcos60°，y=tsin60°（t为参数）代入x2+y2=1，整理，得

t2+t=0，解得t1=0，t2=－1.

所以，截得的弦长为|t2－t1|=1.

点评：根据参数t的几何意义，|t|为直线上的点到点（1，0）的距离，可知|t2－t1|为直线被圆截得的弦长.

2.6类型6：曲线（包括直线）的参数方程的综合性应用问题

例7已知曲线C的参数方程为x=1+2t，y=at2（其中t为参数，a∈R），点M（5，4）在曲线C上.

（1）求常数a的值；（2）写出曲线C的普通方程.

解析：（1）曲线C的参数方程x=1+2t，y=at2（t为参数）可化为普通方程4y=a（x－1）2.

由点M（5，4）在曲线C上，得

4×4=a（5－1）2，即a=1.

（2）由（1）知，曲线C的普通方程为（x－1）2=4y.

例8已知直线C1：x=1+tcosα，y=tsinα（t为参数），圆C2：x=cosθ，y=sinθ（θ为参数）.

（1）当α=π3时，求C1与C2的交点的直角坐标；

（2）过原点O作直线C1的垂线，垂足为A，P为OA的中点，当角α发生变化时，试求动点P的轨迹.

解析：（1）当α=π3时，可得直线C1的普通方程y=3（x－1）.圆C2：x=cosθ，y=sinθ（θ为参数）的普通方程为x2+y2=1.

由x2+y2=1，y=3（x-1），解得x1=12，y1=－32，或x2=1，y2=0.所以C1与C2的交点坐标为12，－32和（1，0）.

（2）因为C1的普通方程为

xsinα－ycosα－sinα=0，①

所以过坐标原点且垂直于C1的直线方程为

xcosα+ysinα=0.②

联立①②，可得A（sin2α，－sinαcosα）.

当角α发生变化时，点P的轨迹的参数方程为

x=12sin2α，y=－12sinαcosα（α为参數）.

消去参数α，可得点P的轨迹的普通方程

x－142+y2=116.

故点P的轨迹是圆心为14，0，半径为14的圆.

点评：本题考查了直线与圆的参数方程以及直线与圆的位置关系.

3结束语

本课例列举了参数方程的六种题型，通过本节课的教学，帮助学生厘清参数方程的题型特征与解题方法，学会分析与思考解参数方程相关问题的通性与通法.本文中根据近五年高考第22题列表统计与分析，帮助老师和学生了解高考有关参数方程命题的方向，另外，通过对这些题型的探究与解析，帮助学生学会分析其他数学难题，拓展参数方程的应用范围.由于“参数方程”在高考数学中特殊而重要的地位，因此在第一轮复习时，要研究高考命题的难度和类型，从而有针对性地进行第一轮复习，且要注意复习的实效性，切实让学生弄懂学会，在应对高考或“模考”时，信心满满，游刃有余！并在此过程中培养学生的数学运算与逻辑推理等核心数学素养.