利用GGB软件辅助高中数学新教材函数教学

李梅 蔡华

摘要： 函数是数学中一个重要的概念，也是新教材高中数学教学的重点和难点.如果教师能巧妙地利用函数图象将抽象的问题转化为直观的图形，则可以帮助学生有效地理解函数，也可以大大降低学习函数的难度.利用GGB软件展示一些常见的函数图象，让学生充分进行观察和思考，并总结出相关函数的图形的特征.这样就可以有效辅助函数的教学工作，从而相对轻松地突破高中阶段的重点教学内容.

关键词： 函数；GGB软件；辅助函数教学；数形结合

函数是数学中一个重要的概念，也是高中数学教学的重点和难点.图象是描述函数变量之间关系的途径之一，中学阶段要研究的函数主要有

一次函数、二次函数、指数函数、对数函数、三角函数和幂函数等.如果学生不清楚这些函数的图象，或者不明确影响函数图象的因素，就很难真正掌握这些函数，更不用说利用相关的函数性质来解决实际问题了.如果教师能巧妙地利用函数图象将抽象问题转化为直观的图形，则可以帮助学生有效地理解函数，也可以大大降低学习函数的难度.近年来，GGB软件是一种操作简单方便且形象直观、功能强大的数学作图软件，使用范围非常广泛.我们可以充分利用GGB软件展示一些常见的函数图象，让学生充分进行观察和思考，并总结出相关函数的图象特征.这样就可以有效地辅助函数的教学.

本文中将从人教A版（2019）高中数学必修第一册中三类函数的教学入手，例谈如何有效利用GGB软件辅助高中数学中的函数教学.

1 实例一：指数函数底数对函数图象的影响

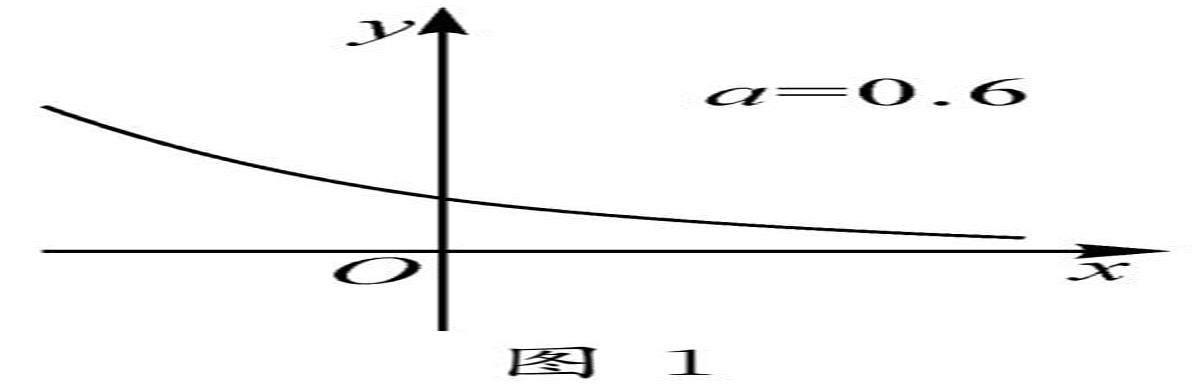
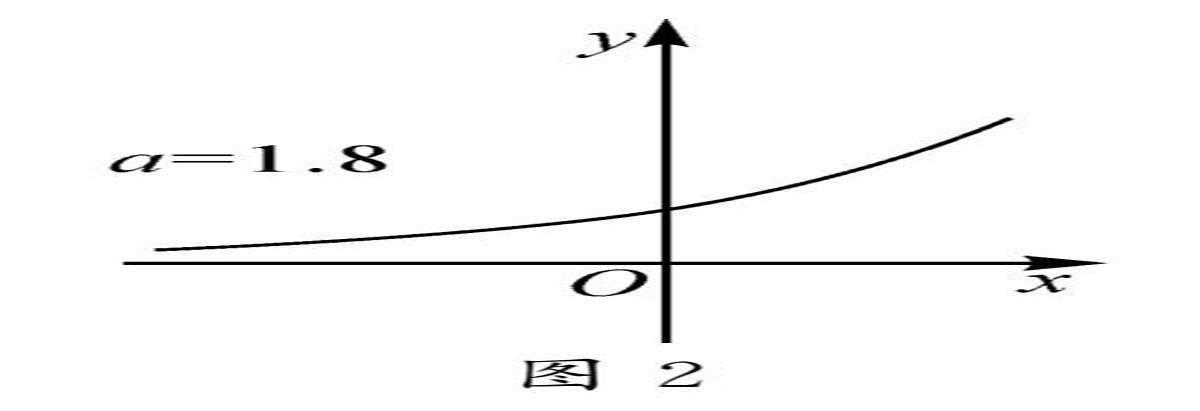
在指数函数y=ax（a>0且a≠1）的教学过程中，若想研究底数a对函数图象的影响，在利用GGB软件画图时，可以用滑动条控制参数a，通过拖动滑动条，仔细观察a对图象产生的影响，然后进行总结.学生通过观察发现：当底数01时，指数函数y=ax的图象呈现上升趋势，随着x的不断增大，y值也在不断增大，图象呈现出“一撇”状（如图2）.

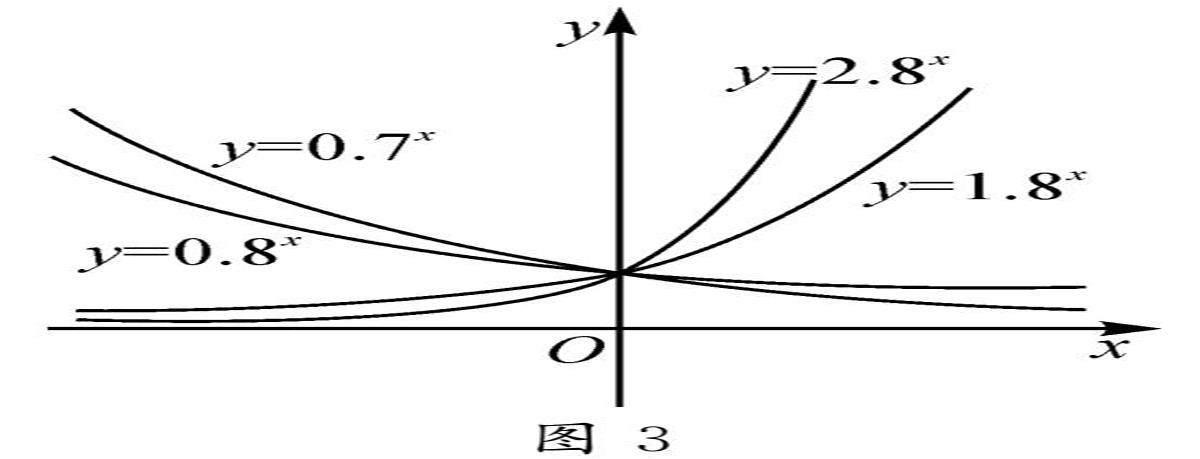
为了进一步研究底数的变化对图象的影响，可以利用GGB软件在同一个直角坐标系中画出四个指数函数y=2.8x，y=1.8x，y=0.7x，y=0.8x的图象（图3）.还可以拖动滑动条，让底数a不断变化，通过观察我们发现在y轴右侧区域，底数越大图象越高，顺理成章也就总结出了指数函数图象在y轴右侧区域“底大图高”这一规律.这样形象直观，也大大降低了学生学习指数函数的难度.

如果不使用信息技术，只能手工列表描点作出有限的几个人为设定的特殊函数的图象，然后观察这几个图象来讨论指数函数的性质，显然会带来一些问题，比如，为什么要画这几个函数的图象？为什么几个具体的函数图象就可以代表一般的函數图象？由此得到的性质是否可靠？利用GGB软件，作图更加方便，学生也能通过大量的函数图象看到共性，更容易概括出指数函数的性质.

2 实例二：双曲函数的相关性质

在学习拓展内容——函数f（x）=x+ a x 时，可以利用GGB软件画出相应的函数图象，然后观察函数的图象，就可以轻松看出函数的单调性、奇偶性、最值、渐近线等一系列的相关性质.

在画图时可以用滑动条控制参数a.通过拖动滑动条观察a对图象产生的影响.我们发现：当参数a>0时，图象（图4）呈现出对勾形；当参数a<0时，图象（图5）不再呈现对勾形；当参数a=0时，函数的图象（图6）为过原点的一条直线.

通过观察，发现图4和图5中的曲线都有相同的渐近线y=x.当参数a>0时，函数f（x）=x+ a x 在区间（－∞，－ a ），（0， a ）上单调递减，在区间（－ a ，0），（ a ，+∞）上单调递增；当参数a<0时，函数f（x）=x+ a x 在区间（－∞，0），（0，+∞）上均单调递增.不论参数a取何值，函数的图象均关于原点对称，函数f（x）=x+ a x 为奇函数.

所以利用GGB软件可以轻松作出双曲函数的图象，通过对精准函数图象的观察，学生很容易了解函数的相关性质，形象且直观，这样就大大降低了学生学习函数的难度.

3 实例三：三角函数各参数对其图象的影响

在学习三角函数y=Asin（ωx+φ）的图象时，学生很难感受到每一个参数对于函数图象的影响.如果能巧妙灵活使用GGB软件，把其中的参数A，ω，φ均用参数按钮设置成对应的变化框或者滑动按钮，展示图象的变化过程，学生就可以清晰、直观地感受到每个参数对图象的影响.

（1）研究参数A对函数图象的影响

可以输入不同的A（A＞0）值，让学生观察总结出A对函数的最值是有影响的，对周期、单调性均不产生影响，如图7.

（2）研究参数ω对函数图象的影响

通过改变变量ω（ω＞0）的值，引导学生观察总结出ω影响的是函数的周期，如图8.当ω=2时，图象上所有点的横坐标缩短为原来的 1 2 ;当ω= 1 2 时，图象上所有点的横坐标伸长为原来的2倍.

（3）研究参数φ对函数图象的影响

通过改变变量φ的值，引导学生观察总结出φ影响的是函数的位置，如图9.当φ>0时，图象上所有点向左移动;当φ<0时，图象上所有点向右移动.

通过GGB软件作图，我们可以准确地展示图象的变换，让学生能够直观地感受到每个参数对图象的影响，可以很好地帮助学生理解这类函数的相关性质.

函数是高中数学的核心内容，也是培养学生分析问题和解决问题能力的重要内容.“数形结合”法能够使抽象的数学问题具体化，将数学的研究方法和解题策略具体化，能让学生在学习中更好地理解知识、掌握方法.而实现数形结合的有力工具就是精准的GGB作图软件，所以我们要合理、有效、有意识地使用这种软件来助力教学.高中函数教学要基于教材和学生实际，结合学生的数学学习情况，探索更合适的教学策略，帮助学生掌握更好的学习方法.当然，在教学过程中不能仅关注知识和技能的传授，还应该培养学生的核心素养.这就需要教师注重培养学生的数学思维和解决问题的能力.数形结合法可以让学生更好地掌握函数知识，形成数学思维和解决问题的能力，从而提高高中函数教学水平.