笛莎格定理
顾森
吉拉德·笛沙格是17世纪法国著名的工程师和数学家,在工程方面,他设计了巴黎和里昂的多幢建筑,还为塞纳河制作了一套抽水系统,在数学方面,他发现了很多漂亮的几何规律,奠定了射影几何这一数学分支的基础.下面这个神奇的规律就是笛沙格发现的.
过点O作三条直线.在第一条直线上任选两个点,记作A,A;在第二条直线上任选两个点,记作B,B';在第三条直线上任选两个点,记作C,C'.我们得到了△ABC和△A'B'C'.作直线BC和B'C',两者交点记为X;作直线AC和A'C',两者交点记为Y;作直线AB和A'B',两者交点记为Z那么,X,Y,Z三点一定在一条直线上.
这个规律真的对吗?你可以用直尺和铅笔,在草稿纸上作图试试.不过,画完图之后,你或许会有疑问:纸上画出的X,Y,Z三点看起来好像是在一条直线上,但这是精准的吗?学过了一次函数之后,我们有一个更好的方法来验证这个规律,在平面直角坐标系里,几何元素的各种属性都能用数字确切地刻画出来,点X,Y,Z的位置也能毫无误差地计算出来.这样,我们就能精准地验证这个规律了.
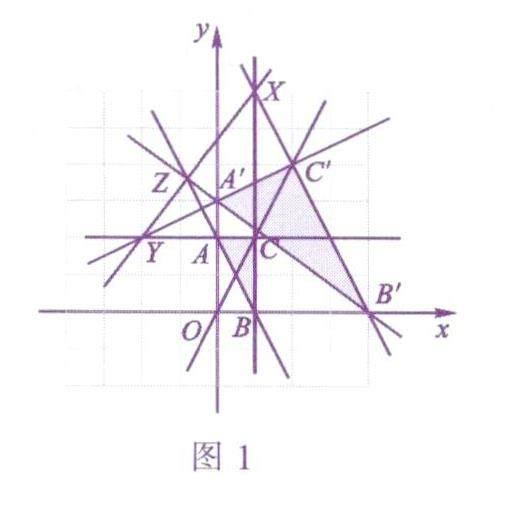
如图1,不妨假设点O是坐标原点(0,0),過点O的三条直线依次是x轴,y轴和直线y=2x.假设点A和A'的坐标分别为(0,2),(0,3),点B和B'的坐标分别为(1,0),(4,0),点C和C'的坐标分别为(1,2),(2,4).为了求出这些点确定的直线,我们可以使用待定系数法.直线BC就是一条过点(1,0)且平行于y轴的直线,直线B'C'的解析式是y=-2x+8.代入x=1,得到y=6.因此,点X的坐标就是(1,6).直线AC就是一条过点(0,2)的水平线,直线A'C'的解析式是y=1/2x+3.代入y=2,得到x=-2.因此。点Y的坐标就是(-2,2).再次利用待定系数法,可以得到直线Xy的解析式为y=4/3x+14/3.
最后,我们来求一下点Z的坐标.直线AB的解析式为y=-2x+2,直线A'B'的解析式为y=-3/4x+3.这样,我们就得到了一个二元一次方程组.解这个方程组,得到x=-4/5,y=18/5.点z的坐标就是(-4/5,18/5).这个点是否在直线XY上呢?让我们把点Z的横坐标-4/5代入直线XY的解析式,得4/3×(-4/5)+14/3=-16/15+14/3=18/2,正好等于点Z的纵坐标.这说明,X,Y,Z三点确实在一条直线上.
我们这里只是对其中一种情况进行了验证.不过,即使三条直线的解析式变了,以及点A,A',B,B',C,C'的坐标变了,利用同样的方法,我们仍然可以检验规律的正确性,事实上,我们可以直接把三条直线设为y=k1x,y=k2x,y=k3x,把点A,A',B,B',C,C'的坐标设为(x1,k1x1),(x'1,k1x'1),(x2,k2x2),(x'2,k2x'2),(x3,k3x3),(x'3,k3x'3).带着这些字母进行计算,把点X,Y,Z的坐标都表示出来,就可以验证在任何情况下点Z都会落在直线XY上.这样就证明了笛沙格发现的规律始终成立.当然,这种证明方法的代数运算量会非常庞大.但这并不是不能完成,利用计算机等工具,这个计算任务就会变得非常轻松.
正方形拉伸后会变成长方形,四边不再一样长了.正方形在透视作用下还会变成平行四边形,连内角都变了,但笛沙格发现的几何规律很有意思:条件和结论都只涉及点和直线的位置关系,完全不涉及角度关系、长度关系、面积关系.因此,将图形随意拉伸变形,甚至是改成各种透视图,条件和结论都不会发生变化——该在某条直线上的点,肯定还会在这条直线上:该过某个点的直线,肯定仍然会过这个点,这种类型的几何规律就是射影几何的研究对象.
笛沙格的发现在射影几何中非常重要,后人把它叫作“笛沙格定理”.
2023年12月号“数学潜能知识竞赛”
参考答案
1.B 2.C 3.-3/4 4.1 5.1/8 6.(1)不能.(2)10060元.
2023年12月号“数学潜能知识竞赛”获奖名单
(括号内为辅导老师)
金子耀 张珊尼(郭卫锋) 于金朋(刘晓玲) 焦梓峻(刘莎) 杨忠桦(陈星)
朱家慕 于浩轩(陈星) 韩赓(马婷) 孙人则(柴国江) 程俊杰(魏月娥)
王秉法 闫涵(魏月娥)
- 中学生数理化·八年级数学人教版的其它文章
- “一次函数的图象与性质”划重点
- 当当闯关记
- 数学潜能知识竞赛
- “一次函数”新题总动员
- “函数及其图象”夯基础
- “一次函数”易错题专练

