一次函数增减性的应用
2024-05-24 17:37于化平
中学生数理化·八年级数学人教版 2024年5期
于化平
对于一次函数y=kx+b(k≠0),当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.这就是一次函数的增减性,利用此性质可解决诸多问题.
一、求函数值
例1 已知一次函数y=kx+3的函数值y随x的增大而减小,则当x=2时,y的值不可能是( ).
A.-4 B.-l
C.2 D.4
解析:对于一次函数y=kx+3,因y随x的增大而减小,所以k<0.
当x=2时,y=2k+3<3,故选D.
二、确定字母的取值范围
例2 一次函数y=(k-3)x+2的函数值y随x的增大而减小,则k的取值范围是( ).
A.k>0 B.k<0
C.k>3 D.k<3
解析:对于一次函数y=(k-3)x+2,y随x的增大而减小,所以k-3<0,即k<3.故选D.
三、确定函数图象的位置
例3 对于一次函数y=kx-k,若y随x的增大而减小,则该函数图象经过( ).
A.第一、二、三象限
B.第一、二、四象限
C.第二、三、四象限
D.第一、三、四象限
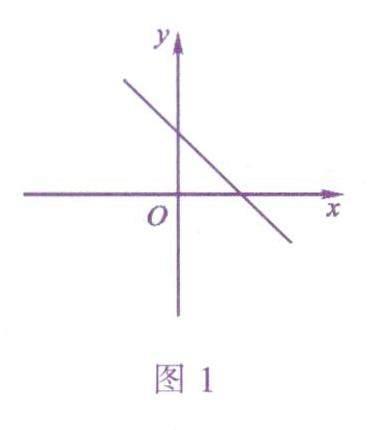
解析:由y随x的增大而减小,可得k<0.所以b=-k>0.所以一次函数y=kx-k的图象与y轴的交点在y轴的正半轴,方向是由左向右“斜向下”.画出大致图象如图1所示.所以一次函數y=kx-k的图象经过第一、二、四象限,故选B.
四、求函数解析式
例4 已知一次函数的图象过点(1,3),且y随x的增大而增大.请写出一个符合上述条件的函数解析式:________.
解新:设一次函数的解析式为y=kx+b(k≠0).
由一次函数y=kx+b的图象经过点(1,3),可得3=k+b.
又因为函数值y随x的增大而增大,所以k>0.所以可令k=1,b=2,符合题意.
因此,符合上述条件的函数解析式可以为y=x+2(答案不唯一).
猜你喜欢
新高考·高一数学(2022年3期)2022-04-28
装备制造技术(2021年4期)2021-08-05
语数外学习·高中版上旬(2020年8期)2020-09-10
语数外学习·初中版(2020年8期)2020-09-10
语数外学习·高中版上旬(2020年8期)2020-09-10
河北理科教学研究(2020年4期)2020-03-09
电镀与环保(2018年4期)2018-08-20
汽车实用技术(2015年8期)2015-12-26
今日中学生(初三版)(2013年6期)2013-07-30
金属加工(热加工)(2013年11期)2013-06-28
- 中学生数理化·八年级数学人教版的其它文章
- “一次函数的图象与性质”划重点
- 当当闯关记
- 数学潜能知识竞赛
- “一次函数”新题总动员
- “函数及其图象”夯基础
- “一次函数”易错题专练

