黔西南金矿砂岩动静组合加载岩石力学特性研究

左宇军,胡 赏,林健云,潘 超,孙文吉斌,陈 斌,陈庆港,荣 鹏

(1.贵州大学 矿业学院,贵州 贵阳 550025;2.贵州大学 资源与环境学院,贵州 贵阳 550025)

随着矿产资源长期持续的大规模开采,浅层资源日益枯竭,深部开采成为必然[1]。开采深度的增加使得高应力对巷道围岩破裂及稳定性的影响变得更为明显[2-3]。对于极难维护的高应力巷道,基于卸压技术实现应力转移比加强支护可以取得更好的巷道围岩稳定性控制效果。卸压技术具有独特的优越性[4-5]。钻孔爆破卸压是一种广泛使用的卸压技术,具有转移高应力、改善深部巷道维护状况、施工方便等优点。巷道围岩不同深度的切向应力大小不同,围岩在相同的冲击载荷下的动力学行为也理应不尽相同。为保证爆破卸压在深部高地应力巷道的应用可靠与安全,必须开展动静组合加载试验,对不同应力状态下岩石的动力学特性展开研究。

在动载岩石力学特性方面,国内外学者借助霍普金森压杆系统开展了动载下岩石力学特性、能量耗散、破坏特征研究。LI等[6]分析了不同角度和长度的预制缺陷对动态力学性能的影响。宫凤强等[7]研究发现在围压一定情况下,岩石的动态压缩强度随应变率的提高而提高;在应变率相同情况下,岩石的动态压缩强度与弹性模量随围压的增大而增大。ZHAI等[8]研究了冻融后岩石的微观损伤、宏观断裂特征和动力特性,探讨了砂岩试件的分形特性、能量演化和动态抗压强度变化规律。ZHAO等[9]发现破损砂岩的碎片粒度分布和能量耗散密度与分形维数相关。ZHAO等[10]在总结前人对裂隙岩石在动荷载作用下力学性质的试验和数值研究的基础上,重新量化了裂隙岩石样品的力学变化模式。FAN等[11]用一维分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)对深层砂岩进行动态测试,获得了不同角度和不同冲击压力下深层砂岩的分形维数、能量演化和分布曲线。金解放等[12]开展红砂岩冲击实验,研究了应变率、轴压对试样能耗特性及破坏模式的影响。ZHOU等[13]测量了循环载荷下岩石动态强度随损伤和应变速率的变化。刘少虹等[14]发现煤岩结构动载能量耗散随应力波幅值的增大而增大,随静载的增大呈现先增大后减小的趋势。左宇军等[15]基于动态岩石破裂过程分析系统RFPA2D 对大直径SHPB 装置中压杆的应力波弥散效应进行二维数值分析,分析了矩形应力脉冲和三角形应力脉冲2种加载波形对弥散结果的影响。李地元等[16]对层状黄砂岩试样施加一维动静组合载荷,发现动静组合荷载作用下,随层理倾角的增大,含孔洞层状黄砂岩试样的动态强度总体上呈现出先增大后减小的变化规律。HU等[17]研究了加卸荷损伤砂岩的动力学特性, 获取了不同卸荷损伤应力对岩石动态力学行为的影响。

本文以黔西南金矿深部高地应力巷道围岩爆破卸压问题为背景,基于改进的SHPB系统,进行动态压缩试验,研究动静组合加载条件下岩石的力学响应和能量演化规律,这对探究深部高地应力巷道切向应力影响下围岩爆破动载响应行为,确保爆破卸压技术的可靠应用具有重要意义。

1 试验设计

1.1 试样制备及物理力学参数

选用完整性和均匀性较好的岩石部分制成直径50 mm,长度25 mm的试样若干,并对端面进行打磨,使其不平行度和不垂直度均小于0.02 mm。基于静力学试验获取了岩石物理力学参数,见表1。

表1 岩石物理力学参数Tab.1 Rock physical and mechanical parameters

1.2 试验方案

巷道开挖后围岩沿径向在不同深度的切向应力有不同程度的增加,不同位置的应力状态各不相同。当进行卸压爆破时,不同应力状态的岩石受动载荷作用下的力学响应各不相同,如图1所示。

图1 巷道围岩动静组合加载作用示意图Fig.1 The schematic diagram of dynamic and static combined loading of roadway surrounding rock

基于该工程背景,设置不同的轴压进行动静组合加载试验。将试样放置于分离式霍普金森压杆上,轴压分别加载至0,10,20,30,40 MPa,加载速度为0.5 MPa/s,然后对试样进行动态压缩试验,冲击气压均为0.2 MPa。应力加载路径如图2所示。

图2 应力加载路径Fig.2 Stress loading path

1.3 试验系统

压杆直径均为50 mm,入射杆长度2 500 mm,透射杆长度2 500 mm,子弹长度400 mm,材质均为钢,密度7.9 g/cm3,弹性模量190 GPa,波速5 000 m/s。冲击气压压力范围0.1～0.7 MPa。

根据入射杆和透射杆上应变片采集到的应变信号,结合一维应力波理论,可以推导出试样的应力、应变和应变率,表达式[18]为

(1)

2 实验结果与分析

2.1 动态应力平衡关系

一维动静组合加载试验要满足应力平衡假设。以轴压40 MPa试样为代表,进行动静组合加载,试验直接采集到的入射波、透射波、反射波的原始波形如图3(a)所示。在圆柱形的子弹冲击下,入射波为矩形波,通过数据处理获取试样两端的应力随时间的变化情况,如图3(b)所示。由图3(b)可以发现入射应力与反射应力之和与透射波高度吻合,证明本文试验满足应力均匀性假设。

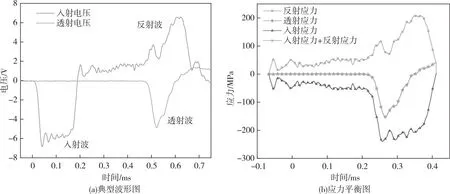
图3 应力平衡检验Fig.3 Stress balance test

2.2 应力应变

根据试验结果获得不同轴压下的砂岩动态应力-应变曲线,如图4所示。由图4可见曲线存在不同程度斜率增加的阶段:动静组合加载作用下试样产生压密阶段,试样内部微裂隙闭合。压密阶段之后是弹性阶段,该阶段满足胡克定律,应力与应变的线性关系明显,表明此阶段各条件试样均产生了不同程度的弹性响应。随着应力、应变的增加,曲线进入裂纹非稳定发展阶段,斜率逐渐减小,岩石从弹性阶段转入塑性阶段,裂纹不断发展,直到试样破坏。曲线在峰值之后进入峰后阶段,试样表现出不同程度的残余强度。子弹头为圆柱形子弹头,其产生的应力波为矩形波,这使得试样应力-应变曲线产生波动,在峰值及峰后会有多个应力、应变峰值产生。由应力-应变曲线可知,存在轴压时应力、应变的最高峰值为首峰,而无轴压时则非首峰。观察冲击后试样碎屑可以发现,试样破坏后碎屑中的大块率随着轴压的增加而逐渐减少。

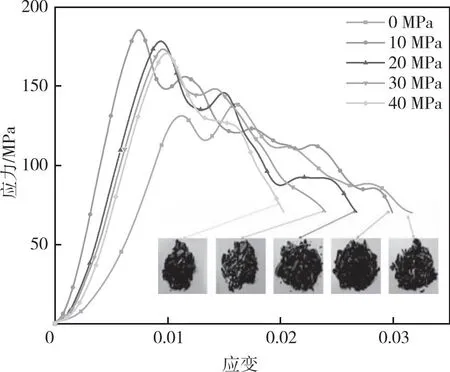
图4 砂岩动静组合加载应力应变曲线Fig.4 Sandstone dynamic and static combined loading stress-strain curves

极限应变为试样动态应力-应变曲线中的最大应变值,一定程度上代表砂岩的变形特性[19]。不同轴压下岩石的极限应变、峰值应变的变化如图5所示。对于极限应变,随着轴压的增加,极限应变逐渐降低。对于峰值应变,无轴压时最高;有轴压时,峰值应变随着轴压的增加而逐渐增加。这表明轴压的增加限制了试样最终破坏时的变形。

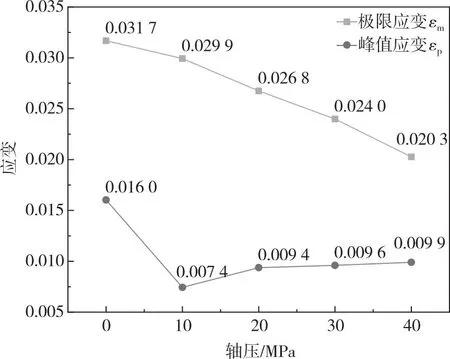
图5 极限应变、峰值应变与轴压关系Fig.5 The relationship between ultimate strain, peak strain and axial compression

2.3 动态弹性模量

动态模量是反映材料产生单位应变时所需动态应力大小的特征量,是表征岩石在高应变率下抵抗弹性变形能力的重要参数[20]。对岩石动态变形特性的分析必须建立在变形模量准确定义的基础上。然而,这种模量定义不能不加区别地复制静态测试中用于弹性模量的传统定义,我们引入以往研究中对弹性模量的定义,如表2所示。表中:σ0.5和ε0.5分别为应力-应变曲线中峰值应力50%的应力值及其对应的应变值;E1为第一类割线模量;E2为第二类割线模量。

表2 动态弹性模量计算方法Tab.2 Calculation method of dynamic elastic modulus

计算不同轴压下的各弹性模量,如图6所示。由图6可见:随着轴压的增加,第一类割线模量与第二类割线模量均呈现出先增大后减小的趋势,这与文献[19]的研究相同。两类割线模量分别代表前、后半阶段的应力-应变关系,最大值出现在轴压为10 MPa时,最小值为无轴压情况下,其中第二类割线模量的变化更大,这表明此阶段是弹性变形与塑性变形的结合。随着轴向应力从0 MPa开始增加,轴向应力对砂岩的作用由抑制裂纹发展变为促进裂纹的发展,岩石产生单位变形所需的应力从增大变为减小,故砂岩的两类动态变形模量存在先增大后减小的趋势。

图6 各弹性模量随轴压变化关系Fig.6 The relationship between elastic modulus and axial pressure

2.4 动态抗压强度

岩石受到冲击或振动等动载荷作用时发生破坏的峰值应力为岩石的动态强度。本研究的试样在动静组合加载后均发生了破坏,故此时峰值应力为砂岩在不同轴压下的动态强度。动态强度与轴压关系如图7所示。

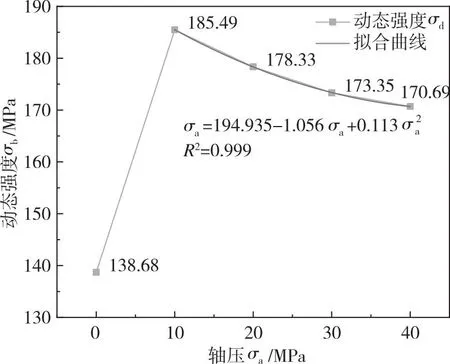
图7 动态强度与轴压关系Fig.7 Relationship between dynamic strength and axial compression

从图7可以看到:砂岩的动态强度呈现先增加后降低的趋势,这与文献[22]的研究具有相同的规律,存在轴压时岩石的动态强度拟合满足二项式分布。为了对比特定轴压作用下砂岩的动态强度相对于无轴压作用砂岩的动态强度变化幅度,定义了预应力作用下砂岩的动态强度与无轴压作用砂岩的动态强度之比为轴压-动态强度变化因子FAD,即

(2)

式中:σd为特定轴压作用下砂岩的动态强度,MPa;σd0为无轴压作用砂岩的动态强度,MPa。同时,为对比各动态强度相对于静态抗压强度的变化幅度,引入动态强度变化因子[23]FDI,即

(3)

式中:σs为静态强度,MPa。

经计算得到不同轴压下轴压-动态强度变化因子FAD、动态强度变化因子FDI,结果见表3。

表3 计算结果Tab.3 Computation result

由表3可知:随着轴压增加,轴压-动态强度变化因子FAD、动态强度变化因子FDI均先增加后减小。当试件受轴压作用时,FAD集中在1.23～1.34,轴压使得岩石的动态强度提高,但提高程度并不大;这是由于动态抗压强度具有显著的应变率效应[24],而本研究冲击气压相同,应变率并无明显的区别,所以动态强度的变化并不明显。FDI在无轴压时小于1,这符合动态强度小于静态强度的普遍情况;而轴压作用下,FDI集中在1.05～1.14,动态强度大于静态强度。

2.5 应变率与轴压的关系

根据实验数据获取轴压与最大应变率、平均应变率的关系,如图8所示。由图8可以发现,最大应变率和平均应变率随着轴压的增加先增加后减小,这与文献[25]的研究结果一致。因此,应变率不仅与动荷载大小有关,而且与岩石本身性质及静应力有关。轴压改变了岩石的性质,从而使得动载作用下岩石的应变率不同。

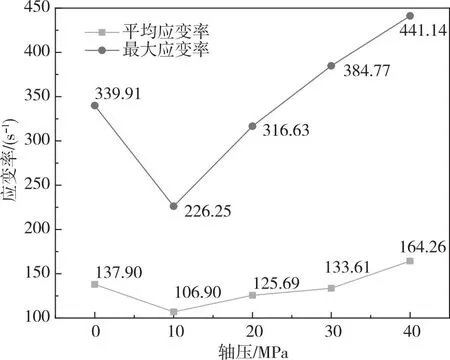
图8 应变率与轴压关系Fig.8 Relationship between strain rate and axial compression

2.6 能量演化规律

砂岩作为脆性材料,在受动载作用时总是与外界进行能量交换。能量演化规律对于深入认识不同轴压下砂岩受一维冲击动载作用下的特性具有重要意义。引入能量占比系数η表示各能量占入射能的情况,计算公式如下:

(4)

式中:η为能量占比系数;Wx为反射能WR、透射能WT或吸收能WS;WI为入射能。统计不同轴压下砂岩试样各能量占比情况反映能量耗散关系,见表4。

表4 能量耗散关系Tab.4 Energy dissipation relationship

由表4可以发现:入射能随着轴压的增加而逐渐增加,这表明入射能受轴压影响,试样在受轴压压缩的过程中,钢质压杆也受到压缩。压杆长细比极大,刚度较低,压杆内部积蓄了较大的应变能,而且轴压越大积蓄的应变能越高。当子弹头在相同的气压作用下给与压杆大致相同的动能,试样破坏开始,试样开始变形,此时压杆得到位移补偿空间,积蓄的应变能也同时释放,表现为试样受到的入射能增加。由于入射能的差异,此时探究反射能、透射能、吸收能的变化规律不能正确地反映其中的规律,故分析各能量占比的演化规律,如图9所示。

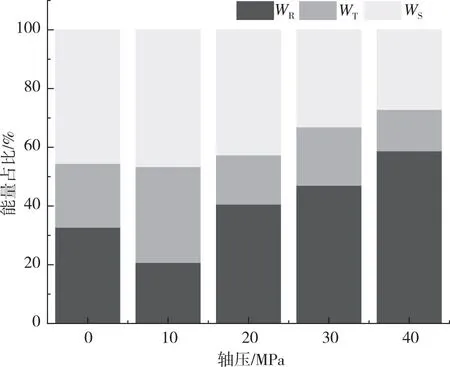
图9 能量占比图Fig.9 Energy ratio diagram

由图9可见:反射能占比呈现出先降低后增大的趋势,由无轴压时的32.73%降低至轴压10 MPa时的20.76%,之后随轴压的增加逐渐增加,轴压为40 MPa时达到最大为58.72%。吸收能占比呈现出相反的趋势,即先增加后降低的趋势,从无轴压时45.54%增加至轴压为10 MPa时的46.61%,之后随轴压的增加逐渐降低至轴压为40 MPa时的27.15%,此时为最低值。透射能占比总体上呈现出先增大后降低的趋势,在本研究中轴压的增大意味着入射能的增大,因而透射能占比随着入射能增加而先增加后降低,这与文献[26]的研究一致。

3 结论

本文利用改进的SHPB系统,研究了黔西南金矿砂岩在0.2 MPa气压下一维动静组合加载的岩石力学特性,分析了应力应变、极限应变、动态强度、弹性模量、应变率、能量演化随轴压的变化规律,主要结论如下:

1)动静组合加载试样应力-应变曲线分为压密阶段、弹性阶段、塑性破坏和峰后阶段,曲线的峰值应变在有轴压时随轴压增加逐渐增加,极限应变随轴压增加而降低,这表明轴压的增加限制了试样最终破坏时的变形。

2)第一类割线模量与第二类割线模量均呈现出先增大后减小的趋势,轴向应力对砂岩的作用由抑制裂纹发展变为促进裂纹的发展,岩石产生单位变形所需的应力从增大变为减小。

3)轴压作用时,轴压-动态强度变化因子FAD集中在1.23～1.34、动态强度变化因子FDI集中在1.05～1.14,均先增加后减小。当岩石受轴压作用时,轴压使得岩石的动态强度提高,但由于冲击气压相同,提高程度并不大。

4)最大应变率和平均应变率随着轴压的增加先增加后减小,轴压改变了岩石的性质,从而使得动载作用下岩石的的应变率不同。

5)轴压的增加使得入射能增加,反射能占比呈现出先降低后增大的趋势,吸收能占比先增加后降低,而透射能占比总体上呈现出先增大后降低的趋势。