迈向深度学习,优化复习效益*
——核心素养下高考复习“一题多解”策略探微
⦿ 河南省汝州市实验中学 辽宁师范大学教育学院 胡正波
“一题多解”是高中数学课堂教学与学习中比较常用的一种基本手段,更是高考复习中非常有效的一种教学方式.借助“一题多解”,可以有效引领复习,夯实“四基”,进而全面克服学生解题中的思维定势,有效发散数学的灵动思维,培养学生思维的灵活性与创新性,这对复习备考是非常有益的.而借助“一题多解”,能更加充分体现学生对整体知识的理解掌握情况,以及更加灵活的应用能力,也能更加有效地提升学生的“四能”,达到高效复习的最佳效益.
1 梳理整合知识,构建知识体系
借助“一题多解”策略进行高考复习与教学分析,往往可以将不同知识体系中的知识点加以合理整合,构建不同知识点之间的联系,使知识点之间“点连成线、织成面、构成体”,从而构建一个更加和谐、完整的数学知识网络体系,对于知识的全面理解与掌握,以及知识的灵活应用更加有效,从而提升数学关键能力.

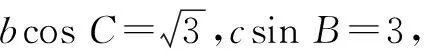
(2)若b=4,求△ABC面积的最大值.





结合同角三角函数基本关系式,有

解法2(坐标法):以AC所在直线为x轴,AC的中垂线为y轴建立平面直角坐标系xOy,则A(-2,0),C(2,0).
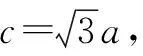
(x-4)2+y2=12(y≠0).

感悟反思:在同一数学问题中渗透多个知识点是高考命题的基本指导思想,而解题时利用不同的知识点来求解,也是必然所在.解法1中通过二次函数知识来处理,解法2中通过解析几何中的坐标知识来处理,利用各自不同的数学知识点加以切入与应用,优化解题过程,合理梳理并整合数学知识,提高课堂效益.
2 发散数学思维,培养创新意识
借助“一题多解”策略进行高考复习与教学分析,可开阔学生的眼界,形成知识的融会贯通,培养学生良好的思维品质,特别对于数学思维的变通性、灵活性、多样性与创新性等可以起到非常好的拓宽与应用效果,真正培育学生的创新意识与创新应用.
例2〔福建省泉州市2023届高中毕业班质量监测(三)数学试卷·8〕已知向量a,b,c中,|a|=1,且满足b·c=0,a·b=1,a·c=-1,则|b+c|的最小值为( ).
解法1:几何意义法.
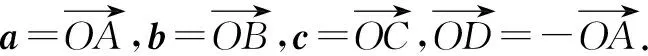
依题意并结合向量数量积的几何意义,有AB⊥OA,DC⊥DO,OB⊥OC,如图1所示.

图1
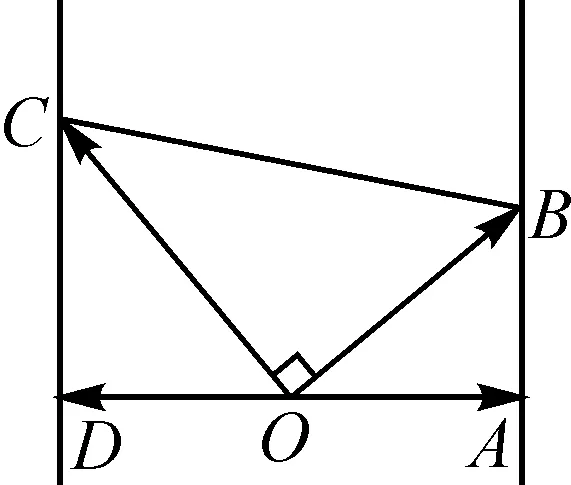
图1
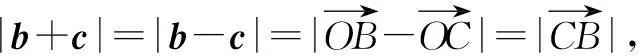
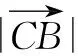
解法2:坐标法.
在平面直角坐标系xOy中,设向量a=(1,0),b=(x1,y1),c=(x2,y2),如图2所示,
因为a·b=1,a·c=-1,b·c=0,所以x1=1,x2=-1,x1x2+y1y2=0,即y1y2=1.
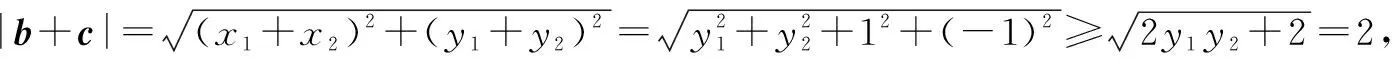
感悟反思:波利亚曾说过,掌握数学就是意味着善于解题.抓住问题的内涵与实质,从不同数学思维视角来切入与展开,是“一题多解”策略与应用的关键.解法1从几何思维切入,回归平面向量“形”的几何特征,从数形结合视角进行直观想象,解决起来更加直观简捷;解法2从代数思维切入,根据平面向量的“数”的结构属性,通过平面直角坐标系的构建,合理引入平面向量的坐标,利用平面向量中的相关要素,转化为涉及坐标的函数、方程或不等式等,进而从代数视角来数学运算与逻辑推理.
3 提升变形能力,培育逻辑推理
借助“一题多解”策略进行高考复习与教学分析,关注对问题的深入挖掘、深度学习与研究,对数学变形能力和推理有着较高的要求,结合不同的变形方向与纵深思维,展开不同的逻辑推理与解题应用,这对于逻辑推理素养的形成是非常有效的,也对推理能力的提升有很大的帮助.
例3(2023届江苏省苏锡常镇四市高三教学情况调研数学试卷·8)在数列{an}中,a1=1,其前n项和为Sn,若对任意正整数n,有Sn+1=-3an+1+an+3,且满足Sn+an>(-1)na,则实数a的取值范围是( ).

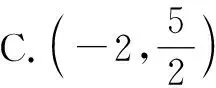
解法1:整体构建法.
令bn=Sn+an,则bn+1=Sn+1+an+1.由Sn+1=-3an+1+an+3,可得Sn+1=-2an+1-(Sn+1-Sn)+an+3,即2(Sn+1+an+1)=(Sn+an)+3,所以2bn+1=bn+3,即2(bn+1-3)=bn-3.



解法2:分层构建法(这里从略,可扫码阅读)
感悟反思:根据数列的递推关系式来分析,利用对应数列的构建来求解相应的数列通项公式是解决问题的关键,也是最重要的一个环节.解法1利用整体构建相关的数列来变形,解法2利用分层构建相关的数列来变形,进而利用对应数列的转化来分析与解决问题.在处理数列相关问题中,要挖掘问题本质,根据题设条件或所求结论加以合理变形与转化,通过概念、性质、公式等的应用,优化解题,提升效益.
其实,借助“一题多解”合理引领并指导高考数学复习以及针对性的复习备考,对教师自身的能力与水平提出了更高的要求,需要教师进行集体备课,整合团队的力量,更加有效地研究教材、考纲、考题等,进而有针对性地制定更加行之有效的教学目标,合理精选精编教学中的素材与典例,多学习、多思考、多研究、多探寻,平时要勤于实践和反思,在深度理解与深度学习的基础上开展教学与复习;同时要注意教师之间、备课组等的协同合作.

