基于“水的组成”探究实验对阿伏伽德罗定律的教学思考
任圣颖

摘要: 基于阿伏伽德罗定律被认可的历史考量,从描述方式一致性和证据推理的方法论角度,以电解水的探究实验为基础,引导学生深化认识阿伏伽德罗定律的内容和实质。分别在体积固定和体积可变的容器中呈现分子构建气体体积的过程,展现阿伏伽德罗定律“不同气体”的“不同分子尺寸”和“不同分子质量”的内涵,为学生完整地认识阿伏伽德罗定律提供可靠的途径。
关键词: 阿伏伽德罗定律; 电解水; 水的组成; 教学思考
文章编号: 1005-6629(2024)02-0092-06
中图分类号: G633.8
文献标识码: B
1 阿伏伽德罗定律被认可的历史考量
1.1 阿伏伽德罗假设的提出与接受
自从人类产生意识以来,对物质的探究便一直伴隨着人类。约公元前624~546年,古希腊哲学家泰勒斯自觉地从神话宗教世界观中摆脱出来,提出“水是万物的根源”,具有不可再分性。然而18世纪末至19世纪初的一些实验否定了水的不可再分性,在这短短的几十年内[1,2],英国科学家卡文迪许由氢气和氧气合成了水;英国化学家道尔顿发现1g氢气与8g氧气反应生成了9g水;法国化学家盖·吕萨克发现2体积氢气与1体积氧气反应生成了2体积水蒸气;英国化学家尼科尔森和卡莱尔发现电解水生成的氢气和氧气的体积比为2∶1。
道尔顿主要是从重量的角度探究氢气和氧气发生反应生成水的规律。基于倍比定律、同种电荷相斥理念以及具有猜测性的“最简法则”,道尔顿认为水的组成为HO,并写出了反应式:H+OHO。盖·吕萨克则是从体积的角度来探究氢气和氧气发生反应生成水的规律。当盖·吕萨克发现氢气和氧气反应的体积比也是简单的整数时,结合其他具有相似规律的反应,便将这种现象与倍比定律联系在了一起,并提出假设:同温同压下,相同体积的不同气体含有相同数目的“原子”。盖·吕萨克提出的假设也是根据猜测性的“最简法则”:相同体积的不同气体含有“相同”(而非其他关系)数目的“原子”即为最简单的猜测。但这个假设遭到了道尔顿的强烈反对,道尔顿认为不同原子尺寸不同,必然占据不同的空间。而且,由于研究的都是同一个反应,依据盖·吕萨克的理论,2体积氢气与1体积氧气反应生成2体积水蒸气的反应应该写为:
2H+O2HO。这将导致HO中的O是“半个原子”的矛盾。此时,依据重量的“最简法则”与依据体积的“最简法则”产生了矛盾。
1811年,阿伏伽德罗仔细考察了以上实验,认为上述矛盾的产生来自于道尔顿原子论的不完善,并正式引入分子概念,提出了两个假设。第一个假设:同温同压下,相同体积的不同气体含有相同的分子数。第二个假设:一些基本气体分子由两个原子组成。阿伏伽德罗认为氢气和氧气各由两个原子组成,水分子则由两个氢原子和一个氧原子组成[3]。2体积氢气与1体积氧气反应生成2体积水蒸气“数量上”可表示为:2N氢气分子+N氧气分子2N水分子。阿伏伽德罗假设有效地解决了“半个原子”的矛盾,但此假说并不被彼时的科学界所认可。
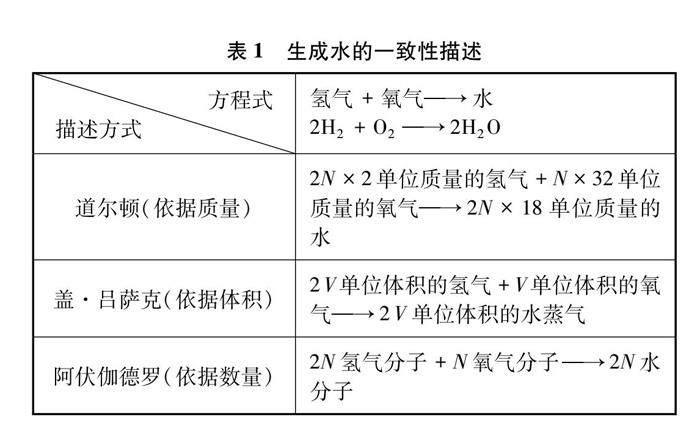
1858年,意大利化学家康尼查罗根据阿伏伽德罗假设,将氢气和氧气的分子式分别设定为H2和O2,并将氢原子的质量定为单位1,计算出氧原子的相对原子质量为16。康尼查罗敏锐地认识到如果认可阿伏伽德罗假设的内容,道尔顿、盖·吕萨克、阿伏伽德罗三位科学家对氢气和氧气反应生成水的描述将会达到完美的一致性,“水的组成”争议便会得到解决,如表1所示[4]。
1860康尼查罗在第一届国际化学会议上介绍了阿伏伽德罗假设的价值,随后阿伏伽德罗假设被科学家们所接受,阿伏伽德罗假设也变成了阿伏伽德罗定律。
1.2 阿伏伽德罗假设被接受的方法论思考
方法论是有关认识和改造世界方法的理论。在阿伏伽德罗假设被接受的过程中有以下两点值得注意。
第一,事物描述方式的一致性。描述方式一致性是指不同的描述方式都可以描述同一个事物的本质特征。各种描述方式之间具有相通性,可以相互补充、印证和转换,从而使人们能够从不同的角度深入理解此事物。在认识的不成熟阶段,各种描述方式之间往往会出现不一致性的现象。描述方式的不一致将推动着人们抛弃旧理论中的不合理因素,发展出新的理论以达到描述方式的一致性。“水的组成”被确定的过程正是如此。“水的组成”乃是规律世界的一部分,对生成水反应物的描述和电解水产物的描述都是对“水的组成”本质的描述,这些描述必然有着一致性。当盖·吕萨克从“体积化合”的角度与道尔顿从“重量化合”的角度描述“水的组成”出现不一致的时候,阿伏伽德罗提出了新的假说,以使各种描述方式达到了一致性。
第二,证据推理的重要性。作为一个从实验中总结出来的定律,阿伏伽德罗定律内容引起了科学家们极大的困惑。可以说,在某种程度上,当时的人们是通过证据(实验现象)“被迫”接受了这一事实。感性的“不同的原子尺寸不同,必然占据着不同的空间”理解起来毫无困难,但却不符合气体存在的实验现象。理性的“同温同压下,相同体积的不同气体含有相同的分子数”符合气体存在的实验现象,却不符合感性思维。虽然是“被迫”,人们终究还是接受了这个定律。这种“被迫”表现出了对实验现象的尊重,体现出了证据推理的价值,这一点和当今人们对量子科学的态度颇为相似。
以上对阿伏伽德罗定律被认可过程中方法论方面的思考促使我们在教学中将描述一致性以及证据推理融入教学设计。
2 阿伏伽德罗定律教学问题
详尽的分子动理论可以用来解释阿伏伽德罗定律的内容[5],但问题是,这超出了高中生现有的认知范围,而且我们也找不出有关类比对象使学生形象地理解这些内容。以上对阿伏伽德罗定律被认可的历史考量表明,实验现象在阿伏伽德罗定律“被迫”接受的过程中起到了关键作用。从这个角度来看待阿伏伽德罗定律教学,实验现象必然有助于促使学生接受该定律以及发展学生“证据推理”核心素养。理想的阿伏伽德罗定律验证实验,应该在同一温度和压强下,“数出”相同体积的“不同气体”的分子数是否相同,然而这一实验至少在高中阶段是不可能完成的。目前的教学,缺乏此种证据实验,此为阿伏伽德罗定律教学的第一个问题。
为了降低阿伏伽德罗定律内容的抽象性,人教版教材从物质固态、液态、气态粒子间的距离入手,通过简化的分子动理论来说明“当粒子数相同时,气体的体积主要取决于气体粒子之间的距离”[6]。然而,教学实践表明,这种处理方式并不能有效降低该内容的抽象性。这是因为学生连最基本的“气体粒子是如何占有体积”都没有准确的把握,这将导致学生理解“粒子之间的距离”时失去思维根基。如图1所示,在教学中我们总是倾向于设置一个“已经充满气体”的刚性容器来说明气体粒子之间的距离与粒子尺寸的关系。然而阿伏伽德罗定律中的“不同气体(或任何气体)”实际上有着“不同分子尺寸”和“不同分子质量”两方面内涵。刚性容器会将“不同气体与占有体积的关系”窄化为“不同分子尺寸与占有体积的关系”,隐藏“不同分子质量与占有体积的关系”,从而导致学生不能全面认识和把握阿伏伽德羅定律。如果在一个体积可变的容器里考虑“不同气体”占据空间,此时不仅要考虑气体分子尺寸,还要考虑不同气体分子具有的不同质量影响分子运动速率,进而影响分子占有体积。依据学生已有认知,同温同压下,不同质量的气体分子,必然有着不同的运动速度。那么,考虑到气体分子因运动而占有体积,同温同压下,相同数目、质量不同的气体分子会占有相同的空间吗?这个问题展现了“不同气体”的“不同分子质量”一面。教学实践表明,大多数学生都会给出否定的答案。那么,如何才能让“不同气体”展现出“不同分子质量”方面的内涵?此为阿伏伽德罗定律教学的第二个问题。
另外,在处理教材有关粒子间距离的表述信息时,如“粒子之间的距离”“平均距离”“距离等同”等,大脑倾向于在想象粒子静止的状态下进行“文字-图像”心理成像联结。此时会引发另一个问题,少部分学生会用气体粒子运动的“瞬间”静止状态去理解有关“粒子之间的距离”的教材表述。由此这部分学生认为图1两个容器中除了球形之外的空白空间不是气体粒子所占有的体积。并给出理由:这种刚性容器空间的维持和气体分子没有必然关系,即使没有气体,真空的空间也是一样存在。
由于上述教学中存在的问题,阿伏伽德罗定律对学生造成的困惑不亚于19世纪阿伏伽德罗定律提出之初——阿伏伽德罗定律是公认的教学难点。
3 问题的解决
3.1 促使学生接受阿伏伽德罗定律的证据实验
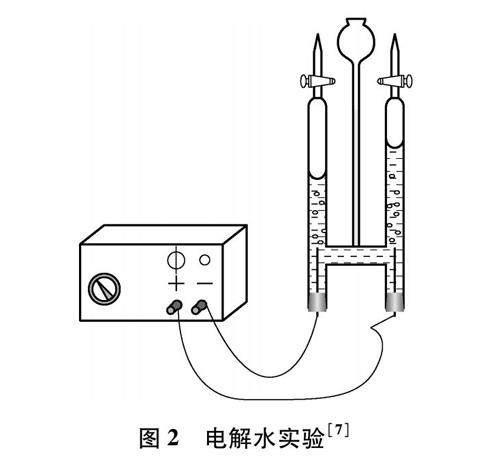
电解水实验(见图2)是人教版九年级化学课题3“水的组成”的主要内容之一。通过学习,学生已经知道电解水生成氢气和氧气的体积比为2∶1等知识点。依据描述一致性方法论,我们注意到电解水实验能够解决上文提出的阿伏伽德罗定律证据实验缺乏的问题。康尼查罗基于阿伏伽德罗定律发现道尔顿、盖·吕萨克、阿伏伽德罗三位科学家对氢气和氧气反应生成水具有描述一致性,确认了氢气、氧气、水分子分别以H2、 O2、 H2O存在。反过来,在学生已经知道氢气、氧气、水分子分别以H2、 O2、 H2O存在的情况下,依据描述一致性方法论,则可以通过电解水实验来推出阿伏伽德罗定律内容(见下文简要教学设计)。
3.2 促使学生接受阿伏伽德罗定律的简要教学设计
[教师]带领学生回顾图2电解水实验,提出问题:为什么电解水产生的氢气与氧气体积之比为2∶1?
[学生]对上述问题进行思考,讨论。一般情况下,学生会将答案归于“生成的氢气与氧气为2∶1”上,这种不严谨、来自直觉的答案已经暗含着阿伏伽德罗定律的萌芽。
[教师]在“生成的氢气与氧气为2∶1”的答案中,是指分子数量、分子质量,还是只有体积为2∶1?
[学生]从实验现象来看,生成氢气和氧气的体积之比为2∶1;从化学方程式来看,生成氢气和氧气的分子数量之比是2∶1。
[教师]氢气和氧气的体积之比与分子数量之比都是2∶1,这是一种巧合,还是一种必然呢?请同学们填写下列表格2,对电解36g水的电解产物进行质量、物质的量、数量及体积比的描述。
[教师]在填写表2之前给予学生“描述方式一致性”的解释和说明。
[学生]根据已有的知识,得出质量和数量(或物质的量)的描述方式具有一致性。但是按照体积的描述方式是否能够纳入这种一致性,即便在一些九年级的教学中已经有所补充[8],但大部分学生依然会有比较大的疑惑。这个疑惑正是指向了阿伏伽德罗定律内容。
[教师]结合表1,呈现图3进行讲解:电解36g水生成的氢气和氧气分子数量比为2∶1,体积比也是2∶1,将得到的氢气体积设为2V,氧气的体积设为V,接下来将氢气体积平均分为V两部分,那么V体积氢气和V体积氧气所含的分子数一样多吗?
[学生]得出答案:V体积氢气和V体积氧气所含的分子数一样多。
[教师]V体积氢气和V体积氧气所含的分子数一样多,是在同温同压的条件下吗?
[学生]在同温同压的条件下。
[教师]科学家们做了大量的实验,发现在相同的温度和压强下,不仅仅是氢气和氧气,而是相同体积的任何气体都含有相同数目的粒子。这就是令人感到不可思议的阿伏伽德罗定律。
[学生]为什么相同的温度和压强下,相同体积的任何气体都含有相同数目的粒子?不同的气体分子大小不一,肯定占据着不同的体积。
[教师]虽然同学们感性上不能认同,但作为证据的实验现象表明阿伏伽德罗定律内容是正确的,因此我们必须理性地接受这个定律。证据推理的价值之一就是帮助人们用理性战胜感性。同学们在以后的学习中,必然也会遇到类似的情形,比如不可思议的量子理论,同学们必须先要根据实验现象理性地接受此理论。同学们的疑惑将会在接下来的环节中得到解释。
说明:在本教学环节中,从产物“一致性”描述为切入点引出阿伏伽德罗定律是必要的。描述方式的一致性将不同气体的相同体积和相同分子数目“粘结”在了一起。这样的教学活动围绕着水的本质特征“水的组成为H2O”展开,有利于学生将阿伏伽德罗定律和已有认知产生联系。另外,电解水实验,仅为“任何气体”中的一个实验,教师可再呈现电解饱和食盐水的实验,从化学方程式中氢气和氯气物质的量之比和收集到的两种气体体积比都是1∶1来进一步验证阿伏伽德罗定律。
3.3 思考气体分子如何占有体积,解释阿伏伽德罗定律
通过上述教学环节,学生认识到阿伏伽德罗定律的正确性有着证据的支撑,但是学生对这个定律的内容一定是感到“困惑不已”,再加上“不同气体”展现出“不同分子尺寸”和“不同分子质量”两方面内涵的教学需要,所以有必要结合教材呈现“气体占有体积”的构建过程,本文建议从以下两个步骤实施。
步骤一:呈现固定体积容器(刚性容器)内的气体体积构建过程,展现“不同气体”的“不同分子尺寸”方面内涵(如图4所示)。在固体体积的容器内,两种固态物质随着温度升高变成液态、气态。虽然这种方法让学生看到了分子从固态、液态到气态如何构建体积的过程,但由于刚性容器已经限定了体积的原因,这种方法不能将“不同分子质量与占有体积关系”问题暴露出来,也不能完全消除“静态”思考分子间距离的思维,少部分学生认为刚性容器本身就有空间,气态粒子未必一定去占据,由此这部分学生认为图4气态容器空白处体积没有被气体分子所占据。
步骤二:呈现体积可变容器内的气体体积构建过程,着重展现“不同气体”的“不同分子质量”方面的内涵以及消除学生“静态”思考分子间距离的思维。为了进一步降低抽象性,本研究以“蜜蜂分子”主动构建体积来说明此内容。选择“蜜蜂分子”的主要原因是学生对蜜蜂的快速飞行有着感性认识,可以辅助学生理解气体分子的运动,如图5所示。
3.4 分子构建气体体积的简要教学设计
[教师]相信同学们对阿伏伽德罗定律一定是感到“困惑不已”。以氢气和氧气为例,就像同学们刚刚提出的问题,氢气和氧气的原子半径大小不一,数目相同的它们怎么会占据相同的空间呢?我们用大小不同的球分别代表氢气和氧气分子。在一个固定体积V的容器里,请同学们来画一下气体分子如何占有空间。
[教师]利用学生所画的“紧密堆积在一起,占据不同空间”或“松散堆积在一起,但依然占据不同空间”图,结合图4进行讲解:如果将温度降低到一定程度,氢气和氧气将会变成固态或液态,此时分子间距离小,相同分子数目氢气和氧气所占据的体积肯定是不同的。而在气态下,气体分子是不断高速运动着的,彼此相互碰撞,气体分子间距离很远。请同学们结合教材表述,观察图4的右边部分,想一想,同温同压下,相同数目的氢气和氧气所占据的体积相同吗?
[学生]大部分学生认为相同,少部分学生认为图4右半部分除了球形之外的空白空间不是氢气和氧气所占有的空间,氢气和氧气所占据的体积不相同。
[教师]呈现图5,讲解:设想在常温常压下,有多只从冷冻箱中取出的“冻僵的”蜜蜂分子,以4只为代表,放入一个体积可变的球形容器中。刚开始,“蜜蜂分子”由于冻僵了而保持静止不动,此时由于外界大气压的原因,容器将紧紧包裹着“蜜蜂分子”,不会有多余的空隙。接下来由于外界温度较高,能量通过容器壁传递给“蜜蜂分子”,“冻僵”的“蜜蜂分子”开始慢慢升温。在刚开始阶段,“蜜蜂分子”只能在被束缚的没有多余空间的容器中相互间缓慢爬行,被束缚的容器形状会因为“蜜蜂分子”爬动而变化,但由于外界大气压的原因,“蜜蜂分子”还是紧紧被束缚,但活动范围肯定比“冻僵”的“蜜蜂分子”占有的空间大一些。最后,“蜜蜂分子”获得了足够的能量,“蜜蜂分子”开始飞起来。由于“蜜蜂分子”的飞速极快(400m/s),加上相互撞击,此时“蜜蜂分子”将以“云”形式占据着一定体积V。虽然容器中只有4只“蜜蜂分子”,却能占据比它们本身体积大的多的空间,这是因为“蜜蜂分子”能够在极短时间内达到图示空间任一位置。容器体积还来不及坍塌,即被“蜜蜂分子”迅速占据(灰色表示瞬间到达某一位置的“蜜蜂分子”)。显然,“冻僵的蜜蜂分子”、“能够爬动的蜜蜂分子”、“快速飞动的蜜蜂分子”分别相当于物质的固态、液態、气态。请同学们根据以上讲解,思考图4右半部分除了球形之外的空白空间是否为氢气和氧气所占有?
说明:图5能够促使学生“动态”思考“气体分子如何占有空间”。因为此时容器不再是刚性的,只要“蜜蜂分子”停止快速飞动,“蜜蜂分子”所占据的体积立即就会“塌陷”到固、液态,这就巧妙地实现了“动态”思考“粒子之间的距离”与“占有体积”关系,图4气态容器空白处体积是否被气体分子所占据的问题也就被消解掉了:在气态时,气体分子将在极短时间内可以达到图4刚性容器空间的任一位置。至此,学生就建立起来了气体分子占有空间与分子间距离“动态”的联系,扭转了“静态”的思考方式。
通常,在讲解“蜜蜂分子”占据空间时,很多学生还会提出这样一个问题(如果学生没有提出,则需要教师提出):同温同压下,如果将“蜜蜂分子”换成相同数量的“苍蝇分子”(大小、质量不一),“苍蝇分子”所占据的空间与“蜜蜂分子”占据的空间会相同吗?这一问题极具价值。首先这个问题再一次证明了阿伏伽德罗定律内容极具抽象性的特点。只要分别将“蜜蜂分子”和“苍蝇分子”看成氧气、氢气,这个问题的答案就指向了阿伏伽德罗定律内容。因此教师需要再次用电解水的实验现象(证据)促使学生接受此定律,即在同温同压下相同数量的氧气和氢气会占据相同的体积。如此,整个教学便可构造成为逻辑上可解释的“闭环”。更为重要的是,学生的这个问题将“刚性容器”隐藏的“不同分子质量与占有体积关系”问题完全暴露了出来,通过对此问题的探讨,学生将能全面、透彻地认识阿伏伽德罗定律的内容。这个问题探讨之后,教师便可引导学生结合教材表述,总结出气体体积与气体粒子数量、大小、质量及粒子间距离的关系。
4 结语
阿伏伽德罗定律内容超越了学生已有的分子尺寸、分子质量与占有空间关系的直觉,成为了教学中一个难点。而且由于难以找到类比的对象以及不能详尽介绍分子动理论,我们对于阿伏伽德罗定律的抽象性总有种无能为力之感。本研究利用电解水探究实验,解决了阿伏伽德罗定律教学缺乏实验证据的问题,让学生体会到了证据推理在理性战胜感性方面的价值;在体积可变的容器中呈现分子构建气体体积的过程,将刚性容器隐藏的“分子质量与占有体积的关系”的问题暴露了出来,为学生完整地认识阿伏伽德罗定律提供了可靠途径。
参考文献:
[1][4]Sarikaya M. A view about the short histories of the mole and Avogadros number [J]. Foundations of Chemistry, 2013, 15(1): 79~91.
[2]Cerruti L. The Mole, Amedeo Avogadro and Others [J]. Metrologia, 1994, 31(3): 159~166.
[3]Murrell N J. Avogadro and His Constant [J]. Helvetica Chimica Acta, 2001, 84(6): 1314~1327.
[5]傅献彩, 沈文霞, 姚天扬等. 物理化学(上册)[M]. 北京: 高等教育出版社, 2006: 17.
[6]王晶, 郑长龙主编. 普通高中教科书·化学(第一册)[M]. 北京: 人民教育出版社, 2019: 52.
[7]姜跟华. 电解水实验的再改进[J]. 化学教学, 2023, (3): 73~75.
[8]庞刚志, 杨玉琴. “教、学、评”一体化下的学案导学教学实践——以人教版九年级《化学》“水的组成”为例[J]. 化学教学, 2021, (10): 53~59.

