一道高考真题的探究拓广及其命制背景分析
重庆市渝北中学校(401120) 杜 鹏
1 试题及解法
2.当直线MN斜率不存在时,经验证同样满足题意.
综上,P在定直线上.
评析解决本问题时,涉及到“非对称韦达定理”的处理.对于方法一,直线和曲线联立后,得到一个关于y的方程,此时y1+y2与y1y2的关系比较明显,可以直接代换出来,问题进而解决.对于方法二,由于联立时,直线和曲线联立后,得到一个关于x的方程,此时x1+x2与x1x2的关系就非常不明显,对于寻找这两者的关系,一般可以采取凑配或者待定系数的方法.采用凑配的时候可以从不同的角度进行,第一个角度是让x1+x2与常数m结合,使得x1+x2+m这个式子的分子出现与x1x2分子一样的结构,即能够产生一个k2+1 的式子,具体过程如下:;只需令8-m=4m,得:;这就是我们为一个要加一个常数的原因.第二个角度是让x1x2与常数n结合,使得:x1x2+n这个式子的分子出现与x1+x2分子一样的结构,即产生一个k2的式子,具体过程如下:;只需令4n-16=0,得:n=4;至此就弄清楚凑配的时候为什么要加常数4.待定系数法,其实就是在凑配方法基础上的一种提炼,没有凑配法的思考过程,直接是不容易想得待定系数法的,只有对凑配法有了足够的思考,才会想到它的本质就是待定系数法.对于法三,利用点在曲线上的性质,将其中一个非对称的表达式转化为对称的表达式,就可以把非对称结构转化为对称的结构,这样问题就迎刃而解.关于“非对称韦达定理”更多的处理方式,可以参考文献[1].
2 探究和拓广
3 命制背景
本题的命制具有高等几何的背景,其主要涉及的内容是极点极线的相关知识.虽然作为中学生不需要掌握极点极线的相关知识,这个不属于高考要求的范围,但是作为高中数学教师有必要了解极点极线的相关知识,了解掌握相关知识后,对一些圆锥曲线里面的定点和定直线问题将会有一个更深层次的理解,对这些题目为什么这样命制,这样命制的原理将会有一个更加清晰和深刻的认识,下面我们来看极点极线的定义.
定义1(几何定义)如右图,P是不在圆锥曲线上的点,过P点引两条割线依次交圆锥曲线于四点E,F,G,H,连接EG,FH交于M,EH,FG交于N,则直线MN为点P对应的极线.若P为圆锥曲线上的点,则过点P的切线即为极线.
由右图可知,同理PM为点N对应的极线,PN为点M所对应的极线,三角形MNP称为自极三角形.若连接MN交圆锥曲线于点A,B,则PA,PB恰为圆锥曲线的两条切线.
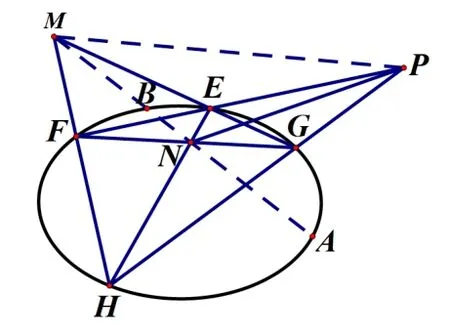
特别地,对于中心在原点的二次曲线mx2+ny2=1(mn0),与点P(x0,y0)对应的极线方程为mx0x+ny0y=1.
关于更多的极点极线相关性质,可以参考文献[2].
下面具体用几个高考真题实例,来加以说明这些题目是如何以极点极线为背景命制的.
例1题目见文章开头题目.
(1)求E的方程;
(2)证明: 直线CD过定点.
例3(2011 年四川高考数学第21 题) 椭圆有两顶点A(-1,0),B(1,0),过其焦点F(0,1) 的直线l与椭圆交于C,D两点,并与x轴交于点P,直线AC与直线BD交于点Q.
4 小结反思
《普通高中数学课程标准(2017 年版2020 年修订)》中明确指出:“高中数学课程以学生发展为本,落实立德树人根本任务,培育科学精神和创新精神,提升数学学科核心素养”[3].在平时的解题教学中,为了达到以上目标,可以通过下面两个方面来落实.
4.1 重视基础和通性通法
2023 年新高考II 卷第21 题,满分12 分,其中第(1)问4分,第(2)问8 分,重庆市194394 位考生的平均分是3.28 分,得分率仅为27.33%.出现这一问题的原因,一方面学生的基础出了问题,第(1)问就有4 分,肯定有部分学生没有作答正确;另外一方面,学生对解决解析几何问题的通性通法掌握不够,第(2)问的直线设法,有一定数学思维的同学都会选择x=my-4 这样来设直线,在后面处理非对称结构就会轻松许多,得分就比较容易.如果选择了另外一种设直线的方式,问题的难度将会变大,得分将困难得多.在教学中,一定需要注重学生基础知识的掌握,同时也需要加强数学通性通法的理解和运用,通性通法不是一句口号,而是教会学生思考数学,运用数学,掌握数学的内在规律和本质.
4.2 适当拔高并探究拓广
著名数学家波利亚说过:“在你找到第一个蘑菇(或做出第一个发现)后,要环顾四周,因为它们总是成堆生长的”[4].在教学过程中我们发现,很多习题都隐藏着更进一步的一般性的结论,或者具有高等数学的背景.这个时候需要教师引领学生对这些题目进行一题多解,变式研究,类比拓广,有了对这个题目本质的深刻认识,就可以去查阅相关资料看是否有高等数学的背景,那么此时对这个问题就会有一个全面系统的了解.在探究问题的过程中,可以训练学生的思维能力,提升他们的核心素养,注重对学生探究意识的培养应该是每一位高中数学教师的必备素养.

