正确区分超几何分布和二项分布
——从一道高考真题错解谈起
河南省平顶山市第一高级中学(467000) 米召奎
在新高三的教学中,让学生练习了2023 年高考数学全国甲卷第19 题,对于第一小问,学生们给出了三种不同解法,争论激烈,甚至有同学拿出某考卷给出的“标准答案”,以此证明自己的解法的正确性.这不由的让我反思,如何在教学中让学生能正确区分超几何分布和二项分布.
1 真题呈现
题目(2023 年高考数学全国甲卷第19 题)一项试验旨在研究臭氧效应.实验方案如下: 选40 只小白鼠,随机地将其中20 只分配到实验组,另外20 只分配到对照组,实验组的小白鼠饲养在高浓度臭氧环境,对照组的小白鼠饲养在正常环境,一段时间后统计每只小白鼠体重的增加量(单位: g).
(1)设X表示指定的两只小白鼠中分配到对照组的只数,求X的分布列和数学期望;
(2)略.
本题主要考察了离散型随机变量的分布列以及独立性检验问题.第二问没有分歧,下面主要研究第一小问的解法.
2 解法赏析
解法1一只小鼠要么分在实验组,要么分在对照组,有2 种分配方案,两只小白鼠总的分配方案为2×2=4 种,其中两只小白鼠全部分配到试验组有1 种情况,有一只分配到对照组有2 种情况,全部分配到对照组的有1 种情况.则X的可能取值为0,1,2.由古典概型的概率计算公式可得:.所以X的分布列如表1:

表1 随机变量的分布列
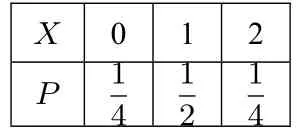
表2 随机变量的分布列
解法3依题意,X的可能取值为0,1,2.则
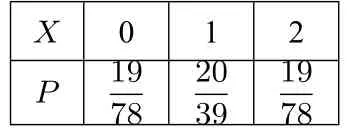
表3 随机变量的分布列
3 寻根求源辨真假
三种做法的期望一样,但是计算方法不同,概率分布列也不同,孰对孰错? 我们不妨回归教材.
3.1 教材中的定义
二项分布: 一般的,在n重伯努利试验中,设每次试验中事件A发生的概率为p,用X表示事件A发生的次数,则X的分布列为表4:
表4 二项分布列

如果随机变量的分布列具有上述形式,则称随机变量服从二项分布,记作X~B(n,p).
超几何分布: 一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则P(X=k)=k=0,1,2,···,m,则X的分布列为表5:

表5 超几何分布列
其中m=min{M,n},且n≤N,M≤N,n,M,N ∈N+;
如果随机变量的分布列具有上述形式,则称随机变量服从超几何分布,记作X~H(N,M,n).从定义可以看出:
(1)二项分布中的试验是重复试验;超几何分布中的试验是古典概型的随机试验.
(2)二项分布中用的是有放回抽样,所以每次抽取条件不变;超几何分布中用的是不放回抽样.
(3)二项分布进行的试验无需知道总体数;超几何分布在试验过程中必须给定总体数,而且总体必须由数目明确的“正品”与“次品”两类构成.
(4)二项分布每一次试验只有两个对立的结果A或,即事件要么发生,要么不发生;超几何分布每一次试验的结果数较多,比如在有M件次品的N件产品中任取1 件产品,不同的结果有种.
(5)二项分布中离散型随机变量X表示这n次独立重复试验中事件A出现的次数,即成功次数.所以事件X=k表示n次独立重复试验中事件A出现了k次,事件出现了n-k次;超几何分布中离散型随机变量X表示抽取出的这n件产品中的次品数.所以事件X=k表示抽取的n件产品中有k件次品,n-k件正品.
二项分布中进行的是独立重复试验,满足独立事件的概率乘法公式,所以事件X=k发生的概率P(X=k)=,其中k=0,1,2,···,n.
超几何分布进行的随机试验是满足古典概型的随机试验,所以事件X=k发生的概率P(X=k)=其中k=0,1,2,···,m,m=min{M,n}.
(7)二项分布概率计算会在题设中暗示给出或者可求出事件A发生的概率p.
超几何分布概率计算会在题设中给出抽样个数n、总体数N,会给出或可求出总体中两类产品中的“次品”数M.
3.2 教材中的问题与案例
在现行新教材人教A 版《选择性必修》第三册的7.4.2节,有这样一个问题: 已知100 件产品中有8 件次品,分别采用有放回和不放回的方式随机抽取4 件,设抽取的4 件产品中次品数为X,求随机变量X的分布列.这个问题旨在让学生通过具体情景感知,如果采用放回抽样,那么抽取的4 件产品中次品数x服从二项分布,如果采用不放回抽样,虽然每次抽到次品的概率都是0.08,但是每次抽取不是同一个实验,而且各次抽取的结果也不独立,不符合n重伯努利试验的特征,x服从超几何分布.也就是说,有无放回是区别二项分布和超几何分布的重要特征.
在教材的页这样一个习题: 一个车间有3 台车床,它们各自独立工作,设同时发生故障的车床数为X,在下列两种情形下分别求X的分布列
(1)3 台车床型号相同,它们发生故障的概率是20%.
(2)3 台车床中有A 型号2 台,B 型号1 台,A 型号车床发生故障的概率是10%,B 型号车床发生故障的概率是20%.
在这里并没有明确的说明是“有放回”还是“无放回”的抽取,但是,(1)中车床型号相同,且发生故障的概率相同,可以理解为在相同试验条件下进行3 次独立试验,满足n重伯努利试验的条件,所以x服从的是二项分布,而在(2)中车床分不同的型号,有差异,每种型号车床发生故障的概率有差异,那么发生故障的概率跟车床有关,所以服从超几何分布.
3.3 真假辨析
之所以产生不同的分布列,分歧在于如何随机抽取小白鼠.现在回看高考真题的三种解法,就会发现思考的视角不同,得到的答案也不同.
解法1 的视角是把研究的对象放到指定的两只小白鼠上,指定的两只小白鼠中每一只被抽到的可能性相等,就像抛掷两枚质地均匀的硬币,出现正面向上或反面向上的机会均等,按照古典概型罗列包含的样本点空间为Ω={(正正),(正反),(反正),(反反)}四种情况.
解法2 的视角是把研究的对象放到两个组上,即实验组和对照组,实验者首先将小白鼠编好号码为01 至40,然后对每个号码,在实验组和对照组中随机分组.这是完全随机化实验.指定的两只小白鼠被分配到对照组之间是独立的,抽两只小白鼠当作2 次独立重复实验,因此服从二项分布,即
解法3 的视角是把研究对象放到构成对照组的20 个个体上,也就是说从40 只小白鼠中抽取20 只分配到对照组即可,对于指定的两只小白鼠被抽到的只数服从超几何分布.
由上分析可见,三种解法都是正确的.事实上,三种解法涉及的是一个贝特朗悖论问题,即样本空间不同,造成不同的计算方法.那么,为什么视角不同而得到的期望都一样呢?根据期望计算公式,对于二项分布而言,若X~B(n,p),则E(X)=np;对于超几何分布而言,若Y~H(N,M,n),则.事实上,在二项分布中,,所以这就很容易理解为什么不同算法得到的期望是一样的.另外有趣的是,对于不放回抽样,当总体数目比较大而抽取的样本数较少时,每次抽出产品后,次品率近似不变.这样就可以近似看成抽样的结果是相互独立的,抽出产品中次品件数近似服从二项分布.这也往往是很多同学对两种分布容易混淆的地方.
4 正确区分二项分布与超几何分布
一般的,我们认为辨别随机变量的分布列是超几何分布还是二项分布,有重要的两点,其一是看总体数大小,其二是有无放回.当总体数目较大或者没有给出时,或者是无放回抽取时,属于二项分布,反之,为超几何分布.
事实上,很多时候,学生面临的很多试题中,并没有明确说明是有放回还是无放回抽取,这就造成很多学生无法正确辨别采用什么分布,从而做错.究其原因,就是没有考虑实际,忽略了语言的隐含性与暗示,例如当试题中出现“从流水线上抽取”或者“每次试验以事件A发生的频率近似作为概率等”都是隐含的告知每次试验事件A发生的概率相同.
在实际的工厂产品检验中,若N件产品中共有M件次品(N >1,M >1,N >M),则不放回地抽样中,第一次抽到次品的概率为,而第二次抽到次品的概率与第一次抽到的是否为次品有关.若第一次抽到的是次品,则第二次抽到次品的概率为;若第一次抽到的不是次品,则第二次抽到次品的概率为.在实际工作中,产品检验一般都采用不放回抽样,因此要计算n次抽取中恰好得到k件次品的概率,应采用超几何分布的概率公式.但是此公式需要知道总体的容量,数值计算比较复杂,不过当N相对M来说很大时,都可以近似为,此时不放回抽样与放回抽样是差不多的,故超几何分布近似于二项分布.因此可用二项分布的计算公式近似,这样可以大大节省计算量,所以当一批产品数量很大的时候,我们可以把取得某类样本的频率视作取得这类样本的概率,用二项分布近似代替超几何分布[1].
因此判断两种分布时,不能机械地以抽样方法来判定,对于总体数N很大的这种抽取,尽管是无放回抽样,但超几何分布已经近似为二项分布了,我们都把它看成是n次独立重复试验,按照二项分布来解题.
5 教学启示
著名数学教育家波利亚认为:“数学教学的第一要务就是要加强解题训练”,教师通过例题习题,可以让概念具体化,通过例题习题及时纠正学生对概念理解的偏差,这就要重视教材,从教材出发,通过教材中的经典案例,剖析超几何分布和二项分布的内在联系与本质区别,例如对于没有明确指明是有放回还是无放回的流水线上抽取产品,使学生能准确辨别“从生产的产品中任取n件”属于二项分布,而“从抽取的样本产品中任取n件”属于超几何分布.
让学生在具体的情景中抓住关键,从而提高辨识,避免混淆不清.毕竟教材中的例习题是经过家精心构思、反复推敲后选定的,是教材知识点的辅助和补充,有利于学生们把握数学概念和内涵.所以,在教学中,尤其是概率统计这一部分,要精选例题、习题,从而让学生深刻理解不同分布的区别与联系,面对问题的时候,才有有的放矢提高解决问题的准确性.

