借题发挥,促进深度教学
——教材例习题拓展的思考
广东省佛山市高明区第一中学(528500) 王顺耿
福建省闽南师范大学数学与统计学院(363000) 赖俊聪
教材中的例习题是教育专家精挑细选,又经过反复锤炼的典型问题,有着重要的教学价值.“源于教材、高于教材”是高考命题中遵循的一个重要原则,高考试题中总有教材例习题的影子.深度教学是基于知识的内在结构,帮助学生在学习中深入理解和掌握所学内容,培养学生提出问题、分析问题和解决问题的能力,提升数学核心素养,克服学生对知识的表层学习,对知识的简单占有.因此,日常教学中,教师应该直击教材本源,借题发挥,加强对教材例习题的研究和反思、拓展和升华,去促进深度教学.
如何去挖掘教材例习题的价值呢? 本文从问题本身的内容和结构出发,探究教材例习题拓展的路径,促进学生深度学习.
1 教材例习题拓展路径
一个数学问题由问题条件和问题结论两部分构成,问题条件中,存在很多基本构件、以及连接构件显性或隐形的关系和关联.元件,是在同类装置中可以互换使用的零件,为小型机器、仪器的组成部分,它的重要特性是能在同类装置中互换使用.基于元件这一特性,本文借用“元件”概念来阐述数学问题的构成和拓展,将数学问题隐喻为机器,条件和结论中的基本构件看作机器的元件.
解题教学中,将数学问题条件和结论中的基本构件作为数学问题的“元件”,通过对数学原题的元件以及元件间相互关系的拆与组,分与合、转与换,用已知或潜在的数学关系、基本原理作为“支架”,构造出一种相关的新的数学对象、数学形式,推陈出新形成元件重组的数学新题进行数学解题教学,可以使学生认清题目的骨架和构件、迁移和转化,锻炼学生分析和解剖数学试题,提升解题能力,培养学生思维能力,尤其是对创造性思维能力开发有其独特作用.
数学问题的深度挖掘,可以从问题条件和问题结论两个方面思考.首先,改变问题条件,可从元件域、元件型、元件联和元件语四个方向着手: 其中,①元件域是指问题条件中“元件”的变化区域,可以是反映数量关系的“元件”的变化范围,如线段、字母、角度等大小的量化限定,也可以是反映空间形式的“元件”,如点、线、面在空间中的位置变化限定和位置关系;②元件型是指问题条件中“元件”的类型,如线段、三角形、方程、函数等;③元件联是指问题条件中各“元件”之间或显或隐的结构关联和逻辑关联、以及空间形式的位置关联,如两角互补、两数之积为常数、直线与圆相切等;④元件语是指数学语义转换,如知识情景转换或数学语言表达的转换(文字语言、符号语言和几何语言间的转换),将问题中的“元件”信息合理地转换成另一种等价的“元件”信息,使题意更易理解,让问题的已知条件“元件”和结论“元件”走得更近一些,或使结论“元件”更适合已知条件“元件”,以利于问题解决.其次,改变问题结论,可从目标象、目标层和目标呈三个方向着手: 其中,⑤目标象是指问题结论的目标对象,如求解对象为三角形面积、函数的最值、数列通项等;⑥目标层是指问题结论的设问层次,增加设问层次可以增加检测点,使设问多向化或为了降低难度使设问梯度化,减少设问层次作用相反;⑦目标呈是指问题结论的呈现方式,可以根据需要对问题结论改头换面,以新的设问形式来呈现问题,设问方式包括证明、计算、判断、论述、设计等形式.
数学例习题的拓展路径,可以通过改变数学问题条件和结论中的七个形式中任何一个形式、两个或两个以上形式组合的综合方式,得到不同的数学新题.
2 教材例习题拓展例示
下面选取教材中的一道例题,根据上述的拓展路径来体会具体操作,限于篇幅部分简单的新题略去求解或证明过程.
普通高中教科书《数学》(2019 年人教A 版) 必修第一册5.5.2 节,P227 例题10:如图1,在扇形OPQ中,半径OP=1,圆心角,C是扇形弧上的动点,矩形ABCD内接于扇形.记∠POC=α,求当角α取何值时,矩形ABCD的面积最大? 并求出这个最大面积.
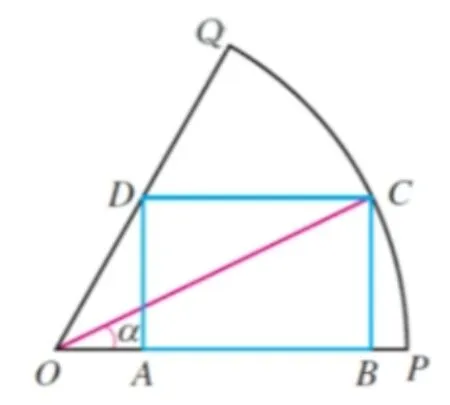
图1
分析例题,仔细梳理题中元件及元件间的关联:
条件元件(1)半径为1 的扇形,(2)圆心角(3)矩形ABCD内接于扇形,(4)∠POC=α;
元件关联(1)矩形ABCD内接于扇形,且一边AB在半径OP上,(2)隐性关联: 矩形的面积=长×宽;
求解结论矩形ABCD的面积的最大值.
本例题求解难点是矩形ABCD的面积函数模型的构建和模型化简求解,下面依前文提出的拓展路径对例题进行挖掘:
2.1 变元件域
创编意图讲解例题前,为辅助例题解答,先做铺垫,设置具体角度,这样更易过渡到例题的一般性.具体解答过程略去.
新题1[1]如图1,在扇形OPQ中,半径OP=1,圆心角C是扇形弧上的动点,矩形ABCD内接于扇形.记∠POC=α,求当角α取何值时(用θ表示),矩形ABCD的面积最大? 并求出这个最大面积.
解在RtΔOBC中,OB=cosα,BC=sinα;在RtΔOAD中,
设矩形ABCD的面积为S,则
创编意图: 将问题变成开放性、探究性问题,与例题比较,得出问题一般性规律: 当角α为∠POQ=θ一半时,即C为中点时,矩形ABCD的面积取得最大值.引导学生看透问题本质,提升了对例题的认识,促进学生深度学习.
2.2 变元件型
将例题条件元件(1)改为等边三角形,或将元件(3)改为正方形,可得新题.
新题2如图2,在等边ΔOPQ中,OP=1,C是PQ上的动点,矩形ABCD内接于等边ΔOPQ.记∠POC=α,求当角α取何值时,矩形ABCD的面积最大.

图2
解法1如图2,在ΔOPC中,由正弦定理得
创编意图线段OC由定到变,深度增加;解法一依照教材方法建立了矩形的面积模型,模型复杂难解,而解法二间接设参,解答简易快捷;让学生体会元件型的改变会引起解决方法的改变,要因变而变;同时得到与新题1[1]同样的规律: 当角α为∠POQ一半时,即C为中点时,矩形ABCD的面积取得最大值.
新题2[1]如图1,在扇形OPQ中,半径OP=1,圆心角C是扇形弧上的动点,矩形ABCD内接于扇形.记∠POC=α,求当tanα取何值时,矩形ABCD为正方形,并求出这个正方形的面积.
创编意图使学生体会正方形时面积不一定为最大,消除定势思维.
2.3 变元件联
将元件关联(1)矩形ABCD位置改变,或将长方形改为圆,面积关联改为圆的面积公式,可得新题.
新题3如图3,在扇形OPQ中,半径OP=1,圆心角C是扇形弧上的动点,矩形ABCD内接于扇形.记∠POC=α,求当角α取何值时,矩形ABCD的面积最大? 并求出这个最大面积.
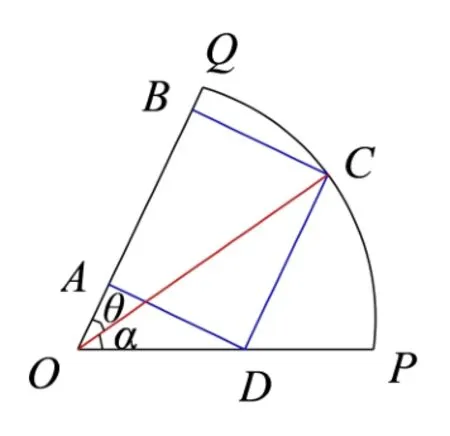
图3
创编意图由于对称性,让学生体会矩形ABCD一边在OP边上和在OQ边上不会影响结果;同时体会条件结构变了,解法也应改变,不要简单照抄教材思路,因变而变则不难.
2.4 变目标象
改变原题中的求解目标,将矩形ABCD的面积问题改为矩形ABCD的周长问题,可得一新题.
创编意图改变求解目标,从不同视角加深对原题的进一步认识,开阔了学生对问题研究的思路.
2.5 变目标层
添加设问层次,使求解问题梯度化,降低了问题的难度,同时也增添了检测点.
新题5如图1,在扇形OPQ中,半径OP=1,圆心角,C是扇形弧上的动点,矩形ABCD内接于扇形.记∠POC=α,求
(1)AB、BC的长;
(2)求矩形ABCD的面积S(α)关于α的解析式;
(3)当角α取何值时,矩形ABCD的面积最大? 并求出这个最大面积.
创编意图为了降低题目求解难度,搭建脚手架,问题设置层层相扣,使问题梯度化.具体解答过程略去.
2.6 变目标呈
将求解目标改头换面,以新的设问形式来呈现问题.
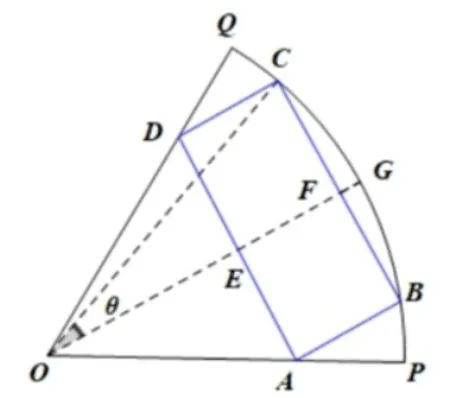
图4
创编意图将例题创编为开放性问题,加大问题解决的难度,增添了探究的乐趣.
以上展示的是单一改编,实际课堂教学中,更多情况下需要的是复合改编,即通过改变两种或两种以上形式而得到创编题.譬如通过改变例题元件(1)和元件(3)以及求解结论,可以得到另一情景下的新题7.
新题7如图5,等边ΔOPQ中,OP=1,在ΔOPQ内作第1 个正方形A1B1C1D1,再在等边ΔD1C1Q内作第2个正方形A2B2C2D2,…如此下去,判断这些正方形边长有什么规律,求第n个正方形AnBnCnDn的边长,并求所有所作正方形的面积和Sn,并证明.
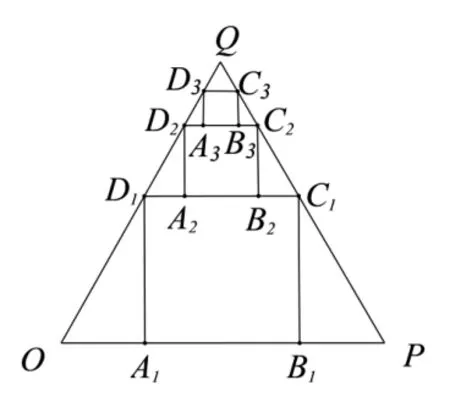
图5
3 教材例习题拓展要求
改编例习题容易,但创编例习题要适合学情、促进学生深度学习、提升学生数学核心素养就不易,需要考虑多方面要求.
首先,选题要突破重难点.教材例习题的拓展,不是题题都深掘、课课都开展;要依据教学目标,突出教学的中心任务,围绕教学重难点展开,通过对例习题的探研,让学生能够突破重难点,提升解决此类问题的能力,不应“为改编而改编”.其次,选题要典型有价值.围着知识重难点,选取的例习题要典型,要有创编的价值,不能随意拿来一道例习题就按照前文提供的路径进行创编;要挑选一些在知识网络上承上启下的、能体现知识网点的“题根”类例习题进行深度挖掘,达到“研一题、得一法、会一类”的学习效果.第三,创编难易要切合学情.创编一串问题,要以学生的学习情况和水平层次来衡量,要贴近学生最近发展区,以学生为中心,新题在内容、方法、难度、情境等方面适合学生实际需求.第四,新题内容要科学严谨.创编后的新题不能偏离课标和课本而产生偏题、怪题;不会出现常识性、科学性错误;同时表述要简洁易懂,情境要接轨现实情况、合符情理;新题要有利于学生知识生长.
同时,教师要积极转变解题教学思路,重视和用好手边的教学资源,克服“题海战术”,根据学情选择例习题进行适当的创编,激发学生对数学的探究热情,促进学生深度思考.
另外,不同课型、不同阶段习题创编挖掘应该求变存异.常规课堂教学要根据教学内容和需要,选择有价值的典型例习题,借题发挥做好教学设计对例习题进行拓展开发;高一、高二的单元综合复习课或高三的二轮复习阶段,可以选择一个主题,围绕主题选择一道例习题,或者是一道典型有价值的高考题和模拟题,对其精心设计深度挖掘,开展“一题一课”解题教学,这样教学效果更佳、对学生解题能力培养成效更显著.
———《扇形的认识》教学廖

